二次元ラプラス方程式のグリーン関数の確認

二次元ラプラシアンのグリーン関数は

\triangle G(\bm{r}) = - \delta(\bm{r}) \tag{1}

に対して，

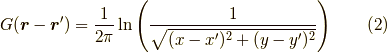
G(\bm{r}-\bm{r}^\prime) = \dfrac{1}{2 \pi } \ln \left( \dfrac{1}{\sqrt{(x-x^\prime)^2+(y-y^\prime)^2}} \right) \tag{2}

ですね．ただ，ここまでは良く本に書いてあるのですが，どう確認していいのか疑問だったので，考えてみました．

二次元のグリーン関数

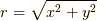まず，簡単の為，式(2)に平行移動を施して，原点で特異性を持つようにします．そして， \triangle G の面積分を原点を中心とする半径 r = \sqrt{x^2+y^2} の円盤で行った時，-1に等しいことを確認します．

まずは準備体操です．次を求めます．

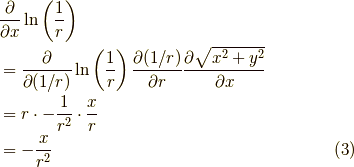
&\dfrac{\partial}{\partial x} \ln \left( \dfrac{1}{r} \right) \\&= \dfrac{\partial}{\partial(1/r)}\ln \left( \dfrac{1}{r} \right) \dfrac{\partial(1/r)}{\partial r} \dfrac{\partial \sqrt{x^2+y^2}}{\partial x} \\&= r \cdot -\dfrac{1}{r^2} \cdot \dfrac{x}{r} \\&= -\dfrac{x}{r^2} \tag{3}

よって，さらにxで偏微分すると，

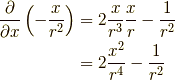
\dfrac{\partial}{\partial x} \left( -\dfrac{x}{r^2} \right) &= 2 \dfrac{x}{r^3} \dfrac{x}{r} - \dfrac{1}{r^2} \\&= 2 \dfrac{x^2}{r^4} - \dfrac{1}{r^2}

yでの偏微分も同様なので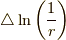， \triangle \ln \left( \dfrac{1}{r} \right) を計算してみると，

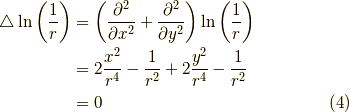
\triangle \ln \left( \dfrac{1}{r} \right) &= \left( \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial^2}{\partial y^2} \right) \ln \left( \dfrac{1}{r} \right) \\&= 2 \dfrac{x^2}{r^4} - \dfrac{1}{r^2} + 2 \dfrac{y^2}{r^4} - \dfrac{1}{r^2} \\&= 0 \tag{4}

となります．よって，グリーン関数のラプラシアンを取った結果は原点以外ではゼロに等しいことが示せました．今度は原点中心の積分を求めます．

グリーンの公式

以下でグリーンの公式を証明なしでもちいます．その公式とは，

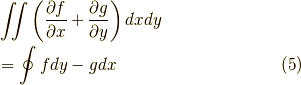
&\iint \left( \dfrac{\partial f}{\partial x} + \dfrac{\partial g}{\partial y} \right) dxdy \\&= \oint fdy - gdx \tag{5}

です．これに 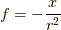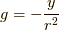f=-\dfrac{x}{r^2} , g=-\dfrac{y}{r^2} を代入したものは，積分範囲を原点中心の半径rの円として，

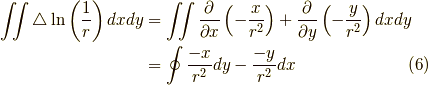
\iint \triangle \ln \left( \dfrac{1}{r} \right) dxdy &= \iint \dfrac{\partial}{\partial x} \left( -\dfrac{x}{r^2} \right) + \dfrac{\partial}{\partial y} \left( -\dfrac{y}{r^2} \right) dxdy \\&= \oint \dfrac{-x}{r^2} dy - \dfrac{-y}{r^2} dx \tag{6}

ここで，極座標を持ち出します．

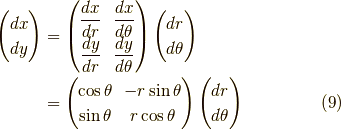
x &= r \cos \theta \tag{7} \\y &= r \sin \theta \tag{8} \begin{pmatrix} dx \\ dy \end{pmatrix} &=\begin{pmatrix}\dfrac{dx}{dr} & \dfrac{dx}{d\theta} \\\dfrac{dy}{dr} & \dfrac{dy}{d\theta}\end{pmatrix} \begin{pmatrix} dr \\ d\theta \end{pmatrix} \\&=\begin{pmatrix}\cos \theta & -r \sin \theta \\\sin \theta & r \cos \theta\end{pmatrix} \begin{pmatrix} dr \\ d\theta \end{pmatrix} \tag{9}

ですから，これらを式(6)に代入すれば，

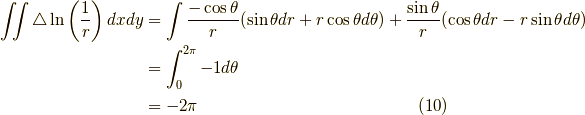
\iint \triangle \ln \left( \dfrac{1}{r} \right) dxdy &= \int \dfrac{- \cos \theta}{r} (\sin \theta dr + r \cos \theta d \theta) + \dfrac{\sin \theta}{r} (\cos \theta dr - r \sin \theta d \theta) \\&= \int_{0}^{2 \pi} -1 d \theta \\&= -2 \pi \tag{10}

となります．よって，積分範囲が原点を含むなら，

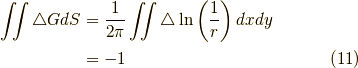
\iint \triangle G dS &= \dfrac{1}{2 \pi} \iint \triangle \ln \left( \dfrac{1}{r} \right) dxdy \\&= -1 \tag{11}

となり，確かに

\triangle G(r) = -\delta(r) \tag{12}

が確認できました．

今日はここまで．お疲れ様でした．