湯川ポテンシャルのフーリエ変換
波数 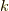 として,
として, 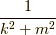 のフーリエ変換ってなんだっけ?
という所からスタートし,湯川ポテンシャルにたどり着きました.
拙記事, クーロンポテンシャルのフーリエ変換 と比べると面白いかもしれません.
のフーリエ変換ってなんだっけ?
という所からスタートし,湯川ポテンシャルにたどり着きました.
拙記事, クーロンポテンシャルのフーリエ変換 と比べると面白いかもしれません.
グリーン関数の満たす式
さて, 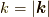 ,
, 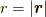 とします.
とします.

のフーリエ変換という事ですから,
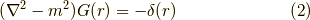
を満たすグリーン関数 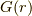 が求めたい関数だと分かります.
これから使うフーリエ変換は次とします.
が求めたい関数だと分かります.
これから使うフーリエ変換は次とします.
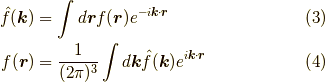
デルタ関数の積分表示は,
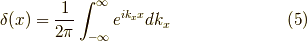
より, 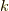 空間の全領域の積分で,
空間の全領域の積分で,
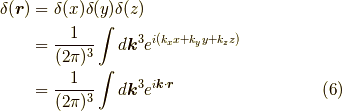
となりますから,式  は,
は,
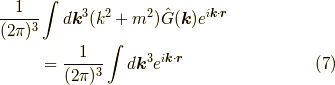
よって,

となり,これがスタートです.
フーリエ変換の実行
さて, 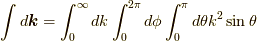 より,
より,
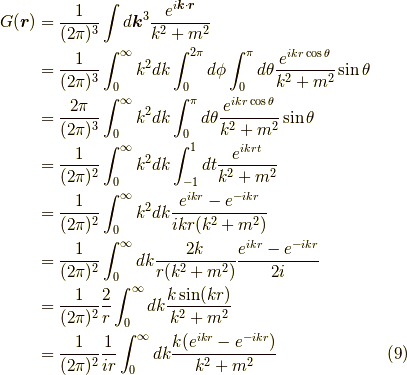
ここで, 次の 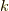 積分を求めるのに複素積分の留数定理を用います.
積分を求めるのに複素積分の留数定理を用います.
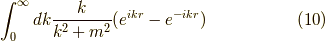
の第二項は,  と置いて,
と置いて,
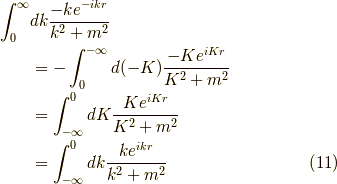
ですから,式 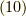 の値は
の値は

と等しくなります.
複素積分の実行

まで分かりました.これから複素積分で 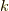 積分を実行します.
積分を実行します. 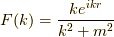 として,
として,

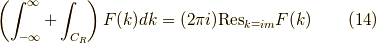
であり,ジョルダンの補題より
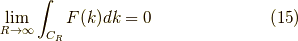
であり,留数は,
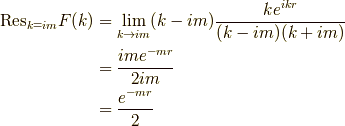
よって,
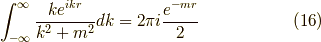
となります.これを式 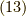 に代入して,
に代入して,
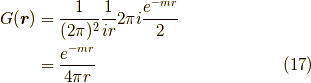
です.この指数関数的減衰をするポテンシャルは湯川ポテンシャルと言います. この計算はかなり略式ですが,以下のサイトにも導出が載っています. 場の量子論で頻出の計算英語
今回のフーリエ変換は場の量子論では知っていて当たり前の様な言い方をされることが多い気がします. 覚えておくと良いでしょう.
今日はここまで,お疲れ様でした.