収束因子を使ったフーリエ変換の拡張の例
物理学では数学的には少し怪しい操作をして, 有用な結果を得られる事があります. その一つが収束因子を使ったフーリエ変換です.
1のフーリエ変換
まずは普通にフーリエ変換をしてみましょう.
すると, ![\mathcal{F[1]}](./c55f84281ffe8fd01a486ac38a71a92b.png) は,
は,
![\mathcal{F}[1] &= \int_{-\infty}^{\infty} 1 e^{-ikx} dx \\&= \left[ \dfrac{e^{-ikx}}{-ik} \right]_{-\infty}^{\infty} \tag{1}](./6e6bebb9c6ce3bcb6620920f53281a87.png)
となります. 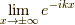 が収束しないので,
この値は定まりません.
が収束しないので,
この値は定まりません.
ここで,正の微小量 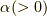 を用いて,
を用いて, 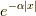 を積分核
を積分核 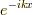 に追加して
みましょう.
に追加して
みましょう.  です.
です.
![\mathcal{F}[1] &= \lim_{\alpha \to 0} \int_{-\infty}^{\infty} 1 e^{-ikx-\alpha |x|} dx \\&= \lim_{\alpha \to 0} \int_{-\infty}^{0} 1 e^{-ikx + \alpha x} dx + \int_{0}^{\infty} 1 e^{-ikx - \alpha x} dx \\&= \lim_{\alpha \to 0} \left[ \dfrac{e^{-ikx + \alpha x}}{-ik + \alpha} \right]_{-\infty}^{0} \\&+ \lim_{\alpha \to 0} \left[ \dfrac{e^{-ikx - \alpha x}}{-ik - \alpha} \right]_{0}^{\infty} \\&= \lim_{\alpha \to 0} \dfrac{1}{-ik + \alpha} - \dfrac{1}{-ik - \alpha} \\&= \lim_{\alpha \to 0} 2\dfrac{\alpha}{k^2 + \alpha^2} \tag{2}](./3ad7494c896da1a473b7a95409df0e11.png)
ここで, 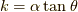 と変数変換してこれを
と変数変換してこれを 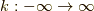 で積分すると,
で積分すると,
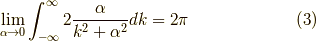
となります.ここで,式  の正体は何かと言うと,
の正体は何かと言うと, 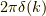 なのです.
ここで
なのです.
ここで 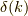 はディラックのデルタ関数です.
はディラックのデルタ関数です.
このイメージを簡単に述べておくと,積分値が  である
関数
である
関数 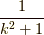 を横に微小量
を横に微小量  倍して
倍して 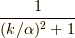 となり,
それでは曲線下の面積が
となり,
それでは曲線下の面積が  になってしまうので,
こんどは縦方向に
になってしまうので,
こんどは縦方向に 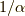 倍します.すると,
倍します.すると, 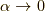 の極限で
これは
の極限で
これは 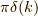 になります.つまり,
になります.つまり,
![\mathcal{F}[1] &= \lim_{\alpha \to 0} \int_{-\infty}^{\infty} e^{-ikx-\alpha |x|} dx \\&= \lim_{\alpha \to 0} 2 \dfrac{\alpha}{k^2 + \alpha^2} \\&= 2\pi \delta(k) \tag{4}](./002fadeeb65d16af23ca476d724f210c.png)
です.
xのフーリエ変換
今度は  のフーリエ変換を求めます.
今回この記事を書いた動機はこれを言いたかったからです.
のフーリエ変換を求めます.
今回この記事を書いた動機はこれを言いたかったからです.
![\mathcal{F}[x] &= \lim_{\alpha \to 0} \int_{-\infty}^{\infty} x e^{-ikx-\alpha |x|} dx \\&= \lim_{\alpha \to 0} \int_{-\infty}^{0} x e^{-ikx + \alpha x} dx + \int_{0}^{\infty} x e^{-ikx - \alpha x} dx \\&= \lim_{\alpha \to 0} \left[ \dfrac{xe^{-ikx + \alpha x}}{-ik + \alpha} \right]_{-\infty}^{0} \\&+ \lim_{\alpha \to 0} \left[ \dfrac{xe^{-ikx - \alpha x}}{-ik - \alpha} \right]_{0}^{\infty} \\&- \int_{-\infty}^{0} \dfrac{e^{-ikx + \alpha x}}{-ik + \alpha} dx \\ &- \int_{0}^{\infty} \dfrac{e^{-ikx - \alpha x}}{-ik + \alpha} dx \\&= \lim_{\alpha \to 0} \dfrac{-1}{(-ik+\alpha)^2} + \dfrac{1}{(-ik-\alpha)^2} \\&= \lim_{\alpha \to 0} \dfrac{-4i \alpha k}{(k^2 + \alpha^2)^2} \tag{5}](./6275c7f17b84fcd4f499f68c8e7aafd8.png)
これは奇関数です.よって単純に積分してもゼロになります. 原点に局在する奇関数,何かピンときませんか?
そうです.これは 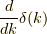 に関係します.
に関係します.
![\dfrac{d}{dk}(2 \pi \delta(k)) &= \lim_{\alpha \to 0} 2 \dfrac{d}{dk}\left( \dfrac{\alpha}{k^2+\alpha^2} \right) \\&= \lim_{\alpha \to 0} 2 \dfrac{-2k \alpha}{(k^2+\alpha^2)^2} \\&= \lim_{\alpha \to 0} \dfrac{-4 \alpha k}{(k^2 + \alpha^2)^2} \\&= (1/i) \mathcal{F}[x]](./248aadaed628cf32e64b6847c4cb347e.png)
よって,
![\mathcal{F}[x] = 2 \pi i \dfrac{d \delta(k)}{dk}](./a8132638ff67f022acbcde740ff01f61.png)
と云う訳です.これは 超関数の意味 での  のフーリエ変換に一致していますね.
のフーリエ変換に一致していますね.
それでは今日はこの辺で,お疲れ様でした.