一般化されたエルミート多項式
この記事では,エルミート多項式を一般化します. 色々,遊んでいます.
準備
いきなりですが,次の演算子の変形ができます.
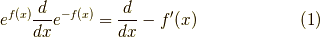
証明はフーリエ変換を使います.
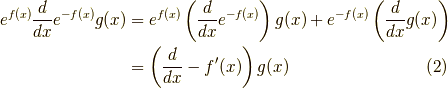
で, 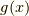 は任意ですから,
は任意ですから,
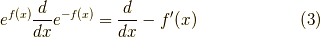
が言えました.さらには,
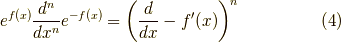
も自明です.
エルミート多項式
式 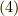 の演算子を
の演算子を 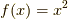 ,
, 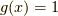 とし,調整の為
とし,調整の為 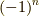 を掛けると,
を掛けると,
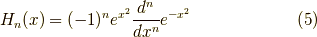
が得られ,また,
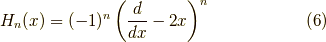
も出ます.式 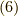 は変形して,漸化式,
は変形して,漸化式,
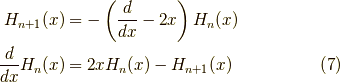
が得られます.
エルミート多項式の拡張
と言うことはです. 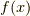 と
と 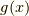 に好きな関数を入れてやれば,
エルミート多項式の拡張が容易に得られます.
に好きな関数を入れてやれば,
エルミート多項式の拡張が容易に得られます.
単純に 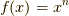 ,
, 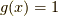 が直接的な拡張と言えるでしょう.
が直接的な拡張と言えるでしょう.
僕が気に入っているのは, 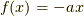 ,
, 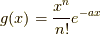 の時で,
これは
の時で,
これは 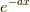 を無視して,
を無視して, 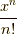 部分だけを微分する計算になります.
部分だけを微分する計算になります.
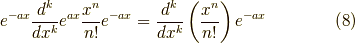
であり,
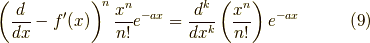
となります.
コメントをしておくと,僕は最初,線形代数のジョルダン標準形で出てくる,冪ゼロ因子の,
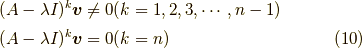
のアナロジー 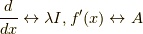 として,これを発見しました.
何か,面白い事が言えそうだと思っています.
として,これを発見しました.
何か,面白い事が言えそうだと思っています.
今日はここまで,お疲れさまでした!!