フーリエ変換の実例
この記事では,フーリエ変換, フーリエ逆変換の実例について書いてみました.
フーリエ変換
これから
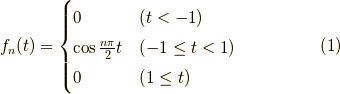
(ただし  は非負の整数)の
フーリエ変換を求めます.その前に関数の形を確認しておきましょう.
は非負の整数)の
フーリエ変換を求めます.その前に関数の形を確認しておきましょう.
フーリエ変換の公式は,
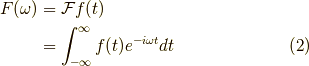
フーリエ逆変換もついでに書いておくと,
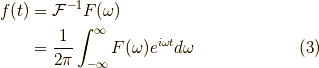
です.
さっそく,フーリエ変換を考えてみましょう.簡単の為, 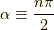 としておきます.
としておきます.
![F_n(\omega) &= \mathcal{F}f_n(t) \\&= \int^\infty_{-\infty} f(t) e^{-i \omega t} dt \\&= \int^1_{-1} \cos (\frac{n \pi}{2} t) e^{-i \omega t} dt \\&= \int^1_{-1} \frac{1}{2} (e^{i \alpha t}+ e^{-i \alpha t} )e^{-i\omega t} dt \\&= \frac{1}{2} \int^1_{-1} e^{i (\alpha - \omega)t}+e^{-i(\alpha + \omega)t} dt \\&= \frac{1}{2}\big[\frac{e^{i(\alpha -\omega)t}}{i(\alpha-\omega)}-\frac{e^{-i(\alpha +\omega)t}}{i(\alpha+\omega)} \big]^1_{-1} \\&= \frac{1}{2i} \big[ \frac{(\alpha+ \omega)e^{i(\alpha - \omega)t}-(\alpha- \omega)e^{-i(\alpha + \omega)t}}{\alpha^2 - \omega^2} \big]^1_{-1} \\&= \frac{1}{2i(\alpha^2 - \omega^2)} \big\{ (\alpha+\omega) \big( e^{i(\alpha-\omega)} - e^{-i(\alpha -\omega)} \big) - (\alpha - \omega)\big( e^{-i(\alpha + \omega)} - e^{i(\alpha + \omega)} \big) \big\} \\&= \frac{1}{\alpha^2-\omega^2} \big\{ (\alpha + \omega)\frac{e^{i(\alpha-\omega)}-e^{-i(\alpha -\omega)}}{2i}+(\alpha-\omega)\frac{e^{i(\alpha+\omega)}-e^{-i(\alpha+\omega)}}{2i} \big\} \\&= \frac{1}{\alpha^2-\omega^2} \big\{ ( \alpha + \omega )\sin(\alpha - \omega ) +(\alpha-\omega) \sin( \alpha + \omega ) \big\} \\&= \frac{1}{\alpha^2-\omega^2} \big\{ \alpha (\sin (\alpha -\omega )+\sin (\alpha + \omega )) + \omega ( \sin (\alpha - \omega)- \sin (\alpha + \omega) ) \big\} \\&= \frac{1}{\alpha^2-\omega^2} \big( 2 \alpha \sin \alpha \cos \omega -2 \omega \cos \alpha \sin \omega \big) \\&= \frac{1}{ (\frac{n \pi}{2})^2 - \omega^2 } \big( n \pi \sin \frac{n \pi }{2} \cos \omega - 2 \omega \cos \frac{n \pi }{2} \sin \omega \big) \tag{4}](./034287edad0aa3d86b7a800929a13fe3.png)
ここで, 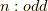 を
を  が奇数の時,
が奇数の時,  を
を  が偶数の時とすると,
が偶数の時とすると,
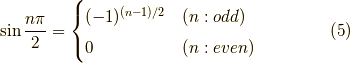
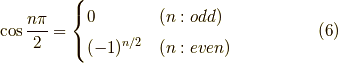
なので,
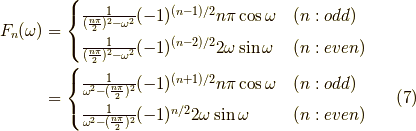
となりました.これが,関数  のフーリエ変換
です.
のフーリエ変換
です. 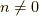 の時は,
の時は, 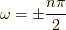 で極(分母がゼロになり,発散すること)が出てきそう
ですが,
で極(分母がゼロになり,発散すること)が出てきそう
ですが, 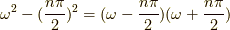 というように一次の極なのと,
ちょうど,そこでサインないしコサインが一次の零点をもつので,これは,除去可能な特異点です.
よって,そこでは緩やかなピークを持ちます.
実は,
というように一次の極なのと,
ちょうど,そこでサインないしコサインが一次の零点をもつので,これは,除去可能な特異点です.
よって,そこでは緩やかなピークを持ちます.
実は, 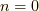 の時の
の時の  も除去可能な特異点です.(
も除去可能な特異点です.( 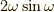 が二次の零点のため,分母が2次の極を持つが,やはり除去可能な特異点となる.)
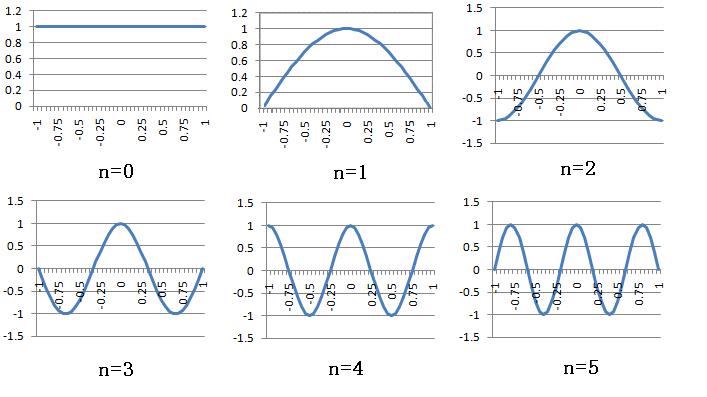
下にフーリエ変換したもののグラフを書きます.
横軸は,
が二次の零点のため,分母が2次の極を持つが,やはり除去可能な特異点となる.)
下にフーリエ変換したもののグラフを書きます.
横軸は,  です.
です.

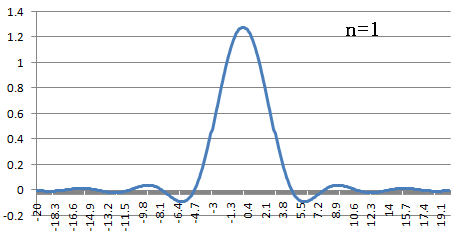
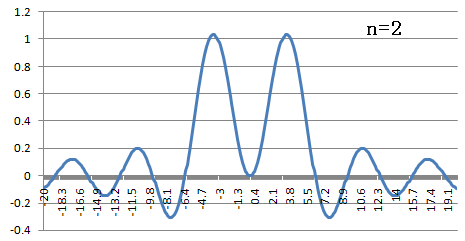
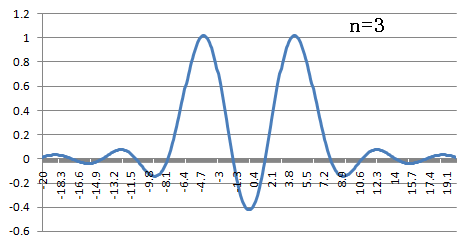
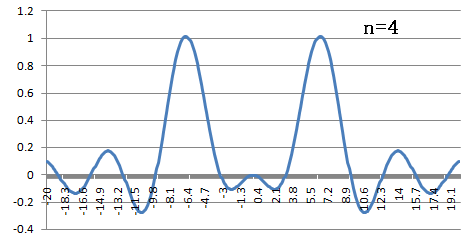
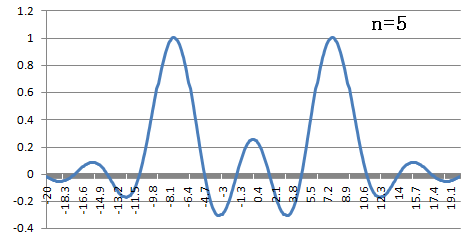
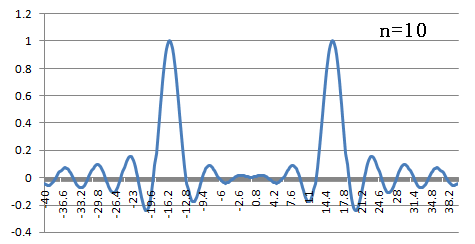
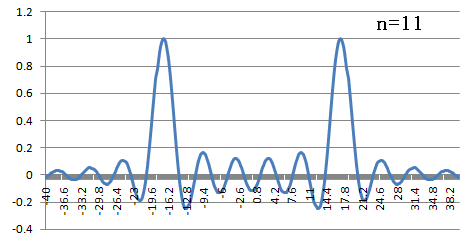
フーリエ逆変換(nが奇数の時)
さて,フーリエ変換ができたところで,フーリエ逆変換を行い,元に戻るか見てみましょう.
複素関数の積分法を必要とします.
まず,  が奇数のとき,かつ,
が奇数のとき,かつ, 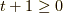 つまり,
つまり, 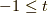 の時 [*] を積分してみます.
の時 [*] を積分してみます.
| [*] | t+1 がゼロ以上という条件は,後述の式 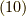 の指数関数の指数 の指数関数の指数 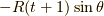 が複素平面の上半面で負になり,積分路 が複素平面の上半面で負になり,積分路 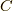 での積分がゼロになるように選びました. での積分がゼロになるように選びました. |
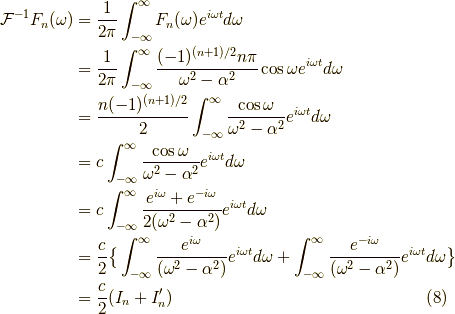
ただし,  と
しました.
と
しました.  は下図のような積分路をとれば求められます.
は下図のような積分路をとれば求められます.

積分路が囲む領域に特異点がないので,以下の様な積分となります.
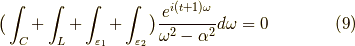
ここで積分路  を計算します.
を計算します.  と置くと,
と置くと,  となるから,
となるから,
![\big| \int_C \frac{e^{i(t+1)\omega}}{\omega^2-\alpha^2} d \omega \big| &= \big| \int_0^\pi \frac{e^{i(1+t)R(\cos \theta + i \sin \theta)}}{R^2 e^{2i\theta} - \alpha^2}iR e^{i \theta} d \theta \big| \\&< \frac{R}{R^2 -\alpha^2} \int_0^\pi e^{-R(t+1)\sin \theta} d\theta \\&< \frac{R}{R^2 -\alpha^2} \int_0^\pi e^{-2R(t+1)\theta /\pi} d\theta \\&< \frac{R}{R^2 -\alpha^2} \big[ \frac{-\pi}{2R(t+1)} e^{-2R(t+1)\theta/\pi} \big]_0^\pi \\&= \frac{\pi}{2(t+1)(R^2 -\alpha^2)} (1-e^{-2 R(1+t)} ) \\&\stackrel{R \to \infty}{\to} 0 \tag{10}](./3ab2651fb8d8144f1d96536d1a857c86.png)
一行目から二行目は,位相部分を無視して,分母は最小になるように展開しました.
二行目から三行目は,下図の様に 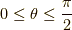 において,
において, 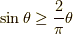 となる
ことを利用しました.
となる
ことを利用しました.
積分路  については,その留数に時計回りなのでマイナスが掛かって,
更に半周しかしないので
については,その留数に時計回りなのでマイナスが掛かって,
更に半周しかしないので  ではなく
ではなく  が掛かって,
が掛かって,
![\int_{\varepsilon_1} \frac{e^{i(t+1)\omega}}{\omega^2-\alpha^2} d\omega &= -i \pi \mathrm{Res}_{\omega \to \alpha} \big[ \frac{e^{i(t+1)\omega}}{\omega^2 -\alpha^2} \big] \\&= -i \pi \mathrm{lim}_{\omega \to \alpha} (\omega-\alpha) \frac{e^{i(1+t)\omega}}{(\omega-\alpha)(\omega + \alpha)} \\&= -i \pi \frac{e^{i(1+t)\alpha}}{2 \alpha} \tag{11}](./ac3fc6099ef5c874e3319a716b180913.png)
積分路 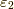 についても同様に,
についても同様に,
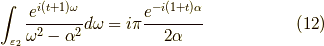
よって,
となります.これはつまり, 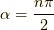
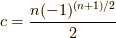 でしたから,
でしたから,

次に行きましょう.
次は,  が奇数,かつ,
が奇数,かつ, 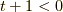 つまり,
つまり, 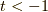 の時です.
積分路は,無限遠の半円について,
の時です.
積分路は,無限遠の半円について,  の指数が負になる領域
の指数が負になる領域 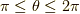 より,
下半面(下図参照)になります.
より,
下半面(下図参照)になります.
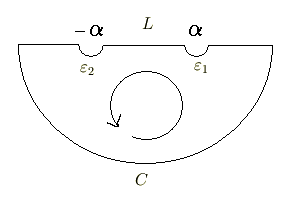
これは留数の積分方向は変わらず,積分路 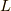 の向きだけが変わるので,
の向きだけが変わるので,

となります.よって,まとめると,
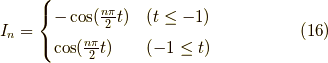
今求めたのは
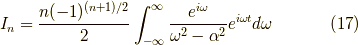
でしたが,一方,
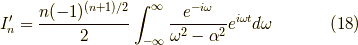
も求めないと,

は求まりません.よって,求めます.  が奇数,かつ
が奇数,かつ  ,つまり,
,つまり,  の時,積分路は下図のようになって,
の時,積分路は下図のようになって,

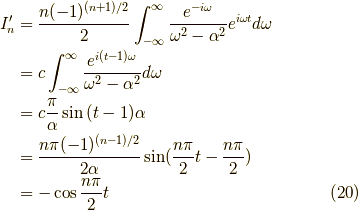
さっきと同様に,  が奇数,かつ
が奇数,かつ 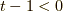 ,つまり,
,つまり, 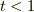 の時,積分路は下図のようになり,
式
の時,積分路は下図のようになり,
式 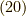 とは,符号が変わるので,
とは,符号が変わるので,


つまり,
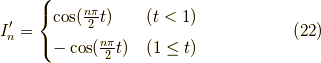
よって,まとめると下図のようになります.
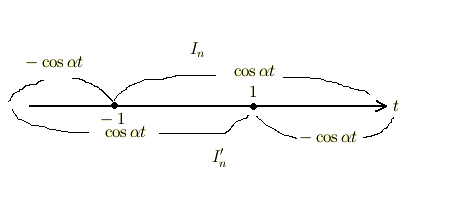
つまり,
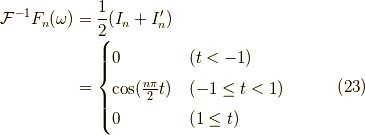
ふぅ,これで逆変換の内,  が奇数の時を求めることができました.
次は偶数の時です,頑張りましょう.
が奇数の時を求めることができました.
次は偶数の時です,頑張りましょう.
フーリエ逆変換(nが偶数の時)
さて,  が偶数,かつ
が偶数,かつ  の時,
の時,  のフーリエ変換は,
のフーリエ変換は,
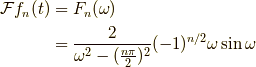
でした.今求めたいのは,  と置いて,
と置いて,
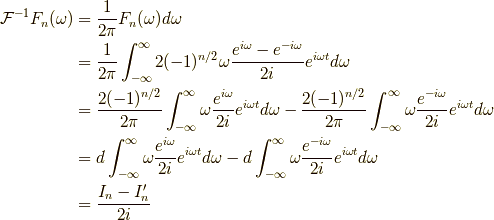
まず,  を求めましょう.
を求めましょう.
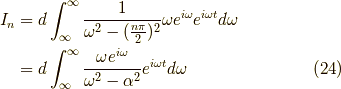
となります. 下図のように積分路を取ると,

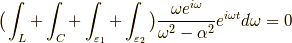
となります.まず,積分路  を評価します.
を評価します.  と置けば,
と置けば,  より,
より,

積分路 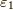 について,前と同じく時計回りで半周することから留数に
について,前と同じく時計回りで半周することから留数に  を掛けたものが,積分値となります.
を掛けたものが,積分値となります.

同様に,積分路  も求めると,
も求めると,

よって,
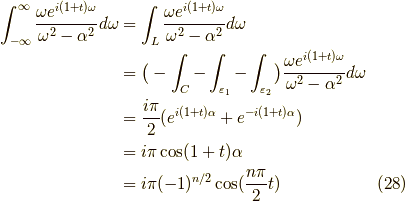
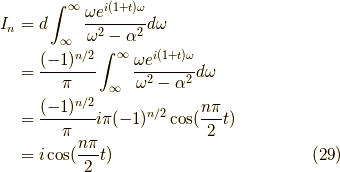
となります.同様に,  が偶数,かつ
が偶数,かつ  の時,積分路は下図のようになります.
の時,積分路は下図のようになります.

ここでも,留数の積分方向は変わらず,積分路 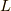 の向きが変わるので,
の向きが変わるので,

よって,まとめると,
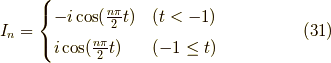
次に,  が偶数,かつ,
が偶数,かつ, 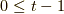 つまり
つまり 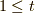 の時,
の時, 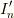 を求めます.
を求めます.  として,
積分路は下図のようになり,
として,
積分路は下図のようになり,

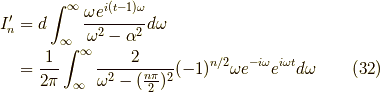
を考えます.
これが最後ですので,安心してください.
これは,式 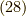 の下から二行目の
の下から二行目の 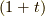 を
を  で置き換えたものに等しいので,
で置き換えたものに等しいので,
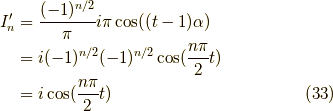
同様に,  が偶数の時,かつ,
が偶数の時,かつ, 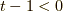 つまり
つまり 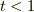 の時,
積分路は下図のようになって,積分路
の時,
積分路は下図のようになって,積分路 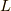 の向きが反転するので,
の向きが反転するので,

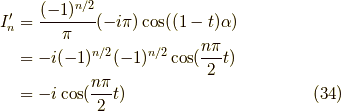
よって,まとめると,
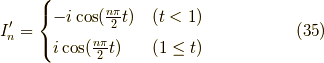
となります.いよいよ最後の仕上げです. 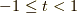 の時,
の時,
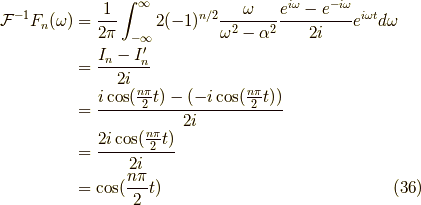
さらに, 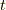 が
が 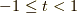 以外の時は,
以外の時は, 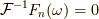 となるので,
まとめると(下図も参照のこと),
となるので,
まとめると(下図も参照のこと),

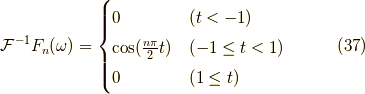
よって,ついに今回の例において,ある関数  のフーリエ変換
のフーリエ変換 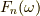 のフーリエ逆変換が,
元の関数
のフーリエ逆変換が,
元の関数 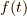 に等しいことが分かりました.
今日はこの辺で,それでは.
に等しいことが分かりました.
今日はこの辺で,それでは.
追記(2014/11/13):逆変換の積分を正確に書くには「コーシーの主値積分」を用いるようです.僕は詳しくないので, 他を当たってみてください(^^;).
ちなみに式 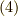 の下から4行目を見ると,その式は,
の下から4行目を見ると,その式は,

となります.
なんと,これはシンク関数を平行移動したものを重ね合わせたものです.
( 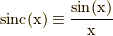 をシンク関数と言います.)
しかも,
をシンク関数と言います.)
しかも,  ,つまり,
,つまり,  は実数値を取ることができます.
これは今回の周波数空間のグラフは,ピークを持つ波が二つずれて重ねあわされた
グラフとなっていることを示しています.
は実数値を取ることができます.
これは今回の周波数空間のグラフは,ピークを持つ波が二つずれて重ねあわされた
グラフとなっていることを示しています.