クーロンポテンシャルのフーリエ変換
結構,有名な積分だと思います. ときどき解法を忘れてしまうので,自分用にメモです.
問題の積分は,
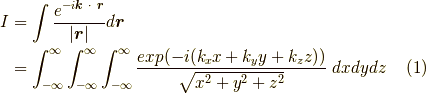
式 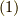 の第二行を見るとなんとも物騒な積分ですが,この積分は次の極座標を用いれば簡単になります.
の第二行を見るとなんとも物騒な積分ですが,この積分は次の極座標を用いれば簡単になります.
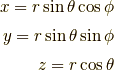
ちなみに 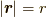 です.一応初めての方もいらっしゃると思うので,
この変換のヤコビアン(ヤコビの行列式:積分の微小体積要素の変換式)は,お馴染み(?)の
です.一応初めての方もいらっしゃると思うので,
この変換のヤコビアン(ヤコビの行列式:積分の微小体積要素の変換式)は,お馴染み(?)の
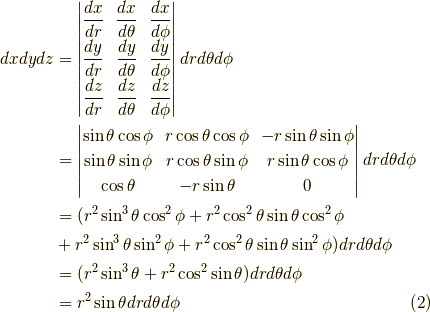
です.よって,  と
と  が
が  の角を成すとして,
うまく座標系の取り方を工夫して,
の角を成すとして,
うまく座標系の取り方を工夫して,  を
を  方向を向いたベクトルとすれば,
方向を向いたベクトルとすれば,
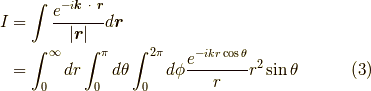
ここで, 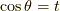 ,
, 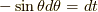 と変数変換すると,
と変数変換すると,
![I &= \int \dfrac{e^{-i\bm{k} \ \cdot \ \bm{r}}}{|\bm{r}|} d \bm{r} \\&= \int_{0}^\infty dr \int_0^{2\pi}d \phi \left( \int_{-1}^{1} r e^{- i k r t} dt \right) \\&= \int_{0}^\infty dr \int_0^{2\pi}d \phi \left[ r \frac{e^{- i k r t} }{-ikr} \right]_{-1}^{1} \\&= \int_{0}^\infty dr \int_0^{2\pi}d \phi \left[ \frac{e^{- i k r t} }{ik} \right]_{1}^{-1} \\&= \int_{0}^\infty dr \int_0^{2\pi}d \phi \dfrac{1}{ik} \left( e^{i k r } - e^{- i k r } \right) \\&= \int_{0}^\infty dr \int_0^{2\pi}d \phi \dfrac{2}{k} \sin (kr) \tag{4}](./ef0efd24e15e482e1cef0f8f00b58e7d.png)
ここでいかにも物理(not数学的な意味で)らしい手法を
用います. 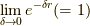 を被積分関数に掛けるのです.
すると,無限遠での値が収束し,
を被積分関数に掛けるのです.
すると,無限遠での値が収束し,
![I &= \lim_{\delta \to 0} \int_{0}^\infty dr \int_0^{2\pi}d \phi \dfrac{1}{ik} e^{-\delta r} (e^{i kr} - e^{-ikr}) \\&= \int_0^{2 \pi} d \phi \dfrac{1}{ik} \lim_{\delta \to 0} \left[ \dfrac{e^{(ik-\delta)r}}{ik-\delta} - \dfrac{e^{(-ik-\delta)r}}{-ik-\delta} \right]_{0}^{\infty} \\&= \int_0^{2 \pi} d \phi \dfrac{1}{ik} \lim_{\delta \to 0} \left[ \dfrac{ 0-1 }{ik-\delta} + \dfrac{ 0-1 }{ik+\delta} \right] \\&= \int_0^{2 \pi} d \phi \dfrac{1}{ik} \left( \dfrac{-2}{ik} \right) \\&= \int_0^{2 \pi} d \phi \dfrac{2}{k^2} \\&= \dfrac{4 \pi}{k^2} \tag{5}](./4d774aad65c5911b696018918c768933.png)
となります.よって,
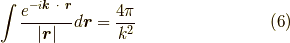
が言えました.
それでは今日はこの辺で,お疲れ様でした.