フーリエ級数
ベクトル空間では,一次独立な基底をつかって,任意のベクトルを表すことができます.関数についても,一次独立な関数の集まりを使えば,ひとつの関数を表すことができるんです( 直交関数系 参照).今回は,この「一次独立な関数の集まり(関数列)」が直交関数系である,三角関数であったときの場合をご紹介します.
フーリエ級数
準備
この記事では,簡単のために  を実関数として話を進めていきます.複素関数について考えるときは,実部と虚部について同じ手順で計算すればいいだけだからです.
を実関数として話を進めていきます.複素関数について考えるときは,実部と虚部について同じ手順で計算すればいいだけだからです.
まず,思い出してください.直交関数系の「直交関数系から」というセクションで,チラッと見たように,正規直交関数系 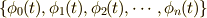 とある関数
とある関数  との相関を取った結果は,
との相関を取った結果は,  を
を 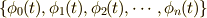 の各元に分解したときにつく係数がでてきてくれるはずです.今,この正規直交関数系が三角関数だった場合での係数を求めてみましょう!
の各元に分解したときにつく係数がでてきてくれるはずです.今,この正規直交関数系が三角関数だった場合での係数を求めてみましょう!
| [*] | 正規直交関数系の定義を忘れた方は, 直交関数系 を見てください. |
計算しみよう!
関数  が周期
が周期 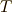 を持つとき(すなわち,
を持つとき(すなわち, 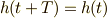 が成り立つとき),
が成り立つとき),  が持つ最大の周期は
が持つ最大の周期は 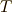 であるということがいえます.
であるということがいえます.
なので,この関数に関しては, 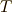 以上の周期成分を考える必要はありません.だから,
以上の周期成分を考える必要はありません.だから,  を三角関数で表す場合も,
を三角関数で表す場合も, 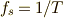 より小さい周波数成分を考慮する必要はありません.
より小さい周波数成分を考慮する必要はありません.
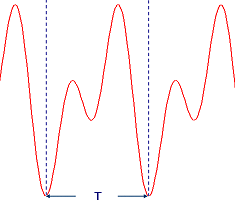
ここで,相関を取るのは一定な間隔 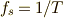 ずつ離れている周波数
ずつ離れている周波数 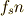 での波です.この関数に対する,範囲
での波です.この関数に対する,範囲 ![[-T/2<t<T/2]](./df11a59c46f028e6045018d10ac8762d.png) での,正規直交関数系を使った相関関数を計算するために,
での,正規直交関数系を使った相関関数を計算するために,  と同じように,最大周期
と同じように,最大周期 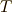 であるような正規直交関数系を用意する必要があります.
であるような正規直交関数系を用意する必要があります.
まず,用意すべき直交関数系を考えると・・・

この関数列は互いに直交しています.相関を取ってみて,以下で確認しましょう!
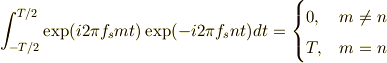
| [†] | 複素関数の相関を取るとき(関数の内積を求めるとき)は,その値(ノルム)が実数になってほしいので,相手の関数は共役なものを使います.今の場合, 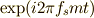 の相関を取るのは, の相関を取るのは, 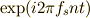 の共役である の共役である 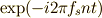 となります. となります. |
さて,上の計算結果からさらに,この関数列を正規直交関数系にするために,関数列に 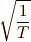 を掛けておく必要があると分かりますね.しかし,このままでは
を掛けておく必要があると分かりますね.しかし,このままでは  と関数列の相関をとったときに,あまり綺麗な形になりません.ここでは最後に二つの関数の相関を取ったときに
と関数列の相関をとったときに,あまり綺麗な形になりません.ここでは最後に二つの関数の相関を取ったときに 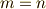 での値が
での値が 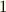 になることだけが重要なのですから,
になることだけが重要なのですから,  と相関を取る関数列を
と相関を取る関数列を 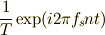 とし,その結果,
とし,その結果,  を
を 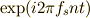 に分解したときにつく係数が求められると考えても,本質は何も変わりません.
に分解したときにつく係数が求められると考えても,本質は何も変わりません.
このことから,  と相関を取る関数列を以下のようにしておきましょう!
と相関を取る関数列を以下のようにしておきましょう!
![\Biggl[ \frac{1}{T}, \frac{1}{T}\exp(i2\pi f_s t),\frac{1}{T}\exp(i4\pi f_s t),\cdots,\frac{1}{T}\exp(i2\pi f_s n t),\cdots \Biggr]](./fca128d69912133ea733d7a89a529731.png)
関数列を用意できましたので,さっそく  との相関を取ってみましょう.
との相関を取ってみましょう.
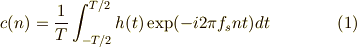
| [‡] |  は は 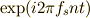 に分解されることを考え, に分解されることを考え, 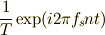 ではなくて,その複素共役である ではなくて,その複素共役である 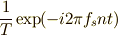 で相関を取っていることに注意しましょう. で相関を取っていることに注意しましょう. |
相関を取ると,  を
を 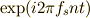 に分解したときの係数が現れるのでしたね.なので,以下の表現が可能になると考えられます.
に分解したときの係数が現れるのでしたね.なので,以下の表現が可能になると考えられます.
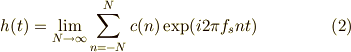
さらに,オイラーの公式 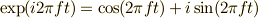 を使って,
を使って, 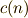 を実部と虚部に分けて考えて見ましょう.
を実部と虚部に分けて考えて見ましょう.
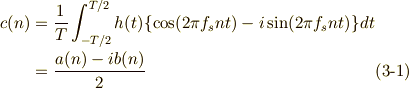
ここで,
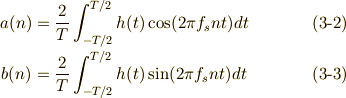
とおきますここで,式(3)から, 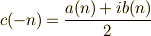 であることを利用すると,,
であることを利用すると,,
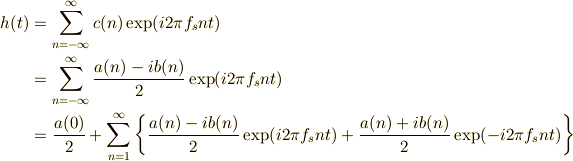
上のように書くことが出来ます.この式を 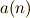 や
や 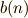 について整理すると,
について整理すると,
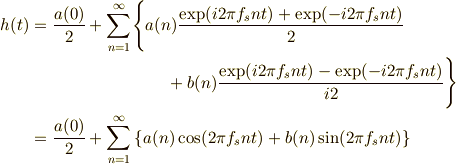
やっと,  を三角関数に分解した形にたどり着きました!!
を三角関数に分解した形にたどり着きました!!
| [§] | 実は 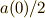 は は  の周期 の周期 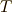 における,平均値となっています.これは,上式を理解するうえで重要なことです.上式を眺めて確認してみてください. における,平均値となっています.これは,上式を理解するうえで重要なことです.上式を眺めて確認してみてください. |
まとめ
このように有限の周期を持つ関数  を
を 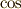 や
や  の無限級数の形で表すとき,この無限級数を フーリエ級数 といい,
の無限級数の形で表すとき,この無限級数を フーリエ級数 といい, 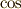 や
や  についている係数
についている係数 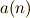 ,
, 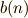 を フーリエ係数 といいます.
を フーリエ係数 といいます.
さらに, 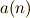 ,
, 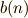 の前に出てきた
の前に出てきた 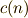 は 複素フーリエ係数 という名前がついています.同じく,
は 複素フーリエ係数 という名前がついています.同じく, 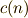 で表される無限級数の式(2)は 複素フーリエ級数 といいます.
で表される無限級数の式(2)は 複素フーリエ級数 といいます.
また,関数のフーリエ係数を求めることを フーリエ級数展開 といいます.
フーリエ級数から,フーリエ変換へ!
ここまでは,ある周期を持った関数について,考えてきました.しかし,世の中,そんな周期関数ばかりなわけがありません.そんな非周期関数については,このフーリエ級数,フーリエ級数展開はどうなってしまうのでしょうか!?
百聞は一見に如かず.実際に,有限だった周期を 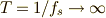 とすることで,非周期関数の複素フーリエ級数を求めてみましょう.
とすることで,非周期関数の複素フーリエ級数を求めてみましょう.
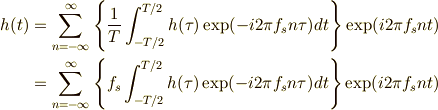
この式で, 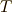 を十分に大きくしていくと,
を十分に大きくしていくと, 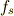 はどんどん小さくなって,
はどんどん小さくなって,  と書くことができます.
と書くことができます.
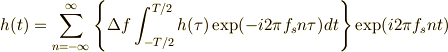
さらにここで,この微小な 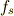 が
が 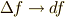 となると考えると,
となると考えると, 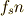 も
も 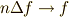 となります.これの意味するところは,
となります.これの意味するところは, 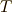 を大きくしたことによって,離散的だった周波数変数の間隔
を大きくしたことによって,離散的だった周波数変数の間隔 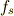 が十分に小さくなり,全ての
が十分に小さくなり,全ての 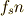 が連続の周波数変数
が連続の周波数変数 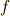 とみなせるということです.周波数変数が連続的になるので,級数をとっていた
とみなせるということです.周波数変数が連続的になるので,級数をとっていた  も積分の
も積分の 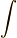 の形になります.また,
の形になります.また, 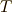 が十分に大きいのですから,
が十分に大きいのですから, 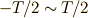 だった積分の範囲も
だった積分の範囲も 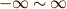 となります.
となります.
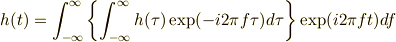
なるほど!上の式から, 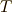 と
と 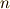 の極限をとることで,
の極限をとることで,
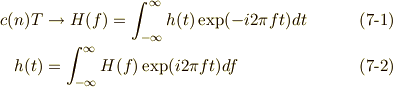
という式になることが分かります.
そしてそして,,ご存知の方はご存知のはず.式(7-1)こそ, フーリエ変換 の定義 [*] なのです!!式(7-2)はフーリエ逆変換の定義になっています.すなわち,非周期関数のフーリエ級数を無理やり求めようとすると,行き着く先はフーリエ変換になるということです.
| [¶] | フーリエ変換の定義には何通りかあります.詳しくは フーリエ変換の第一歩 をご覧ください. |