フーリエ変換の三連続積と畳み込み積分の拡張
以前, 相関関数と畳み込み積分のフーリエ変換 でフーリエ変換の2つの積は,畳み込み積分になる ことを学びましたが,それでは,3つの積はどうなるのでしょうか.短い記事です.
結論から言います.フーリエ変換すると3つの積になる関数は,
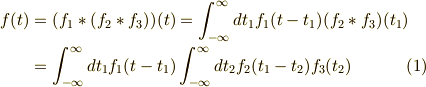
という関数です.確かめてみましょう.上の式をフーリエ変換してみます.
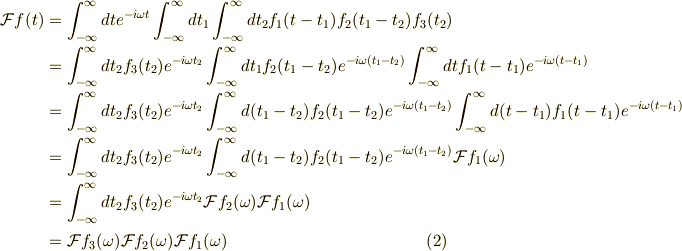
以上,今日はここまで.お疲れ様でした.
以前, 相関関数と畳み込み積分のフーリエ変換 でフーリエ変換の2つの積は,畳み込み積分になる ことを学びましたが,それでは,3つの積はどうなるのでしょうか.短い記事です.
結論から言います.フーリエ変換すると3つの積になる関数は,
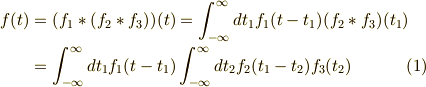
という関数です.確かめてみましょう.上の式をフーリエ変換してみます.
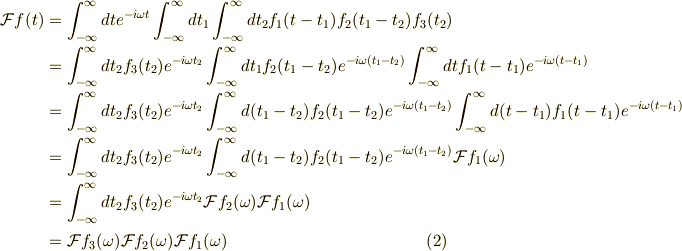
以上,今日はここまで.お疲れ様でした.