流体力学における最小作用の原理(提案)
本記事では, 流体力学, より一般的には, 流体や弾性体を含む連続体力学の基礎方程式であるコーシーの運動方程式(Cauchy's equation)について, 従来は力のつり合いから直接与えられてきたものを, 最小作用の原理あるいは変分原理の枠組みの中で導出する具体的な方法を提案したいと思います.
1.コーシーの運動方程式
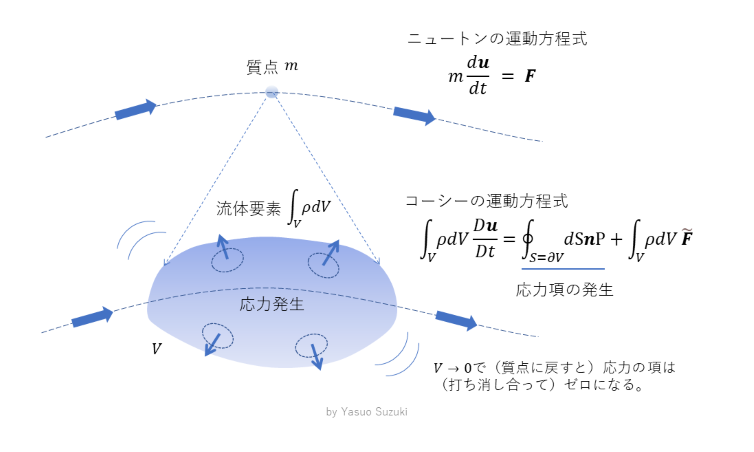
コーシーの運動方程式というのは, 任意の連続体において運動量の輸送を記述する基本的な式です. この方程式は, 質点に関するニュートンの運動方程式(Newton's equation)における質点を,広がりのある流体要素に拡張したものであるとみなすことができます. 流体要素はある体積を持ち, 変形しながら流れていきます. そして, 流体要素の表面の各点は周囲に対し応力を作用しますので, その項(接触力の項)がニュートンの運動方程式に加わることになります. まずは両方程式をじっと見比べてみてください.
1.1 ニュートンの運動方程式

ここで, 質点の質量,速度をそれぞれ  ,
, 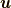 , 時刻(時間)を
, 時刻(時間)を 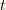 , 外力を
, 外力を 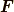 としています.
としています.
1.2 コーシーの運動方程式
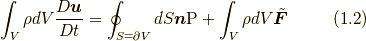
ここで,流体要素の体積, 表面積をそれぞれ 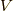 ,
, 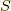 , 各点の密度, 速度を
, 各点の密度, 速度を 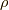 ,
, 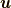 , 表面のある点から外に向かう単位法線ベクトル, その点で外にはたらく応力(正確には応力テンソル)をそれぞれ
, 表面のある点から外に向かう単位法線ベクトル, その点で外にはたらく応力(正確には応力テンソル)をそれぞれ 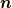 ,
, 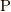 , 単位質量あたりにはたらく外力(体積力)を
, 単位質量あたりにはたらく外力(体積力)を 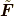 ,
, 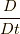 は,
は, 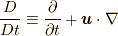 でラグランジュ微分(Lagrangian derivative)あるいは物質微分(material derivative)などと呼ばれる作用素です.
でラグランジュ微分(Lagrangian derivative)あるいは物質微分(material derivative)などと呼ばれる作用素です. 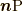 の意味は式(4.6)参照を参照ください. なお, 後述しますが, 本稿ではすべての物理量を場の量として扱います.
の意味は式(4.6)参照を参照ください. なお, 後述しますが, 本稿ではすべての物理量を場の量として扱います.
2.ニュートンの運動方程式の導出
まず,ニュートンの運動方程式の導出のポイントだけ復習してみましょう.議論の展開上, 何が変数であり, 何がそうでないかが重要になってくるため, 以降しばらく, 変数を極力省略せずに書きます.
2.1 作用
作用 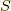 は以下で定義されます.
は以下で定義されます.
![S \left[ \bm{x} \right] \equiv \int dt m \tilde{\mathcal{L}} \left( \bm{x}(t), \frac{d \bm{x}(t)}{dt} \right) = \int dt m \left( \frac{1}{2} \left( \frac{d \bm{x}(t)}{dt} \right)^{2} - \tilde{U}(\bm{x}(t)) \right) \tag{2.1}](./86335bceb7c3ff65bf4e8febedcc5dce.png)
ここで, 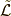 はラグランジアン密度であり, 質点の位置ベクトル, 単位質量あたりのポテンシャルエネルギーをそれぞれ
はラグランジアン密度であり, 質点の位置ベクトル, 単位質量あたりのポテンシャルエネルギーをそれぞれ 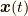 ,
, 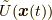 としています. 作用
としています. 作用 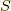 は,
は, 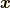 の汎関数です.
の汎関数です.
ラグランジアン密度 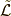 を書きだすと,
を書きだすと,
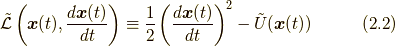
です.
2.2 最小作用の原理
作用(2.1)について, 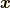 による変分
による変分 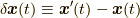 を行い, 部分積分を行い, 全微分の項を境界条件により除いて整理すると,
を行い, 部分積分を行い, 全微分の項を境界条件により除いて整理すると,
![\delta S \left[ \bm{x} \right] = \int dt m \left( -\frac{d^{2}\bm{x}(t)}{dt^{2}}+\tilde{F}(\bm{x}(t)) \right) \cdot \delta\bm{x}(t) \tag{2.3}](./f40f82c483b58386da0bfd6796a37961.png)
となります. ここで, 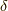 と
と 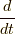 が可換であること,
が可換であること, 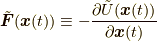 であることを用いました. こうして, 最小作用の原理, すなわち
であることを用いました. こうして, 最小作用の原理, すなわち 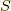 が停留点を取る(
が停留点を取る( ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}} = \bm{0}](./951af6faa2deeff8db14815fc93781b9.png) , 本節末注参照)ように軌道
, 本節末注参照)ように軌道 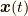 が決まるという原理から, ニュートンの運動方程式が求まります.
が決まるという原理から, ニュートンの運動方程式が求まります.

なお, (2.3)の変分で以下のオイラー・ラグランジュ方程式(Euler-Lagrange equation)を導けば,ラグランジアン密度(2.2)からニュートンの運動方程式が得られます.
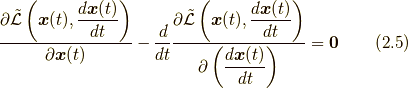
(注)ここで, ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}}](./2f628462835427b30462aaf8ae55b17c.png) は
は ![\delta S [ \bm{x} ] = \int dt m \frac{\delta S [ \bm{x} ]}{\delta \bm{x}} \cdot \delta\bm{x}(t)](./945191013d508a64b5c8b3a4f444e114.png) により定義される
により定義される 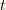 の関数です. すなわち,
の関数です. すなわち, ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}}](./2f628462835427b30462aaf8ae55b17c.png) は式(2.5)のオイラー・ラグランジュ方程式の左辺そのものです.
は式(2.5)のオイラー・ラグランジュ方程式の左辺そのものです.
3.流体力学への拡張のための道具(オイラー表現, 位置関数)
本記事では, オイラー表現(Eulerian description), すなわちすべての物理量を位置 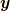 と 時間
と 時間 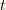 の場の量として取り扱うことにします.速度場, 密度場, 応力(の場)をそれぞれ,
の場の量として取り扱うことにします.速度場, 密度場, 応力(の場)をそれぞれ, 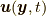 ,
, 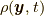 ,
, 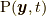 (
( 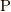 はテンソル場です.)と表すことにします.
はテンソル場です.)と表すことにします.
物理量は流体要素と共に流れていくわけですから, オイラー表現では, 物理量の時間微分はラグランジュ微分(Lagrangian derivative)(本稿ではこの名で呼ぶことにします) 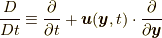 で与えられることになります.なお, 筆者は本稿でよく
で与えられることになります.なお, 筆者は本稿でよく 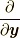 の記法を用いますが, これはより一般的記法ではナブラ
の記法を用いますが, これはより一般的記法ではナブラ  のことですので, 適宜読み替えてください.
のことですので, 適宜読み替えてください.
さて,ここで,筆者が「位置関数(position function)」と名付けた新規の場の量を導入します.それは単にその位置を返す関数です.

位置関数 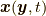 の時間微分を取ってみます.
の時間微分を取ってみます.
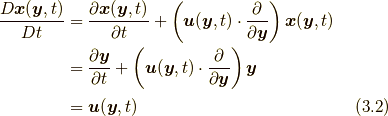
となり, この意味で位置関数は「位置」としてwell-defined(矛盾なく定まっているもの)であり, オイラー表現における「位置」の役割を果たしていることが分かります.
位置関数の変分は 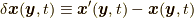 であり, 位置関数の変分
であり, 位置関数の変分 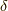 と時間微分
と時間微分 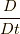 は可換になります. これで準備が整いました.
は可換になります. これで準備が整いました.
4.コーシーの運動方程式の導出
では, いよいよ流体力学の場合を考えます.戦略としては,質点の場合を「包含」するような形で作用を拡張します. それは次のような形になります.
4.1 作用
![S \left[ \bm{x} \right] &\equiv \int dt \int_{V} dV(\bm{y},t) \rho (\bm{y},t) \tilde{\mathcal{L}} \left( \bm{x}(\bm{y},t), \frac{D \bm{x}(\bm{y},t)}{Dt} \right) \\&= \int dt \int_{V} dV(\bm{y},t) \rho (\bm{y},t) \left( \frac{1}{2} \left( \frac{D \bm{x}(\bm{y},t)}{Dt} \right)^{2} +\frac{1}{\rho(\bm{y},t)}\frac{\partial \mathrm{P}(\bm{y},t)}{\partial \bm{y}} \cdot \bm{x}(\bm{y},t) - \tilde{U}(\bm{x}(\bm{y},t)) \right) \tag{4.1}](./46606e1eaba8ae026e701a003b7ab589.png)
ここで,  は, 適当な直交座標系をとって成分で書けば以下になります.
は, 適当な直交座標系をとって成分で書けば以下になります.
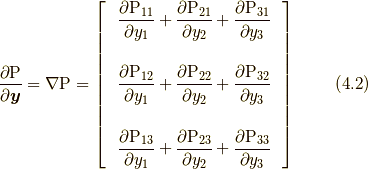
ラグランジアン密度 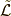 を書きだすと,
を書きだすと,
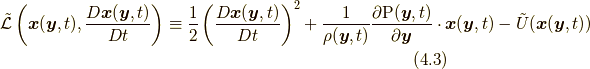
です.
なお, 式(4.2)は, 応力 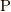 を
を ![^{t}\mathrm{P}= \left[ \bm{p}_{1} \; \bm{p}_2 \; \bm{p}_3 \right]](./676604ac0a464a9b17d85117147ea040.png) (ここで,
(ここで, 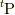 は
は 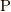 の転置行列)と列ベクトルで表わせば,
の転置行列)と列ベクトルで表わせば, 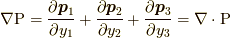 などとも表記できます.
などとも表記できます.
さて, ここで, 上記の作用(4.1)あるいはラグランジアン密度(4.3)で, 流体要素の広がり(分布)に関係する変数 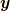 がなくなると(つまり
がなくなると(つまり 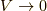 で流体要素の広がりがなくなると), 流体(連続体)の位置関数
で流体要素の広がりがなくなると), 流体(連続体)の位置関数 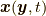 は単に質点の位置ベクトル
は単に質点の位置ベクトル 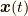 になると共に空間勾配
になると共に空間勾配 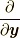 がなくなって
がなくなって 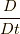 は
は 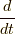 になり, 応力はそもそもないのでゼロ, あるいは全方位において作用反作用の法則で打ち消し合うものが存在し, 合計がゼロになる(
になり, 応力はそもそもないのでゼロ, あるいは全方位において作用反作用の法則で打ち消し合うものが存在し, 合計がゼロになる( 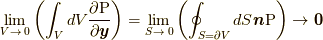 )と考えれば, 質点の場合の作用(2.1)あるいはラグランジアン密度(2.2)に対応するようになります.素朴で拙い説明ですが, この描像に大きな問題はないでしょう.ところが, もう少し繊細なそして本質的に重大な問題があります.そもそも応力
)と考えれば, 質点の場合の作用(2.1)あるいはラグランジアン密度(2.2)に対応するようになります.素朴で拙い説明ですが, この描像に大きな問題はないでしょう.ところが, もう少し繊細なそして本質的に重大な問題があります.そもそも応力 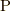 は, 変数
は, 変数 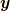 がなくなったときに, 陽に位置ベクトル
がなくなったときに, 陽に位置ベクトル 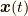 の関数であるものとして残ってはならないはずです.なぜなら, 周囲の応力が打ち消し合う以前に, ニュートンの運動方程式には存在しないものだからです.そのため, 応力
の関数であるものとして残ってはならないはずです.なぜなら, 周囲の応力が打ち消し合う以前に, ニュートンの運動方程式には存在しないものだからです.そのため, 応力 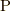 は陽に位置関数
は陽に位置関数 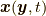 あるいはその時間微分の関数であることはできません.もしも, 応力
あるいはその時間微分の関数であることはできません.もしも, 応力 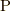 が陽に位置関数
が陽に位置関数 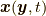 あるいはその時間微分の関数であったならば, 本稿の最小作用の原理(変分原理)の議論はすべて瓦解します.それが事実ならば仕方ありませんが, 実際には応力
あるいはその時間微分の関数であったならば, 本稿の最小作用の原理(変分原理)の議論はすべて瓦解します.それが事実ならば仕方ありませんが, 実際には応力 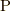 が陽に位置関数
が陽に位置関数 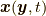 あるいはその時間微分である
あるいはその時間微分である 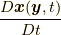 (つまり速度場
(つまり速度場 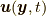 )や
)や 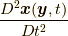 (つまり加速度場)などの関数ではないこと(このことが本稿で提案する最小作用の原理において重要な意味を持つことを強調しておきたいと思います.)を9節で明らかにしますので, ここではひとまずそれを認めて応力
(つまり加速度場)などの関数ではないこと(このことが本稿で提案する最小作用の原理において重要な意味を持つことを強調しておきたいと思います.)を9節で明らかにしますので, ここではひとまずそれを認めて応力 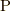 が陽に位置関数
が陽に位置関数 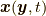 あるいはその時間微分の関数ではないという意味で応力
あるいはその時間微分の関数ではないという意味で応力 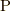 を
を 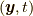 の関数として表記します(他の場の量も変数が
の関数として表記します(他の場の量も変数が 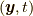 である場合には同様の意味を持ちます).
である場合には同様の意味を持ちます).
4.2 最小作用の原理
作用(4.1)について, 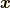 による変分を行い, 部分積分を行い, 全微分の項を境界条件により除いて整理すると,
による変分を行い, 部分積分を行い, 全微分の項を境界条件により除いて整理すると,
![\delta S \left[ \bm{x} \right] &= \int dt \left( -\int_{V} dV(\bm{y},t) \rho(\bm{y},t)\frac{D^{2}\bm{x}(\bm{y},t)}{Dt^{2}} + \int_{V} dV(\bm{y},t) \frac{\partial \mathrm{P}(\bm{y},t)}{\partial \bm{y}}+ \int_{V} dV(\bm{y},t) \rho(\bm{y},t)\tilde{F}(\bm{x}(\bm{y},t)) \right) \cdot \delta \bm{x}(\bm{y},t) \\ \\ &= \int dt \left( -\int_{V} dV(\bm{y},t) \rho(\bm{y},t)\frac{D^{2}\bm{x}(\bm{y},t)}{Dt^{2}} + \oint_{S=\partial V} dS(\bm{y},t) \bm{n}(\bm{y},t) \mathrm{P}(\bm{y},t) + \int_{V} dV(\bm{y},t) \rho(\bm{y},t)\tilde{F}(\bm{x}(\bm{y},t)) \right) \cdot \delta \bm{x}(\bm{y},t) \tag{4.4}](./963558b308a25e9a4882d8cbdbfae5c1.png)
となります. ここで, 式(4.4)の最初の等号で, 変分の結果, 応力を含む項については 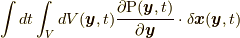 しか残っていないのは4.1節末に述べた理由によりますが, 9節において, 新しい応力の定義に基づいた補足説明をします.また, 上で部分積分を行う際に,
しか残っていないのは4.1節末に述べた理由によりますが, 9節において, 新しい応力の定義に基づいた補足説明をします.また, 上で部分積分を行う際に, ![\left[ \delta, \frac{D}{Dt} \right]=\delta \frac{D}{Dt}- \frac{D}{Dt} \delta =0](./0d3108dd8adb0195b710bd1f0643ce28.png) であることと質量保存の法則
であることと質量保存の法則 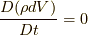 (8節を参照)を用いています.さらに, ガウスの定理
(8節を参照)を用いています.さらに, ガウスの定理 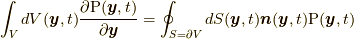 および
および 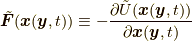 であることを用いました. こうして, 最小作用の原理, すなわち
であることを用いました. こうして, 最小作用の原理, すなわち 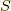 が停留点を取る(
が停留点を取る( ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}} = \bm{0}](./951af6faa2deeff8db14815fc93781b9.png) , 本節末注参照)ように「軌道」
, 本節末注参照)ように「軌道」 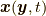 が決まるという原理から, コーシーの運動方程式が得られます.
が決まるという原理から, コーシーの運動方程式が得られます.
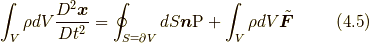
ここで, 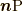 は, 適当な直交座標系をとって成分で書けば以下になります.
は, 適当な直交座標系をとって成分で書けば以下になります.
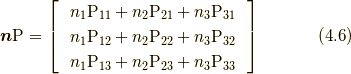
ここで, 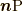 は
は 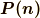 とも表し, 応力ベクトルと言います.応力ベクトルは, 応力
とも表し, 応力ベクトルと言います.応力ベクトルは, 応力 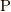 を
を ![^{t}\mathrm{P}= \left[ \bm{p}_{1} \; \bm{p}_2 \; \bm{p}_3 \right]](./676604ac0a464a9b17d85117147ea040.png) と列ベクトルで表わせば,
と列ベクトルで表わせば, 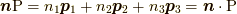 などとも表記できます.
などとも表記できます.
なお, (4.4)の変分で以下のオイラー・ラグランジュ方程式を導けば, ラグランジアン密度(4.3)からコーシーの運動方程式が得られます(式(4.7)は筆者が示したもので教科書等にはありません).
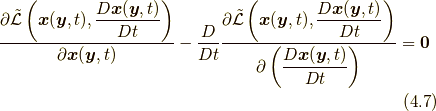
(注)ここで, ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}}](./2f628462835427b30462aaf8ae55b17c.png) は
は ![\delta S [ \bm{x} ] = \int dt \int_{V} dV(\bm{y},t) \rho (\bm{y},t) \frac{\delta S [ \bm{x} ]}{\delta \bm{x}} \cdot \delta\bm{x}(\bm{y},t)](./9e5d3f8ce88ce81ba87529426d4a502a.png) により定義される
により定義される 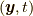 の関数です. すなわち,
の関数です. すなわち, ![\frac{\delta S [ \bm{x} ]}{\delta \bm{x}}](./2f628462835427b30462aaf8ae55b17c.png) は 式(4.7)のオイラー・ラグランジュ方程式の左辺そのものです.
は 式(4.7)のオイラー・ラグランジュ方程式の左辺そのものです.
5.最終結果には位置関数は陽には登場しなくてもよい
コーシーの運動方程式は, 式(1.2)という形以外に, 式(4.4)でガウスの定理を使う前の式から, 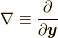 を用いると,
を用いると,
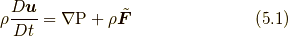
という形でも表せます. いずれにしても, 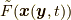 を 単に
を 単に 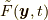 と捉えれば, 導出結果には位置関数は陽には現れなくてよいことになります. もちろん, いまや位置関数で表してもよいわけです.
と捉えれば, 導出結果には位置関数は陽には現れなくてよいことになります. もちろん, いまや位置関数で表してもよいわけです.
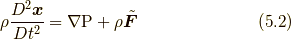
従来, 位置関数という発想が登場しなかったのは, コーシーの運動方程式から出発して議論してきており, 位置関数は陽に現れなくて済んでいたからだったのかもしれません. しかし, たとえば流体力学をハミルトン形式で記述する場合には本質的に位置関数が必要になります.
6.流体力学をハミルトン形式の力学で記述した場合
位置関数 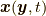 を正準変数にとり, 正準運動量
を正準変数にとり, 正準運動量 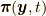 を以下で定義します.
を以下で定義します.
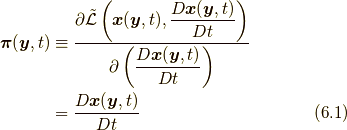
するとハミルトニアン密度は,
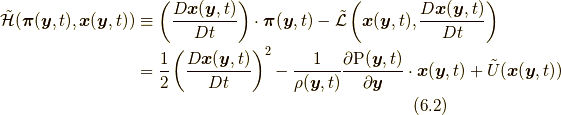
となり, 次のハミルトン方程式(Hamilton's equations)が成り立つことが容易に確認できます.
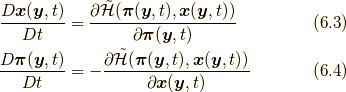
また, ハミルトン方程式により,
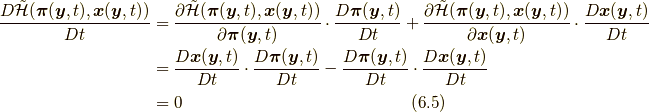
が成り立ち, 8節で説明するエネルギー保存則の別証を与えます.
7.ナヴィエ・ストークス方程式との関係 構成方程式との独立性
等方的なニュートン流体の場合, 応力は次の形になります.
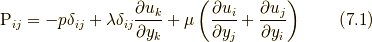
ここで, 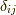 ,
, 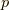 ,
, 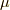 ,
, 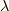 はそれぞれクロネッカーのデルタ, 圧力, 粘性率, 第2粘性率です.
はそれぞれクロネッカーのデルタ, 圧力, 粘性率, 第2粘性率です.
式(7.1)をコーシーの運動方程式(5.1)に代入すると, 以下のナヴィエ・ストークス方程式(Navier-Stokes equation)が得られます.
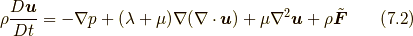
式(7.1)のように応力の具体的な形を与える式を構成方程式(Constitutive equation)と呼びますが, 上述のように, 応力は陽に位置関数やその時間微分の関数ではないため(等方的なニュートン流体の応力(7.1)も位置関数を陽には含んでいません.注意:速度勾配は含まれていますが, 位置関数の時間微分である速度場そのものは陽には含まれていません).構成方程式は一般的には, 8節で述べるように速度場の勾配(正確には変形速度テンソル)の関数になっており, そのために, 最小作用の原理によるコーシーの運動方程式の導出過程には影響せず, 最小作用の原理とは独立になっています.
8.質量保存則とエネルギー保存則
いま無重力空間に見かけ上同じ二つのボールがあったとします.一つは鉄製で一つは発泡スチロール製です.これらを同じ外力で押せば, それぞれのボールの質量に応じてニュートンの運動方程式(1.1)に従った加速度で運動をします(これは質点の話で, 厳密にはボールは弾性体や剛体でしょうから以下の連続体の枠組みに入れるべきですが).質量が連続的に広がった連続体(流体)でも事態は基本的に同じであり, ある質量場に対して外力の場が働けば各点の質量に応じた加速度で流体が運動していき, 新たに配置された質量場に対して外力の場が働けば各点の質量に応じた加速度で流体が運動していき…, ということが続いていきます.この運動がコーシーの運動方程式(1.2)に従います.
コーシーの運動方程式(1.2)では, 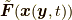 は与えられるとして, 質量場
は与えられるとして, 質量場 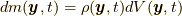 と応力場
と応力場 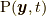 が分かっていれば, すべての位置と時間
が分かっていれば, すべての位置と時間 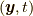 について速度場
について速度場 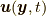 が決定され,流体の運動の状態が完全に決定されます.しかし, そのためには質量場
が決定され,流体の運動の状態が完全に決定されます.しかし, そのためには質量場 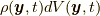 あるいは応力場
あるいは応力場 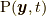 はコーシーの運動方程式とは別に決定しなければなりません.このうち質量場
はコーシーの運動方程式とは別に決定しなければなりません.このうち質量場 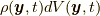 については質量保存の法則により決定できます. 質量保存則は次の形で表せます.
については質量保存の法則により決定できます. 質量保存則は次の形で表せます.
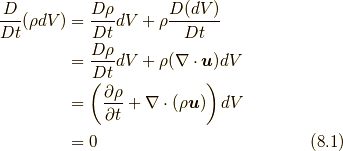
ここで, 二番目の等式で 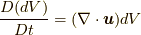 であること(
であること( 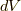 も場の量
も場の量 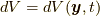 であることに注意してください), 四番目の等式で連続の式(Continuity equation)
であることに注意してください), 四番目の等式で連続の式(Continuity equation) 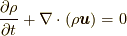 を用いています.
を用いています.
さて, 系の単位質量あたりのエネルギー(エネルギー密度) 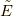 は次のようになります.
は次のようになります.
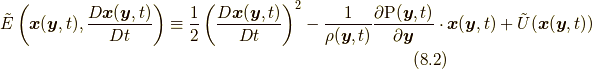
エネルギー密度 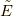 について, 以下が成り立ちます.
について, 以下が成り立ちます.
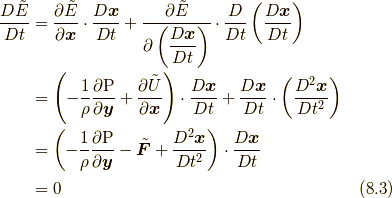
ここで, 四番目の等式でコーシーの運動方程式 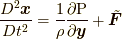 (これは式(5.2)と同じです.)を用いています.
(これは式(5.2)と同じです.)を用いています.
流体要素の系全体のエネルギー 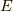 は,
は,
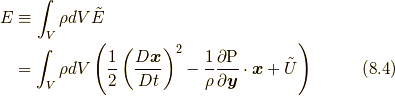
となりますが, 式(8.1)と式(8.3)から次のエネルギー保存則が示されます.
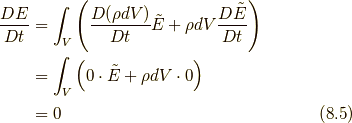
ナヴィエ・ストークス方程式(7.2)の場合には, 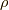 ,
, 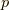 ,
, 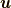 の都合5つの量がすべての
の都合5つの量がすべての 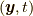 で決定されれば流体の状態が完全に決定されます.そのためには, ナヴィエ・ストークス方程式(7.2)と質量保存則(8.1)とエネルギー保存則(8.5)の式があれば十分です.
しかしより一般の流体の場合(コーシーの運動方程式(1.2)の場合)にはそれでけでは情報が不足します.たとえば非極性的な応力(non-polar stress)の流体の場合には, 応力テンソル自体には対称テンソル(
で決定されれば流体の状態が完全に決定されます.そのためには, ナヴィエ・ストークス方程式(7.2)と質量保存則(8.1)とエネルギー保存則(8.5)の式があれば十分です.
しかしより一般の流体の場合(コーシーの運動方程式(1.2)の場合)にはそれでけでは情報が不足します.たとえば非極性的な応力(non-polar stress)の流体の場合には, 応力テンソル自体には対称テンソル( 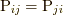 )であるといった性質しかないため, その6個の独立成分を決定する方程式系が必要になります.当然のことながら, 構成方程式(7.1)は前提できません.
)であるといった性質しかないため, その6個の独立成分を決定する方程式系が必要になります.当然のことながら, 構成方程式(7.1)は前提できません.
伝統的な流体力学では, 応力を決定するにあたっては, 通常はもっとも一般的な形として, 応力テンソル 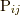 には剛体回転
には剛体回転 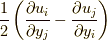 は寄与しないとして, 変形速度テンソル(あるいはひずみテンソル)
は寄与しないとして, 変形速度テンソル(あるいはひずみテンソル) 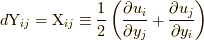 の関数と考え(つまり
の関数と考え(つまり 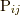 を非極性的な応力で対称テンソルととらえ), 以下の式(8.6)から応力テンソル
を非極性的な応力で対称テンソルととらえ), 以下の式(8.6)から応力テンソル 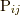 の関数形を決定しています.
の関数形を決定しています.
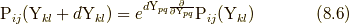
ただし, ここで 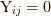 であり,
であり, 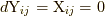 のとき,
のとき, 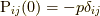 (
( 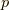 は圧力で, 弾性体ではゼロ)です.ナヴィエ・ストークス方程式の構成方程式(7.1)は, 式(8.6)の右辺で一次の微分項まで考えたものに対応しています.
は圧力で, 弾性体ではゼロ)です.ナヴィエ・ストークス方程式の構成方程式(7.1)は, 式(8.6)の右辺で一次の微分項まで考えたものに対応しています.
応力の関数形の決定にあたっては, その条件として質量保存則(8.1)やエネルギー保存則(8.5)を用いることができます.また, もしナヴィエ・ストークス方程式の場合のような構成方程式が別に得られているのならばそれを用いることができます.
しかし応力をもっとずばり示してくれる式はないのでしょうか?  そもそも一体, 応力とは何なのでしょうか?
そもそも一体, 応力とは何なのでしょうか?  次節ではそのことをもう一度考え直し, 新しい形での応力を提示します.そして応力が位置関数あるいはその時間微分を陽に含んでいないということも確認します.
次節ではそのことをもう一度考え直し, 新しい形での応力を提示します.そして応力が位置関数あるいはその時間微分を陽に含んでいないということも確認します.
9.応力の新しい形の提示
本記事では, 連続体に関するコーシーの運動方程式を, 質点に関するニュートンの運動方程式を拡張したものとして捉えていますが, そのような観点で見た場合に, 応力とは何なのでしょうか?  本稿では物理量はすべて場の量として扱っていますが, 質点の場合と本質的には変わらず連続体の運動の状態も, すべての位置
本稿では物理量はすべて場の量として扱っていますが, 質点の場合と本質的には変わらず連続体の運動の状態も, すべての位置 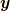 と時刻
と時刻 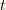 での質量場
での質量場 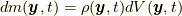 と速度場
と速度場 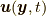 を決定できれば決定します.8節冒頭の説明からそれが分かりますが, そこに応力は登場しません.登場する必要はないのです.なぜなら, 応力とは, 近接した位置での質量場と速度場の関係の名に過ぎないからです.実際, 応力は以下に示すように質量場と速度場だけを使ってexplicitに表せます.
を決定できれば決定します.8節冒頭の説明からそれが分かりますが, そこに応力は登場しません.登場する必要はないのです.なぜなら, 応力とは, 近接した位置での質量場と速度場の関係の名に過ぎないからです.実際, 応力は以下に示すように質量場と速度場だけを使ってexplicitに表せます.
流れの場があったときに, 質量場と速度場でできる運動量(的な量) 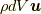 , の時間微分による力(的な量)
, の時間微分による力(的な量) 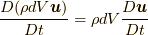 , の近接した位置
, の近接した位置 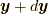 と
と 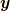 での差
での差 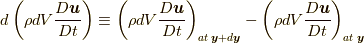 , から応力を定義できます.すなわち,
, から応力を定義できます.すなわち,
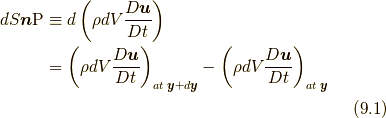
位置の変位 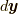 による変位(つまりはテイラー展開)を明示すれば,
による変位(つまりはテイラー展開)を明示すれば,
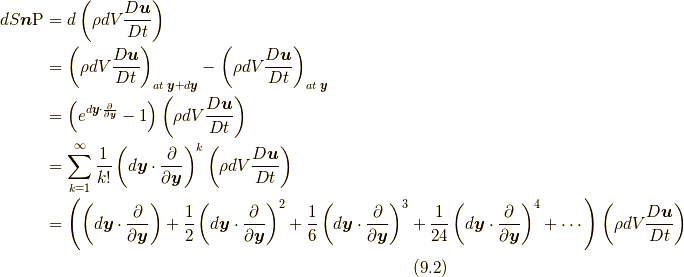
となります.ここで, 面積要素ベクトル 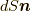 と変位ベクトル
と変位ベクトル 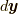 は平行です(つまり
は平行です(つまり 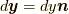 と書けます).また, ここでは著者独自の指数関数を用いた表記でテイラー展開を
と書けます).また, ここでは著者独自の指数関数を用いた表記でテイラー展開を 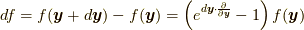 と表現しています.ここではもっとも一般的な連続体を想定するため, 近似は行わずあえて高次の項を残しています(無限級数にしておかないと, 連続体の方程式としてはおそらく完結しません).式(9.1)を応力ベクトル
と表現しています.ここではもっとも一般的な連続体を想定するため, 近似は行わずあえて高次の項を残しています(無限級数にしておかないと, 連続体の方程式としてはおそらく完結しません).式(9.1)を応力ベクトル 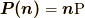 の定義としてみなせば,
の定義としてみなせば,
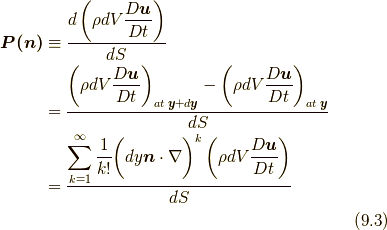
となります.流体要素との絡みで応力を見る場合には, 流体要素の表面上の任意の点 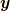 について,
について, 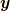 に近接した外側の点
に近接した外側の点 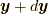 と
と 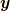 との間での力的な量
との間での力的な量 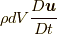 の差から定義することになります(以下の図を参照してください).
の差から定義することになります(以下の図を参照してください).
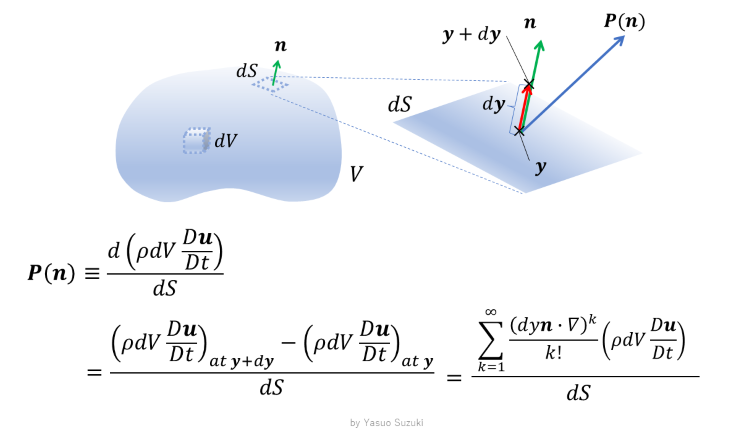
式(9.1)や(9.2)は適当な直交座標系の成分で書けば, 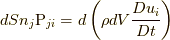 や
や 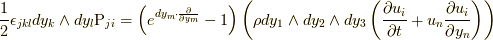 ( ここで,
( ここで, 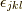 はレビ・チビタ記号,
はレビ・チビタ記号, 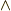 はウェッジ積です )などと表せます.このような成分による表記を用いれば, 応力の定義式(9.1),(9.2)あるいは(9.3)により,
はウェッジ積です )などと表せます.このような成分による表記を用いれば, 応力の定義式(9.1),(9.2)あるいは(9.3)により,
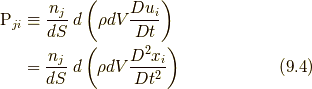
と表せることが分かります.
(ここで, もし気になった方がいた時のために少し立ち入った注意をしますと, 式(9.2)の位置の変位 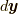 による変位(テイラー展開)を考えるにあたっては, ある時刻(時点)を固定してその時刻(時点)における空間的な変位分だけを考えれば充分です. ですから, 位置の変位
による変位(テイラー展開)を考えるにあたっては, ある時刻(時点)を固定してその時刻(時点)における空間的な変位分だけを考えれば充分です. ですから, 位置の変位 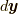 の時間に対する変位分
の時間に対する変位分 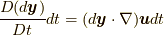 は関与しません.そのため, 微分演算子も空間勾配
は関与しません.そのため, 微分演算子も空間勾配 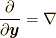 のみになっています.たとえば,
のみになっています.たとえば, 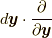 に対して,
に対して, 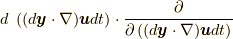 等を考える必要はありません.また, これに対応して, 式(9.2)左辺の
等を考える必要はありません.また, これに対応して, 式(9.2)左辺の 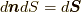 についても同様に,
についても同様に, 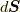 の時間に対する変位分
の時間に対する変位分 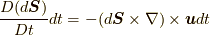 も関与しません.これらの量は
も関与しません.これらの量は 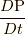 を計算する際に関与します.なお,
を計算する際に関与します.なお, 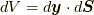 であることから,
であることから, 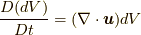 となっています.)
となっています.)
式(9.1)から(9.4)で与える応力の定義は, 応力テンソルを対称テンソルに限定しません.つまり, 非極性的な応力の流体のみならず,一般の流体, 一般の連続体の応力の定義を与えるものになっています. また, 本定義で定義される応力はあきらかに速度勾配テンソル(つまりは変形速度テンソル)の関数であるため, 従来の応力と整合するものとなっています.たとえば流体が等方的なニュートン流体の条件を満たすならば, 教科書にある通りの議論でナヴィエ・ストークス方程式の応力が得られ, 本稿で提示する応力による流体力学の定式化がナヴィエ・ストークス方程式も包含していることが分かります.
本定義は, 応力の事態の定性的な把握がしやすく, たとえば式(9.1)から, 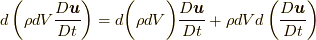 であるので, 流体が一瞬で凍結すれば質量場と速度場の勾配は共にゼロであることから, 応力はゼロになることなども分かります.
であるので, 流体が一瞬で凍結すれば質量場と速度場の勾配は共にゼロであることから, 応力はゼロになることなども分かります.
また, 筆者がここに初めて示す応力の定義式(9.1)から(9.4)は, 4.1節末に述べた, 応力が位置関数あるいはその時間微分を陽に含まないという素朴な前提を直接証明するものになっています.このことを踏まえ, 4.2節で予告した補足説明をします.問題となるのは, 式(4.1)の変分での,
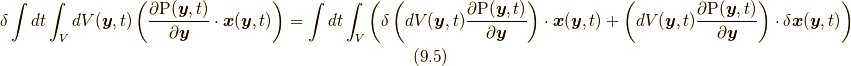
における右辺第一項ですが, 上記応力の定義式(9.1)から(9.4)により, あきらかに応力 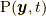 は, 陽に
は, 陽に 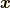 の関数でも,
の関数でも, 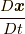 の関数でもありません.では,
の関数でもありません.では, 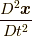 やそれ以上の階数の位置関数の時間微分についてはどうでしょうか.それらの関数でもありません.なぜなら, 応力
やそれ以上の階数の位置関数の時間微分についてはどうでしょうか.それらの関数でもありません.なぜなら, 応力 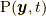 は, 近接した位置での「力的な量」の「差」
は, 近接した位置での「力的な量」の「差」 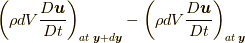 の関数ではあっても, (陽に)加速度場の関数であるわけではないからです.このことから,
の関数ではあっても, (陽に)加速度場の関数であるわけではないからです.このことから, 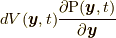 も陽に
も陽に 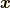 やその時間微分の関数ではないため,
やその時間微分の関数ではないため, 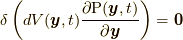 と結論づけられます.したがって, 式(9.5)の右辺第一項はゼロになります.以上で補足説明は終わりです.
と結論づけられます.したがって, 式(9.5)の右辺第一項はゼロになります.以上で補足説明は終わりです.
さて, そもそも応力というものは, ものの流れを先に立てて考えれば, その結果的な力であり, またある意味では見かけ上の力であるに過ぎないのです.ですから, 式(9.1), (9.2)あるいは(9.3)を使えば, 流体の基礎方程式であるコーシーの運動方程式(1.2)は,
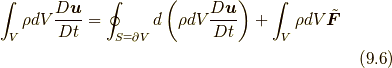
あるいは
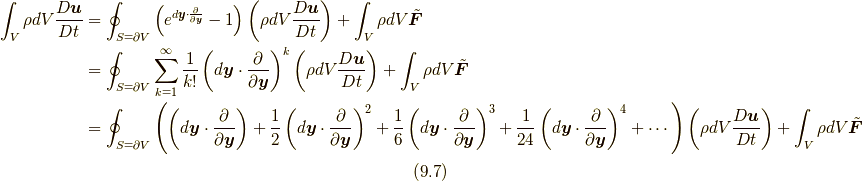
という形で表すことができ, ここにはもう応力は要りません.もし原因力と結果力という言い方をするならば, 外力の場 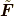 という原因力によって質量場
という原因力によって質量場 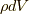 と速度場
と速度場 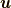 が決定されるので, それらの結果的な力(的な量)としてあえて応力というものを定義することもできる, というだけです.なお, 式(9.6)は, 形式的に,
が決定されるので, それらの結果的な力(的な量)としてあえて応力というものを定義することもできる, というだけです.なお, 式(9.6)は, 形式的に,
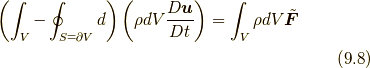
と書け, 式(9.8)は, 流体要素の各部にかかる外力の合計(式(9.8)右辺)を,流体要素内部上の積分演算子と流体要素表面からの微分についての流体要素表面上の積分演算子との差を受ける形で流体の「力的な量」を展開して流体の運動状態を決めている式になっているとみなすことができます. 今仮に, 宇宙全体が一つの古典的な流体であったとすると, その外側には外力はない(式(9.8)右辺はゼロである)ので, 宇宙(流体要素内部)上の積分演算子が宇宙の境界(流体要素表面)からの微分についての宇宙の境界(流体要素表面)上の積分という演算子と等価であるように宇宙が運動することになります.
ところで, 式(9.6)あるいは(9.7)では, 粘性はどこへ消えてしまったのかと思う方がいるかもしれません.心配いりません.粘性とはもとをたどれば慣性に起因しているので, 質量場 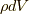 のところに含まれているのです.
のところに含まれているのです.
流体(より一般的には連続体)で決定すべきは質量場 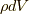 と速度場
と速度場 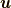 だけであるので, 実は質量保存則の式(8.1)とコーシーの運動方程式(9.6)あるいは(9.7)だけがあれば決定されてしまいます.そのため, 流体力学の基礎方程式を改めて記すならば, 次の式にまとめられます(興味のある方は相対論的にこれをさらに一つの式にまとめていただければと思います!
だけであるので, 実は質量保存則の式(8.1)とコーシーの運動方程式(9.6)あるいは(9.7)だけがあれば決定されてしまいます.そのため, 流体力学の基礎方程式を改めて記すならば, 次の式にまとめられます(興味のある方は相対論的にこれをさらに一つの式にまとめていただければと思います!  ).
).
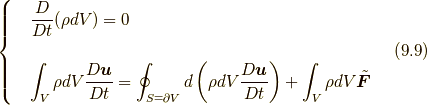
あるいは
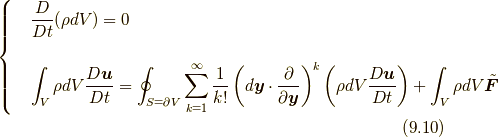
ここに流体の運動の状態を決定するのに必要十分な情報があることに注目してください.このような定式化は従来存在しなかったものです.ナヴィエ・ストークス方程式などでは, ある意味では余計なパラメータを導入して応力を近似しているため,流体の状態の決定に必要な方程式が余計に増えてしまっていたのです.
最後に, 本記事で質点に関するニュートンの運動方程式を包含する目的で導入した位置関数との関連について述べます.ここでは「位置場(position field)」と呼んだ方が適切かもしれませんので位置場と呼ぶことにします(考えてみれば, 加速度場も速度場もあるので位置場というものもあってよいでしょう!  ). 位置場
). 位置場 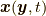 を用いると, 式(9.10)は以下の式(9.11)になりますが, 式(9.11)により, 連続体はすべての位置と時刻
を用いると, 式(9.10)は以下の式(9.11)になりますが, 式(9.11)により, 連続体はすべての位置と時刻 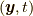 での質量場
での質量場 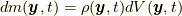 と位置場
と位置場 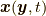 を決定すれば決定されると表現でき, また, 連続体力学を, 質点の運動を包含しつつそれを拡張させた形で定式化することが可能になります.
を決定すれば決定されると表現でき, また, 連続体力学を, 質点の運動を包含しつつそれを拡張させた形で定式化することが可能になります.
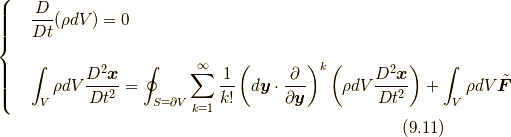
しかしながら, 式(9.11)の解である位置場 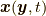 はその定義式(3.1)より自明であり, その意味で式(9.11)の
はその定義式(3.1)より自明であり, その意味で式(9.11)の 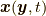 についてはもう解けてしまっており, しかも不思議なことにその解は質量場や外力の場に全然依っていません! この不思議の秘密はラグランジュ微分にあります.ラグランジュ微分には速度場が含まれ, そこに質量場や外力の場の影響が吸収されているわけです.速度場は位置場のラグランジュ微分から求められますが, そこにまた速度場が含まれ…という本節の終わりに述べる, 位置場を導入すると見える速度場のある性質(速度場の内的開展)により, 流体の状態を知るには実質的にはやはり式(9.10)を解くことになり, したがって質量場や外力の場を考慮することになり, 式(9.10)の
についてはもう解けてしまっており, しかも不思議なことにその解は質量場や外力の場に全然依っていません! この不思議の秘密はラグランジュ微分にあります.ラグランジュ微分には速度場が含まれ, そこに質量場や外力の場の影響が吸収されているわけです.速度場は位置場のラグランジュ微分から求められますが, そこにまた速度場が含まれ…という本節の終わりに述べる, 位置場を導入すると見える速度場のある性質(速度場の内的開展)により, 流体の状態を知るには実質的にはやはり式(9.10)を解くことになり, したがって質量場や外力の場を考慮することになり, 式(9.10)の 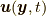 のように解が自明ではなくなります.
以上のような事情もまた, 位置場が歴史上登場しなかったimplicitな理由であったのかもしれません.
のように解が自明ではなくなります.
以上のような事情もまた, 位置場が歴史上登場しなかったimplicitな理由であったのかもしれません.
なお, 主題が拡散し過ぎてしまうのでここでは立ち入りませんが, 式(9.10)あるいは(9.11)は, 当然のことではありますが, 質点系の運動方程式において, 質点系の中にある閉じた境界を設定し, その領域についての運動を記述する式を考えた場合と整合しています.
最後に, 位置場を導入することにより見える速度場のある性質について説明します.速度場は, 位置場のラグランジュ微分で表されますが, そのラグランジュ微分の中にまた速度場がありますので, それもまた位置場のラグランジュ微分で表され, そのラグランジュ微分の中にまた速度場があるのでそれもまた位置場のラグランジュ微分で表され…と, 無限に開展する構造があります.筆者はこの性質を速度場の内的開展と呼んでいますが, これは連続体というものの特性を表していると考えられます.
10.おわりに
ここに提案した議論の特長は, (i)従来の質点に関するニュートンの運動方程式を導く最小作用の原理あるいは変分原理を, 位置関数というものを導入する事によって, 連続体の運動方程式に拡張できたこと, (ii)この定式化により, 熱力学を援用しない形で連続体力学を完結できたこと, (iii)応力が何であるかをその新しい形を明示的に提示することによって示し, 粘性の意味も含めて, 連続体力学の基礎を直截に定式化できたことにあるのではないかと思います.
以下は物理学とは関係のない経緯的余談です.
本記事の内容(問題)は, 15歳のころから素粒子物理学を志したものの哲学的な問題に関心があったことに気づき, 1993年(23歳)に物理をやめてしまった筆者鈴木康夫が, 2000年になって当時の仕事の中でたまたまさる高名な流体物理学の先生から「流体力学の変分原理はまだない」と教わり, 流体力学のことは全く知らなかったのになぜか興味を持ち, 木田重雄先生の教科書でコーシーの運動方程式を眺めているうちにニュートンの運動方程式の変分原理の拡張として理論が構築できるのではないかと考え, 以来, 二十数年間(年月は重要ではありませんが, 気づけば自分がどこにいるか分からなくなってしまう怖いものがあります), つらつらと独りで勝手に考察してきた意味でオリジナルな理論であり, 世の中に広まっているものではありません.二十数年とは言っても, 直線的な道のりではなく, 当初持ってしまった誤謬( 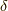 と
と 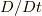 の非可換性という思い込み)に引きずられてしまい, それに気づくまで十六年以上失敗し続けました.途中, 先の先生をはじめ数人の天才たちの励ましがあり, 自らはっきりと誤謬に気づけた2016年9月17日, かつて説明の方便として導入していた位置関数なるものを使って最初からすべてを組み立て直したところ, 本稿1節から7節までの内容が1時間程度でまとまったのですが, できあがったものが意外なほど簡単な形をしていたため, 完全に拍子抜けしました.筆者はもう学術的なコミュニティに属していなったこともあって発表の場はありませんでした.論文発表を試みたものの, ある教授からは過去の研究成果のsurveyとどこをimproveしたのかが書いていないからだめ, ある学会からは実験的検証がないからだめ, あるいは研究機関に属していないからだめ, とけんもほろろに発表の申し出を断られ, そのまま一年半あまりが過ぎました.その間, ある哲学者やある友人の知り合いの物理学者の応援があり, 再度発表の場を探していたら, 物理のかぎしっぽに出会いました.物理のかぎしっぽのクロメルさんだけが即座に本理論提案の重要性を認め, 査読申請を許可してくださいました.そのお蔭で本稿が日の目を見ることとなりました.2018年2月18日に記事にして以来, 応力が陽に位置関数あるいはその時間微分の関数ではないことの理解は正しい(というかそうでなければならない)と知っていましたが, その説明があまりにナイーブ過ぎると気になっていました.その論証を考える過程で, 流体のエネルギーの保存則について位置関数を用いれば従来より違和感を感じていた熱力学の援用をしない形での証明ができるのではないかと2020年3月27日に気づいて副産物的に8節が追加されました.肝心の問題については, 応力のexplicitな定義を示すことにより解消(応力が陽に位置関数あるいはその時間微分の関数ではないことを明確に証明)できるのではないかと考えて検討を続けましたが, 2019年10月以降, 不測の人生上最大の危機に見舞われ, それまでの探究生活の土台が粉々に破壊されてしまい, 考えることすらままならない状態になってしまいました.それでもしつこく続けてはいたのですが, とうとう思考力と体力の限界を感じきっぱりあきらめてしまった経緯がありました(2020年5月17日).しかし, 2020年11月14日のある不思議な出来事(書店で哲学者永井均先生の本を立ち読みしていた際, ある少女が出現し, 理工書コーナーへいざなう彼女についていくと, いきなり力学の本を取り出し「力積」の項を指し示されました)がきっかけとなり, 2020年11月20日に新しい応力の定義(式(9.1)から(9.4))に考え至りました.8節までは既存の枠組みの再構成に過ぎない作業でしたが, 応力の新定義に基づいた9節を書くにあたっては, 比較参照すべきいかなるreferencesも存在しなかったために, なけなしの洞察力で這いずるしかない, 前人未到の, 孤独の極みの, 正気と狂気の狭間の領域に踏み込んでしまった感がありました.
本記事の内容については, 折に触れ徹底的に自己批判的な検討を重ね, 議論全体が崩壊しそうな疑念が何度も生じ(そんな時は, 学生の時分にある先生に数式の導出を説明していた際のミスに対して「私の前では決してでたらめを言うな!」と怒鳴られた時の萎縮がよみがえりました), その壊滅的自問に死にそうな苦闘を強いられましたが, めげずに論証を進めた結果, 議論が深化こそすれ, 修正すべき点はついに見つかりませんでした.
の非可換性という思い込み)に引きずられてしまい, それに気づくまで十六年以上失敗し続けました.途中, 先の先生をはじめ数人の天才たちの励ましがあり, 自らはっきりと誤謬に気づけた2016年9月17日, かつて説明の方便として導入していた位置関数なるものを使って最初からすべてを組み立て直したところ, 本稿1節から7節までの内容が1時間程度でまとまったのですが, できあがったものが意外なほど簡単な形をしていたため, 完全に拍子抜けしました.筆者はもう学術的なコミュニティに属していなったこともあって発表の場はありませんでした.論文発表を試みたものの, ある教授からは過去の研究成果のsurveyとどこをimproveしたのかが書いていないからだめ, ある学会からは実験的検証がないからだめ, あるいは研究機関に属していないからだめ, とけんもほろろに発表の申し出を断られ, そのまま一年半あまりが過ぎました.その間, ある哲学者やある友人の知り合いの物理学者の応援があり, 再度発表の場を探していたら, 物理のかぎしっぽに出会いました.物理のかぎしっぽのクロメルさんだけが即座に本理論提案の重要性を認め, 査読申請を許可してくださいました.そのお蔭で本稿が日の目を見ることとなりました.2018年2月18日に記事にして以来, 応力が陽に位置関数あるいはその時間微分の関数ではないことの理解は正しい(というかそうでなければならない)と知っていましたが, その説明があまりにナイーブ過ぎると気になっていました.その論証を考える過程で, 流体のエネルギーの保存則について位置関数を用いれば従来より違和感を感じていた熱力学の援用をしない形での証明ができるのではないかと2020年3月27日に気づいて副産物的に8節が追加されました.肝心の問題については, 応力のexplicitな定義を示すことにより解消(応力が陽に位置関数あるいはその時間微分の関数ではないことを明確に証明)できるのではないかと考えて検討を続けましたが, 2019年10月以降, 不測の人生上最大の危機に見舞われ, それまでの探究生活の土台が粉々に破壊されてしまい, 考えることすらままならない状態になってしまいました.それでもしつこく続けてはいたのですが, とうとう思考力と体力の限界を感じきっぱりあきらめてしまった経緯がありました(2020年5月17日).しかし, 2020年11月14日のある不思議な出来事(書店で哲学者永井均先生の本を立ち読みしていた際, ある少女が出現し, 理工書コーナーへいざなう彼女についていくと, いきなり力学の本を取り出し「力積」の項を指し示されました)がきっかけとなり, 2020年11月20日に新しい応力の定義(式(9.1)から(9.4))に考え至りました.8節までは既存の枠組みの再構成に過ぎない作業でしたが, 応力の新定義に基づいた9節を書くにあたっては, 比較参照すべきいかなるreferencesも存在しなかったために, なけなしの洞察力で這いずるしかない, 前人未到の, 孤独の極みの, 正気と狂気の狭間の領域に踏み込んでしまった感がありました.
本記事の内容については, 折に触れ徹底的に自己批判的な検討を重ね, 議論全体が崩壊しそうな疑念が何度も生じ(そんな時は, 学生の時分にある先生に数式の導出を説明していた際のミスに対して「私の前では決してでたらめを言うな!」と怒鳴られた時の萎縮がよみがえりました), その壊滅的自問に死にそうな苦闘を強いられましたが, めげずに論証を進めた結果, 議論が深化こそすれ, 修正すべき点はついに見つかりませんでした.
私の理論を見せたある友人からは, 「君は独りだけまったく別の世界で流体力学を考えているようだね」と(おそらく悪い意味で)評されましたが(何事につけ, 私にはどうもそういう傾向があるようです), その通りであり, 本記事に示した理論が物理学にとって意味があるのかは不明です.もちろんまったく間違っている可能性も否定できません. ただ, 少なくとも筆者にとっては, 本理論によって質点の力学と連続体の力学とが形式的に統合され, 古典力学の文脈においてはどうも隔靴掻痒の感のあった従来の定式化に関し, 満足のいく「言葉づかい」が得られた意味で重要でした.ただし, この定式化が実際上役に立つかどうかはまた別問題と理解しています.
ここから先は, 読者諸賢がこの拙い提案を批判的に吟味され, よりよい理論の構築に向けて, 間違いであればこれを棄却し, 正しいところがあるならばこれを発展いただき, 自分自身の物理学を創始されることを願っています. 筆者自身は, 本稿理論の計算機などによる検証が可能なのか知りたいところです.また, 本稿理論の相対論化や量子論化に興味はあるものの, 筆者自身にはもはや余力がなく, どなたかが構築された暁にはぜひ学ばせていただきたいです.
なお, もし, 流体力学の変分原理の問題に真剣に取り組まれたい方がおられた場合には, すでに深川宏樹先生が2012年の論文で厳密な定式化と共に問題を根本的に解決されておられますので, 所詮は素人の鈴木康夫が自分のこだわりで駄弁を弄している本稿などではなく, 何よりもまずはそちらをご精読いただくようお願いいたします.
最後に, 断片的なものではありますが, 以下, 本稿に関連する筆者のメモを紹介したいと思います.
本稿の1節から7節の変分原理の部分についてやや詳しい計算を記した英文メモ(An English Memo: Principle of Least Action in Fluid Mechanics)が こちら にあります.
本稿とは定式化の順序を応力の定義から変分原理へと逆に構成した(本稿の議論が正しいならば, むしろそのように構成し直すべきかもしれません), ある場所でのプレゼン資料が こちら2 にあります.同様の内容が下記書籍試し読み内で文章にて確認できます.
本稿の応力の定義の妥当性を考察していた際のメモを こちら3 に載せました.また,本稿検討のごく初期のころに接線応力ベクトルについて持っていた疑問についてのメモがあったので同様のことにつまずいている方のためにメモを こちら4 に載せました.
本稿は, 2021年8月27日に『鈴木康夫 流体力学』(万象企画)として一度書籍化されておりますが, 証明の面においては, 本稿の改訂の方が新しく, 一歩進んでいます.余談(特に少女の件)については書籍の方が少しだけ詳しいです.
こちら5 に本稿の英訳(An English translation of this article)が, さらに, プレゼン動画(An English presentation movie)が こちら6 にあります.
式(4.7)の証明のメモが こちら7 にあります.
最後に, もし鈴木康夫に連絡を取りたい方がおられた場合には, physicish at gmail.comまでお願いいたします.