等速運動する荷電粒子の磁場のエネルギー
真空中で電荷 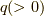 ,質量
,質量  を持つ荷電粒子が,
ある慣性系Σに対して,z軸方向に一定速度
を持つ荷電粒子が,
ある慣性系Σに対して,z軸方向に一定速度 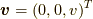 で運動する時を
考えます.
で運動する時を
考えます.  は転置を表すことにします.
その電荷が作る磁場のエネルギーを知りたいのです.
は転置を表すことにします.
その電荷が作る磁場のエネルギーを知りたいのです.
点電荷では発散してしまう
その荷電粒子を原点に持つ別の慣性系をΣ’で表し,
Σ’の物理量をダッシュ(’)をつけて区別することにします.
Σ’系はΣ系に対し,速度 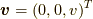 で動いているわけです.
今,二つの慣性系が時刻
で動いているわけです.
今,二つの慣性系が時刻 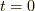 で一致する時を考えます.
Σ’系から見た電束密度を
で一致する時を考えます.
Σ’系から見た電束密度を 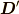 とします.
ビオ・サバールの法則によると,作られる磁場
とします.
ビオ・サバールの法則によると,作られる磁場 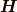 は,
は,

となります [*] .Σ’系の動径方向単位ベクトルを 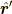 とすると,
Σ’系での荷電粒子は静止しているので,それが作る電束密度
とすると,
Σ’系での荷電粒子は静止しているので,それが作る電束密度 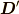 は,
電場
は,
電場 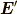 に真空の誘電率
に真空の誘電率 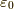 を掛けたものなので,
を掛けたものなので,
| [*] | ちなみに,この表式は特殊相対論での非相対論的極限と一致します. |

となります.二つ目の等号は時刻 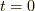 で原点が一致しているので,
動径ベクトルが一致している為です.よって,式
で原点が一致しているので,
動径ベクトルが一致している為です.よって,式 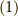 にこれを代入して,
真空の透磁率
にこれを代入して,
真空の透磁率 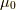 を掛けて,磁束密度の表式にすると,
を掛けて,磁束密度の表式にすると,
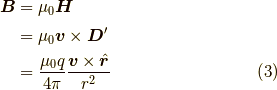
ちなみにこの式を,向き 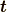 を持つ電流要素
を持つ電流要素 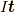 が存在する時の,
ビオ・サバールの法則と比較すると,
が存在する時の,
ビオ・サバールの法則と比較すると,
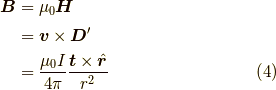
ですから,

であることが分かります.ここで, 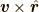 を計算すると,
を計算すると,
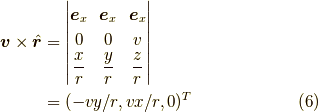
となります.
式 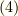 より,この磁場が作る磁場のエネルギー
より,この磁場が作る磁場のエネルギー 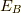 を求めると,極座標
を求めると,極座標 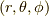 を導入して,
粒子の大きさがない点として考えると,
を導入して,
粒子の大きさがない点として考えると,
![E_B &= \int \bm{B} \cdot \bm{H} dV \\&= \dfrac{1}{\mu_0} \int \bm{B}^2 dV \\&= \dfrac{1}{\mu_0}\dfrac{\mu_0^2}{16 \pi^2} \int \dfrac{q^2 }{r^4} (\bm{v} \cdot \hat{\bm{r}})^2 dV \\&= \dfrac{\mu_0}{16 \pi^2} \int \dfrac{q^2 }{r^4} \left( (vy/r)^2+(vx/r)^2 \right) dV \\&= \dfrac{\mu_0}{16 \pi^2} \int \dfrac{q^2 v^2}{r^4} \left( (\sin \theta \sin \phi)^2+(\sin \theta \cos \phi)^2 \right) dV \\ &= \dfrac{\mu_0}{16 \pi^2} \int \dfrac{q^2 v^2}{r^2} \left( (\sin \theta)^3 \right) dr d\theta d\phi \\&= \dfrac{\mu_0 q^2 v^2}{16 \pi^2} \left[ -\dfrac{1}{r} \right]_0^\infty \left[ \dfrac{\cos \theta}{3} - \cos \theta \right]_0^\pi \left[ \phi \right]_0^{2\pi} \\&\to \infty \tag{7}](./bbc6d8ccb7a0ba1e81e7e771df779631.png)
となり,r方向の積分が,原点付近のエネルギーにより発散してしまいます.
電荷分布は発散しない
と,ここで地球の作る重力場はなぜ発散しないか思い出してみましょう.
私の以前の記事 球殻のつくる重力ポテンシャル を見ると,
質量が点ではなく,一様に分布することで発散を防いでいることが分かります.
では,電荷が半径  の球内に一様に電荷
の球内に一様に電荷 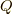 が分布していると考えてみましょう.
ガウスの法則より,電束密度は,
が分布していると考えてみましょう.
ガウスの法則より,電束密度は,
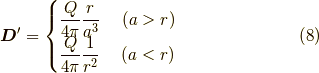
スカラーポテンシャル 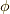 は,
は,
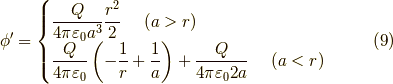
となります.ここでポテンシャルの観測点  と電荷分布のある点
と電荷分布のある点 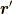 として,
スカラーポテンシャル
として,
スカラーポテンシャル 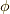 の表式(電場)と,ベクトルポテンシャル
の表式(電場)と,ベクトルポテンシャル 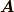 の表式(磁場)を比較してみましょう.
それは,電荷分布
の表式(磁場)を比較してみましょう.
それは,電荷分布 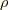 を積分
を積分 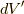 することによって,
することによって,
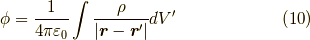
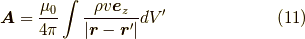
となります.ベクトル 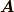 のz成分のみに注目すれば,少し係数を変えれば,
全く同じ計算であることが分かります.
のz成分のみに注目すれば,少し係数を変えれば,
全く同じ計算であることが分かります.
よって,z方向へ速さ  で動く荷電粒子の作る磁場のベクトルポテンシャル
で動く荷電粒子の作る磁場のベクトルポテンシャル 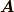 は,
は,
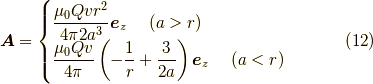
となります.磁場は 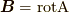 より,
より,
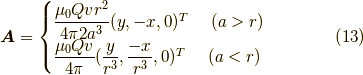
半径  の球外のエネルギー
の球外のエネルギー 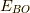 は,式
は,式 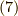 とrの積分範囲が違うだけで,同じ計算であり,
とrの積分範囲が違うだけで,同じ計算であり,
![E_{BO} &= \dfrac{1}{\mu_0} \int \bm{B}^2 dV \\&= \dfrac{\mu_0}{16 \pi^2} \int \dfrac{Q^2 v^2}{r^2} \left( (\sin \theta)^3 \right) dr d\theta d\phi \\&= \dfrac{\mu_0 Q^2 v^2}{16 \pi^2} \left[ -\dfrac{1}{r} \right]_a^\infty \left[ \dfrac{\cos \theta}{3} - \cos \theta \right]_0^\pi \left[ \phi \right]_0^{2\pi} \\&= \dfrac{\mu_0 Q^2 v^2}{4 \pi} \dfrac{2}{3a} \tag{14}](./b0c8a573b01b5201dba99fa635c4aa28.png)
です.そして,球内では,
![E_{BI} &= \dfrac{1}{\mu_0} \int \bm{B}^2 dV \\&= \dfrac{\mu_0 Q^2 v^2}{16 \pi^2 a^6} \int \left( y^2+x^2 \right) r^2 \sin \theta dr d\theta d\phi \\&= \dfrac{\mu_0 Q^2 v^2}{16 \pi^2 a^6} \int r^4 \sin^3 \theta dr d\theta d\phi \\&= \dfrac{\mu_0 Q^2 v^2}{16 \pi^2 a^6} [\dfrac{r^5}{5}]_0^a [\dfrac{\cos^3\theta}{3}-\cos \theta]_0^\pi [\phi]_0^{2\pi} \\&= \dfrac{\mu_0 Q^2 v^2}{4 \pi} \dfrac{2}{15a} \tag{15}](./aee441c15892212f7230285445e4d699.png)
よって,磁場の総エネルギーは,
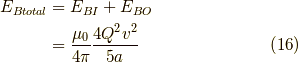
となります. あもんノート のあもんさんによると,このように電磁気エネルギーの発散を防ぐには, 電磁気それだけではダメで,電荷分布をつなぎとめておく別種の力が必要なのだそうです. 勉強になりました.
お疲れ様でした.それでは,今日はこの辺で.