尖端放電(改)
どうも,間違いを修正してみました.これなら,つじつまが合いそうです.
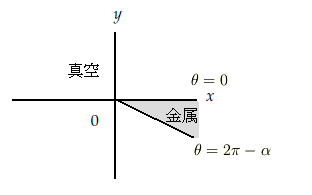
電荷が作る電場は,尖ったものの先端において,大きくなり 電子を放出しやすくなります.どんな電界が生じるのかを 書くことにします.
簡単のため,下図の様な二次元極座標 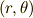 で考えます.
クサビ型の金属で奥行きを
で考えます.
クサビ型の金属で奥行きを  方向としてもらって構いません.
金属表面は等電位面であります.しかし,表面電荷はそんざいします.
方向としてもらって構いません.
金属表面は等電位面であります.しかし,表面電荷はそんざいします.
真空におけるラプラス方程式は,
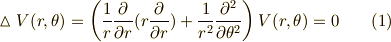
ここで,変数分離法を用い,  方向と
方向と 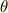 方向の常微分方程式に還元してやります.
つまり,
方向の常微分方程式に還元してやります.
つまり, 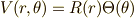 と仮定して,式
と仮定して,式 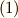 に代入するのです.
すると,
に代入するのです.
すると,
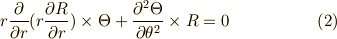
両辺 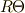 で割って,移項すれば,
で割って,移項すれば,
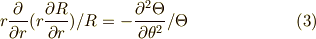
これは,左辺が  のみの関数,右辺が
のみの関数,右辺が 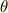 のみの関数なので,
のみの関数なので,  の式ではなく,
の式ではなく, 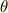 の式でもなく,
これは実定数
の式でもなく,
これは実定数 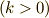 の二乗
の二乗 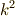 [*] に等しいことが分かります.
[*] に等しいことが分かります.
| [*] | 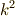 が負だと が負だと  方向の方程式が,虚数の解をもつことになるので,物理的に意味のない方程式になります. 方向の方程式が,虚数の解をもつことになるので,物理的に意味のない方程式になります. |
よって,この式は,

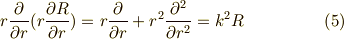
式 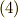 は,単振動でお馴染みの式ですね.これをとくと,
は,単振動でお馴染みの式ですね.これをとくと,

境界条件 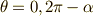 の時,
の時, 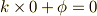 ,
, 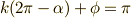 とします.つまり,
とします.つまり, 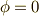 ,
, 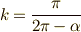 となります.
となります.
これで, 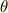 方向は解けました.次は動径方向です.
方向は解けました.次は動径方向です. 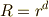 と仮定すると,式
と仮定すると,式 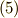 より,
より,
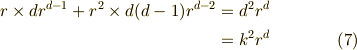
よって, 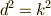 が得られます.正負の符号の内,
信じられないかもしれませんが,無限遠で発散する
が得られます.正負の符号の内,
信じられないかもしれませんが,無限遠で発散する 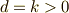 が求める解であります.
これは,原点近傍のみで有効であります.
この正の解を取る理由としては,例えば,
が求める解であります.
これは,原点近傍のみで有効であります.
この正の解を取る理由としては,例えば, 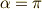 の時を考えてください.
xy平面の下半分が金属という状態です.この時,
の時を考えてください.
xy平面の下半分が金属という状態です.この時,  となり,
本来,平面状の一様な面電荷が作る電場は,面に垂直で距離を変えても一定の大きさとなりますよね.
つまり,例えばポテンシャルとしては,
となり,
本来,平面状の一様な面電荷が作る電場は,面に垂直で距離を変えても一定の大きさとなりますよね.
つまり,例えばポテンシャルとしては, 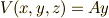 のような形をしています.
よって,ここで
のような形をしています.
よって,ここで 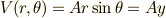 となります.
これは,
となります.
これは, 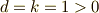 とすれば,見事に,
とすれば,見事に,
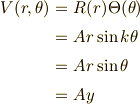
となる訳です.ここで, 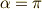 だった,
クサビの尖り具合をしめす
だった,
クサビの尖り具合をしめす 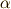 は,連続的変化で
は,連続的変化で 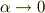 となれますから,
結局,
となれますから,
結局, 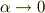 とした時,
とした時,
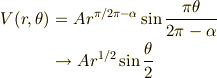
となり,原点近傍において 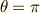 の方向に,
の方向に, 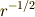 の大きさの,電場の発散が起きることが分かります.
これが,尖ったものが静電気を放電しやすい原理です.
の大きさの,電場の発散が起きることが分かります.
これが,尖ったものが静電気を放電しやすい原理です.
それでは,今日はここまで.