ファラデー効果
掲示板で要望があったので書いてみました. ファラデー効果とは,「分極を起こす物質に磁場をかけると,その磁場に平行な方向に進む 直線偏光光は,その偏光方向が回転していく.」という現象です. それを古典振動子モデルで説明します.
物質中のマクスウェル方程式
これから,物質中のイオンに束縛される電子の運動方程式を考えたいのですが,その前に物質中の物理量の 満たす関係式を復習しておきます.
電場  と電束密度
と電束密度 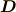 ,分極
,分極 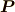 の間には,
の間には,

という関係が,
磁場 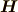 と磁束密度
と磁束密度 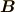 ,磁化
,磁化 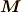 の間には,
の間には,
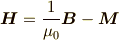
これは物質の透磁率  を用いて,
を用いて,
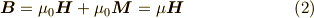
という関係が成り立ちます.
一方,マクスウェル方程式は,原子に束縛されていない自由な電荷を添え字の 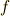 で表わすと,
で表わすと,

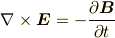
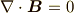
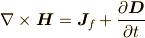
今回は,物質中の自由な電荷はなく,かつ,磁化は弱いと考え無視します. よって,扱うマクスウェル方程式を書きなおすと,




式 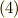 に
に  を施して,式
を施して,式 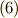 を利用すると,
を利用すると,
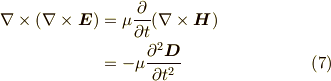
この式の左辺は,
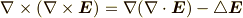
のように変形出来るので,結局,式 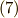 は,
は,

となります.
この式  は,左辺第一項がなければ波動方程式になります.
実はこの節を書いたのは,式
は,左辺第一項がなければ波動方程式になります.
実はこの節を書いたのは,式  をあとで使うことになるからです.
この式は重要ですので,こういう式があったな程度には覚えておいてください.
をあとで使うことになるからです.
この式は重要ですので,こういう式があったな程度には覚えておいてください.
振動子と光のの古典的モデル
少々長いので,何をしたいかを簡潔に話しておくと,  と
と 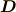 の間の関係を求めて
式
の間の関係を求めて
式  に代入したいのです.
に代入したいのです.
さて,下の図のように透明な物質にコイルを巻き磁場Bを作り,そこに直線偏光の光を 磁場と平行に入射することを考えます.

ここで,物質中の正イオン(原子核)に束縛された最外殻電子について考えます. 古典的な運動方程式は,下の様なモデルで考えることができます. 座標は,磁場の方向をz軸,上方向をy軸,画面手前方向をx軸とする右手系とします.
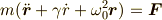
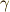 は正の値を持つ摩擦による減衰項,
は正の値を持つ摩擦による減衰項, 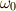 はイオンとの引力が作る復元力の角振動数
です.
はイオンとの引力が作る復元力の角振動数
です. 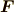 は外力であり,
今回の場合,
は外力であり,
今回の場合, 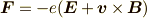 となります.
となります.
成分ごとに式を書いてみます.

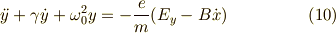

z方向には特別な動きがないことがわかります.議論の中心となるのは,xy平面での運動です. この方程式を扱うちょっとしたテクニックがあります. 現在,二変数が二つの式にちらばっていますが,ふたつの式の線形結合をとることによって, 独立な一変数の式,ふたつに変えるのです. それには線形代数の対角化を利用します.
演算子を  と書き,あたかも係数のように書くことができます.
と書き,あたかも係数のように書くことができます.
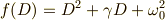
とすると,
式 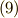 ,
, 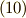 は,行列を用いて,
は,行列を用いて,
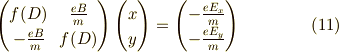
これを対角化すれば,うまく変数をまとめることができます. 上の式の二次正方行列をAとすると,
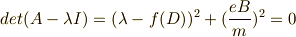
より,
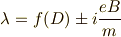
ここで,式  に左から二次の行ベクトルをかけることは,式
に左から二次の行ベクトルをかけることは,式 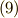 ,
, 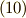 の
線形結合をとることに対応します.よって,あまり聞きなれませんが,
今回求めるのは,Aの固有行ベクトルを求めればいいことになります.
の
線形結合をとることに対応します.よって,あまり聞きなれませんが,
今回求めるのは,Aの固有行ベクトルを求めればいいことになります.
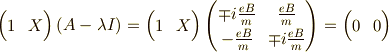
をみたすのは,
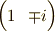
であることが分りました.これから 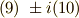 を作ると,確かに,
を作ると,確かに,
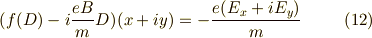
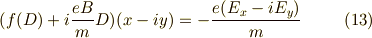
となって,きれいにまとめることができました.
特解と一般解
これをまともに解くのは大変なので,定性的な説明をしておきます.
この微分方程式は,式 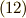 ,
, 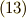 の右辺をゼロとした式を斉次方程式といい,
その解を一般解といいます.一般解の線形結合は,やはり一般解です.
の右辺をゼロとした式を斉次方程式といい,
その解を一般解といいます.一般解の線形結合は,やはり一般解です.
そして,右辺がゼロでない場合,その方程式は非斉次方程式といわれ, その解の一つを特解といいます.この方程式のすべての解は,一般解の線形結合+特解 で尽くされます.
今回の場合,式 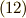 ,
, 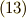 の右辺が振動項で,
右回り円偏光 [*]
の右辺が振動項で,
右回り円偏光 [*] 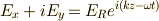 の時や,
左回り円偏光
の時や,
左回り円偏光  の時を考えます.
の時を考えます.
| [*] | なぜ円偏光と言えるのか考えてみましょう.右回りの場合,電場が実数であることを考えれば,オイラーの公式  より, より, 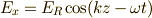 かつ かつ 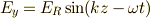 となり,z=一定の場所で変化を追うと,進行方向に向かって右回りであることがわかります. となり,z=一定の場所で変化を追うと,進行方向に向かって右回りであることがわかります. |
非斉次項が振動項の場合,この方程式の解はどんな初期条件であっても, 時間がたつと振動項に対応する定常応答に落ち着きます.
一方,一般解は大きさが指数関数的に減少する項であり減衰項と呼ばれます. これは初期条件から定常応答に移行する際のつじつま合わせの役割をします.
以降,定常応答だけを考えます.
右回り円偏光の入射(rとEの関係)
まず,右回り偏光 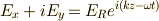 の時だけ考えます.
の時だけ考えます.
このとき,複素共役を  で表わすと,
で表わすと, 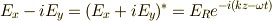 となりますから,式
となりますから,式 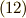 については,
については, 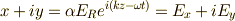 が定常応答になり,
その結果,微分演算子
が定常応答になり,
その結果,微分演算子 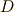 を複素数
を複素数 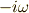 で置き換えることができます.
で置き換えることができます.
一方,式 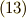 については,
については,  が定常応答になり,
こっちの式では,微分演算子
が定常応答になり,
こっちの式では,微分演算子 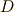 を複素数
を複素数 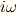 で置き換えることができます.
で置き換えることができます.
 も
も 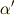 も複素数であることに注意してください.
も複素数であることに注意してください.
書きなおすと式 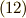 は,
は,
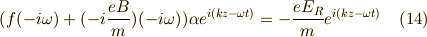
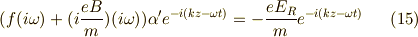
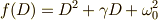 を代入してやると,
を代入してやると,
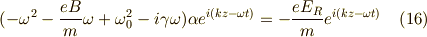

となり,  を実数として,
を実数として,
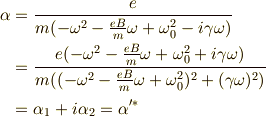
- ひとつ注意しておくと,
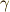 がゼロ(抵抗力が働かない)時は,
がゼロ(抵抗力が働かない)時は, 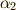 がゼロとなり,
がゼロとなり,  が実数になります.
が実数になります.
ですから, 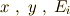 はすべて実数であることを考慮すると,
式
はすべて実数であることを考慮すると,
式 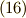 ,
, 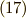 は,どちらか一つだけで十分な意味を持ち,
以下のように,
は,どちらか一つだけで十分な意味を持ち,
以下のように,
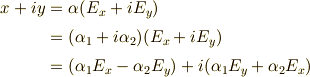
を実部,虚部に分離できて,
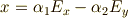
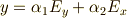
左回り円偏光の入射(rとEの関係)
左回り円偏光についても同様に,こんどは,
 の時を考えます.
式
の時を考えます.
式 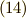 に対応する式は,
に対応する式は,
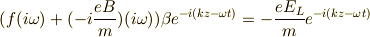
ですから,
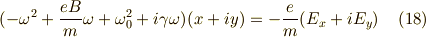
となり, 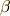 は以下のようになり,
は以下のようになり,
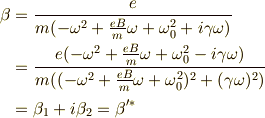
結局,位置  と電場
と電場  の関係は,
の関係は,
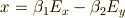
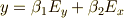
となります.
電束密度D,分極P,電場Eの関係
分極 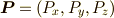 は,
は, 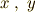 に
に 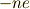 を掛けたものであり,
を掛けたものであり,

となりますから,まず右回り偏光の時は,
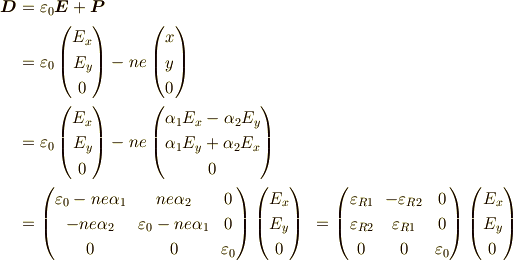
これで,やっと式  が利用できます.
が利用できます.
電場 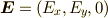 と進行方向
と進行方向 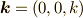 は垂直なので,
は垂直なので,
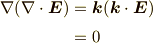
ですから,式  は,以下のように波動方程式になります.
は,以下のように波動方程式になります.
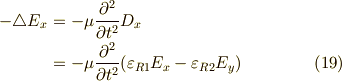
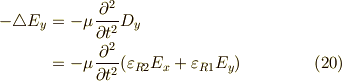
さっき行った対角化の方法によると,
式について, 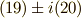 をとれば,二つの共役な式が出てきて,一方だけを書くと,
をとれば,二つの共役な式が出てきて,一方だけを書くと,
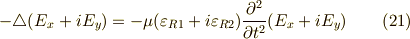
右回り偏光なので, 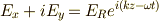 を代入すると,
分散関係が出てきます.
を代入すると,
分散関係が出てきます.
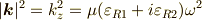
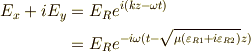
この式は, 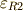 がノンゼロの時減衰することが解ります.
つまり,それは抵抗項
がノンゼロの時減衰することが解ります.
つまり,それは抵抗項 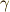 がノンゼロの時を表しますから,
電子に抵抗があると光は減衰しながら伝わっていくことになり,
物理的感覚に合っています.
がノンゼロの時を表しますから,
電子に抵抗があると光は減衰しながら伝わっていくことになり,
物理的感覚に合っています.
左回り円偏光の場合は,前は  に対応して
に対応して  が決定されたのに対し,
が決定されたのに対し,
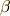 に対応して
に対応して  が決定されます.その分散関係は,
が決定されます.その分散関係は,
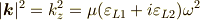
であり,

ここまで来て注目するべきところは,
抵抗項  がゼロの時を考えると,
光の振動数
がゼロの時を考えると,
光の振動数  が同じでも,右回り円偏光と左回り円偏光で,
波数kが異なってくることです.
が同じでも,右回り円偏光と左回り円偏光で,
波数kが異なってくることです.
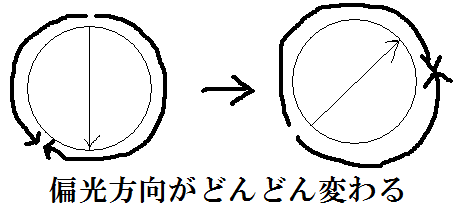
直線偏光は,右回りと左回りの円偏光の重ね合わせと考えられますから, その二つの偏光の波数が異なるということは,位置と共に波の位相がずれていく, つまり,直線偏光の方向が,異なってくるということになります.
余談
今回の話は,磁場によるローレンツ力という,速度に垂直に働く力が原因です. そういえば,フーコーの振り子もコリオリ力という速度に垂直に働く力が原因で, 振り子の回転方向が回転していく現象なので,方程式としては似ているなと思いました.