クリフォード代数とマクスウェル方程式
2020.03.29追記 うべさんがブログを作りました.ご興味ある方は こちらから どうぞ!
最近,Twitterで知り合った高専生のうべゆうとさんという方に 真空中のマクスウェル方程式の面白い表現を教えていただいたので, それについて述べてみようと思います. クリフォード代数というものを使います. 実に興味深いです.結論から言うと,マクスウェル方程式は たった一本の方程式として表現でき,

となります,ここで, 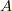 と
と 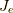 は4元ポテンシャルと4元電流密度
は4元ポテンシャルと4元電流密度
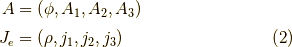
であり, 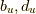 は微分演算子の一種で,微分形式で使う外微分
は微分演算子の一種で,微分形式で使う外微分 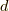 と同じ記号なので,
この記事では僕がうべさんの"u"をお借りして
と同じ記号なので,
この記事では僕がうべさんの"u"をお借りして 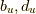 と書くことにします.
これをうべさんはそれぞれ右純然微分作用素,左純然微分作用素と名付けました.
と書くことにします.
これをうべさんはそれぞれ右純然微分作用素,左純然微分作用素と名付けました.
クリフォード代数の基本
クリフォード代数はその基底の二乗の値に 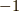 を許容する代数です.
複素数の拡張と考えられます.今回我々が使うのは,
四つの基底
を許容する代数です.
複素数の拡張と考えられます.今回我々が使うのは,
四つの基底 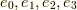 に対して,
に対して,
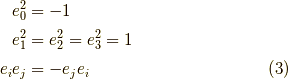
を満たすものです.クリフォード代数では 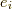 の二乗は実数にグレードダウンできますが,
最後の式から,
の二乗は実数にグレードダウンできますが,
最後の式から, 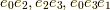 等は消えずにその形で残ります.
また,この代数は非可換です.
等は消えずにその形で残ります.
また,この代数は非可換です.
そして,クリフォード代数の商を例えば,次の様に考えます.実数  に対して,
に対して,
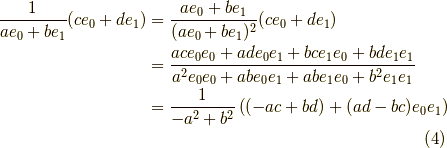
となります.逆数を右から掛けるか左から掛けるかで結果が変わることにご注意ください.
すると,この代数は逆元を 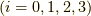 に対して
に対して 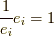 で定義する,つまり,
で定義する,つまり,
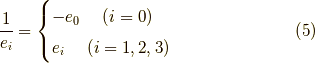
とすれば良いです.
うべさんの発見
僕がうべさんから教えていただいた時には,発見論的な話で聞いたのですが, 紆余曲折は本質を見づらくすると思うので,結論に直接持っていく話をしようと思います.
偏微分微分演算子の記号 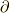 を右に作用するか左に作用するかで
を右に作用するか左に作用するかで 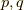 とします.
つまり,
とします.
つまり,
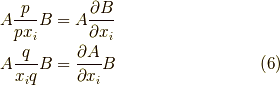
とします.余談ですが,右と左で対称的な作用をすることから,
左右で対称な記号の対として  を
選んだそうです.
を
選んだそうです.  は,partial differential の
は,partial differential の  だったり,
彼の尊敬するDiracから
だったり,
彼の尊敬するDiracから 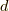 を選んだともおっしゃっていました.
こういう遊び心は良いですね.
を選んだともおっしゃっていました.
こういう遊び心は良いですね.
そして,いよいよこの記事の冒頭で書いた記号 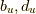 を定義します.
その定義は
を定義します.
その定義は
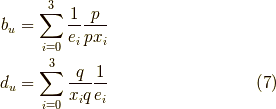
とします.
マクスウェル方程式のクリフォード代数での記述
自然単位系,つまり  とした(今回は
とした(今回は 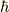 は使いませんが)
真空中のマクスウェル方程式を書くと
は使いませんが)
真空中のマクスウェル方程式を書くと
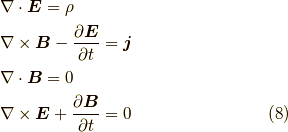
となります.ポテンシャルを 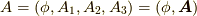 とすれば,
とすれば,
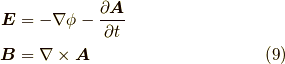
となります.ここで, 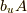 を計算してみます.すると,
を計算してみます.すると,
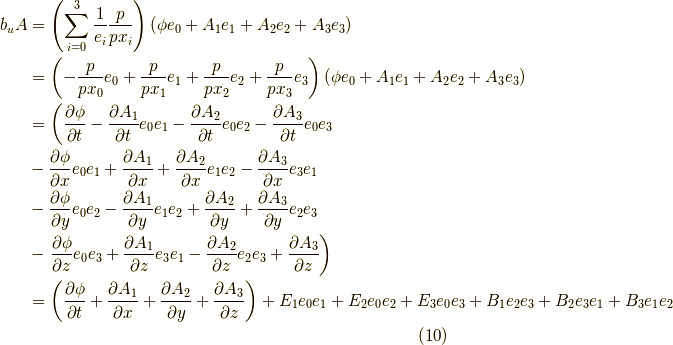
最後の行に行くには,式 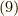 を使いました.
同様に
を使いました.
同様に 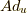 を計算すると,
を計算すると,
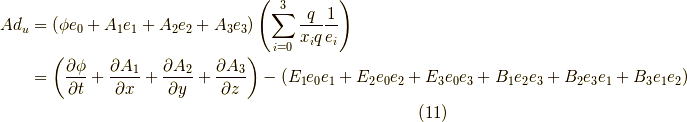
となります.マクスウェル方程式の登場人物が出てきましたね.  です.さらにもう一歩進んで,
です.さらにもう一歩進んで,
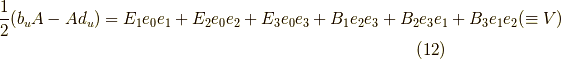
とします.(  は
は 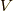 をこれで定義するという意味です.)
ここで,左からさらに
をこれで定義するという意味です.)
ここで,左からさらに 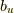 を掛けると,
を掛けると,

これを

と書いても誤解は生じないでしょう. 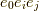 は上から順に
は上から順に 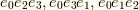 を表します.
を表します.
すると,これはマクスウェル方程式の左辺になっています.つまり,後は電流密度を 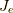 として,
として,

とすれば,式 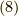 の事を
の事を

と書けるのです.
また,もし磁気モノポールが存在するなら,
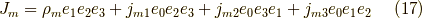
によって,マクスウェル方程式を,

と書けます.右辺の符号が気になるなら,

としても良いです.
最後にうべさんの上げた成果について,述べておきます.
この記事は,うべさんのレビューを基にクロメルが作ったレビューであり,
新規性はどこにあるかと言うと,実をいうと古くから知られていたことを表現しなおしたことの域を得ません.
また,左右の純然微分作用素に関しては,ウェッジ積を用いた同様のものは以前から存在しているらしいです.
しかし,分母に 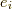 を持ってきたことは,うべさんが初めてではないかと思われます.
もし,この辺りの事情に詳しい方がいらっしゃったら, クロメル までメールでご一報ください.
うべさんは現在,現役の高専生ということで(若い!),将来がとても楽しみです.
を持ってきたことは,うべさんが初めてではないかと思われます.
もし,この辺りの事情に詳しい方がいらっしゃったら, クロメル までメールでご一報ください.
うべさんは現在,現役の高専生ということで(若い!),将来がとても楽しみです.
うべさん,面白い話をありがとうございました.今日はここまで,お疲れさまでした.