コンデンサーの過渡現象
コンデンサを充電すると電荷 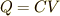 が蓄えられるというのは,高校の電気の授業で最初に習います.
しかし,充電される途中で何が起こっているかについては詳しく習いません.
このような充電中のできごとを 過渡現象 (かとげんしょう)と呼びます.
ここでは,コンデンサーの過渡現象について考えていきます.
が蓄えられるというのは,高校の電気の授業で最初に習います.
しかし,充電される途中で何が起こっているかについては詳しく習いません.
このような充電中のできごとを 過渡現象 (かとげんしょう)と呼びます.
ここでは,コンデンサーの過渡現象について考えていきます.
回路方程式
次のような,抵抗値 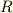 の抵抗と,静電容量
の抵抗と,静電容量 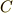 のコンデンサからなる回路を考えます.
のコンデンサからなる回路を考えます.
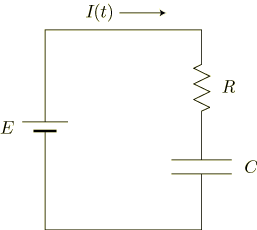
まずは回路方程式をたててみましょう.時刻 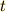 においてコンデンサーの極板にたまっている電荷量を
においてコンデンサーの極板にたまっている電荷量を 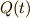 ,電池の起電力を
,電池の起電力を 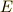 とします. [1]
電流と電荷量の関係は
とします. [1]
電流と電荷量の関係は 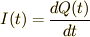 で表されるので,抵抗での電圧降下は
で表されるので,抵抗での電圧降下は 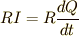 ,コンデンサーでの電圧降下は
,コンデンサーでの電圧降下は 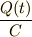 です.
キルヒホッフの法則から回路方程式は
です.
キルヒホッフの法則から回路方程式は
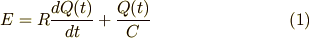
となります.
| [1] | 電池の起電力 - 電池に電流が流れていないときの,その両端子間の電位差をいいます. |
回路方程式を解く
では回路方程式 (1) を,初期条件 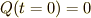 のもとに解いてみましょう.
これは変数分離型の一階線形微分方程式ですので,以下のようにして解くことができます.
のもとに解いてみましょう.
これは変数分離型の一階線形微分方程式ですので,以下のようにして解くことができます.
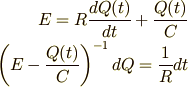
これを積分すると,
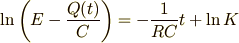
となります.ここで 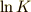 は積分定数です.
は積分定数です.
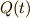 について解くと,
について解くと,
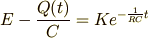
より,
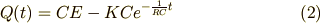
となります.
初期条件 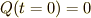 から,積分定数
から,積分定数 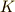 を決めてやると,
を決めてやると, 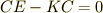 より
より 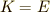 であることがわかります.
したがって,コンデンサにたまる電荷量
であることがわかります.
したがって,コンデンサにたまる電荷量 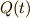 は
は
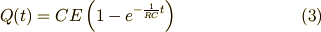
となります.グラフに描くと次のようになります.
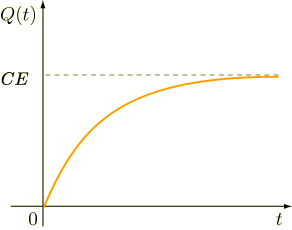
また,(3)式を微分して電流 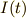 も求めておきましょう.
も求めておきましょう.
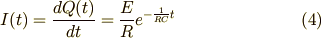
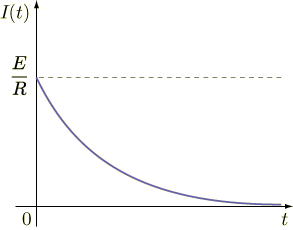
電流のグラフも描くと次のようになります.
消えたエネルギー

ところで私たちは高校の授業で,上のような回路を考えたときに電池のする仕事  は
は 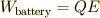 であると公式として習いました.
であると公式として習いました.
いっぽう,コンデンサーが充電されて,電荷 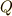 がたまったときのコンデンサーがもつエネルギー
がたまったときのコンデンサーがもつエネルギー 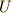 ( 静電エネルギー といいました)は,
( 静電エネルギー といいました)は,
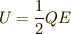 であると習っています.
であると習っています.
電池がした仕事が 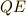 ,コンデンサーに蓄えられたエネルギーが
,コンデンサーに蓄えられたエネルギーが 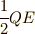 .
全エネルギーは保存するはずです.あれ?残りの
.
全エネルギーは保存するはずです.あれ?残りの 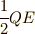 はどこに消えたのでしょうか?
はどこに消えたのでしょうか?
謎解き
さて,この謎を解くために,電池のする仕事について詳しく考えてみましょう.
起電力 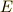 を持つ電池は,電荷を電位差
を持つ電池は,電荷を電位差 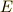 だけ汲み上げる能力をもちます.
この電池が微少時間
だけ汲み上げる能力をもちます.
この電池が微少時間 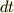 に電荷量
に電荷量 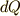 だけ電荷を汲み上げるときにする仕事
だけ電荷を汲み上げるときにする仕事 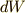 は
は

です.(4)式の両辺を単純に積分すると

という関係が得られます.
したがって,電池が 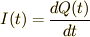 の電流を流すときの仕事率
の電流を流すときの仕事率 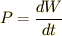 は (4)式より
は (4)式より
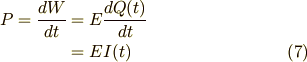
となります.
さて,電池のした仕事がどうなったのかを,回路方程式 (1) をもとに考えてみましょう.
回路方程式 (1)式の両辺に,電流 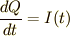 をかけてみます.
をかけてみます.
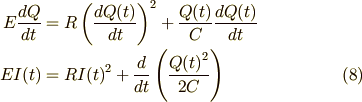
左辺が(6)式の仕事率の形になりました.
両辺を時間 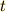 で
で 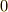 から
から 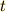 まで積分します.初期条件は
まで積分します.初期条件は 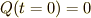 でしたので,
でしたので,
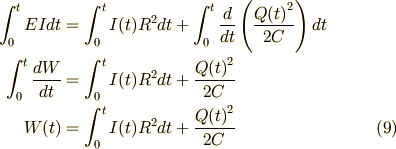
となります.この式は,左辺が 電池のした仕事 ,右辺の第一項が時刻 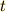 までに発生した ジュール熱 ,右辺第二項が(時刻
までに発生した ジュール熱 ,右辺第二項が(時刻 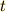 で) コンデンサーのもつエネルギー です.
で) コンデンサーのもつエネルギー です.
(7)式において 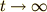 の極限を考えると,電池が過渡現象を経てした仕事
の極限を考えると,電池が過渡現象を経てした仕事  は最終的にコンデンサに蓄えられた電荷
は最終的にコンデンサに蓄えられた電荷 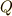 を用いて
を用いて
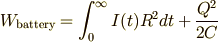
と書けます.過渡的状態を経て平衡状態になると,コンデンサーと電圧と電荷量の関係式 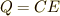 が使えるので右辺第二項に代入して
が使えるので右辺第二項に代入して
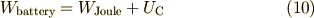
となります.ここで 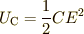 は静電エネルギー,
は静電エネルギー, 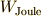 は平衡状態に至るまでに抵抗で発生したジュール熱で,
は平衡状態に至るまでに抵抗で発生したジュール熱で,
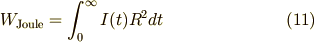
です.(11)式に先ほど求めた(4)式の電流 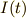 を代入すると,
を代入すると,
![W_{\text{Joule}} & = \int_0^{\infty} \frac{E^2}{R} e^{-\frac{2}{RC} t} dt \\ & = \frac{E^2}{R} \left[ - \frac{RC}{2} e^{-\frac{2}{RC} t} \right]_0^{\infty} \\ & = \frac{1}{2} CE^2 \tag{12}](./7bfef65db647c6e42f2d7b27dc8febf7.png)
となります.
結局どういうことか?
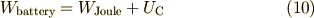
上の謎解きから,電池のした仕事 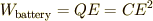 は,回路の抵抗で発生したジュール熱
は,回路の抵抗で発生したジュール熱 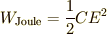 と
コンデンサに蓄えられたエネルギー
と
コンデンサに蓄えられたエネルギー 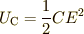 に化けていたということが分かりました.
つまりエネルギー保存則はきちんと成り立っていたわけです.
に化けていたということが分かりました.
つまりエネルギー保存則はきちんと成り立っていたわけです.
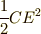 だけ発生します.
つまり過渡状態から平衡状態になるまでに, 必ず 電池がした仕事の半分だけジュール熱が発生するということです.
だけ発生します.
つまり過渡状態から平衡状態になるまでに, 必ず 電池がした仕事の半分だけジュール熱が発生するということです. があります.
があります. 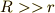 なので
なので