電磁場のローレンツ変換
この記事では速度と力のローレンツ変換を既知として,
電場 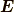 と磁束密度
と磁束密度 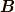 のローレンツ変換を求めます.
のローレンツ変換を求めます.
想定する状況と前提知識
速度のローレンツ変換
まず,慣性系の一つK系を考えます.
次にx軸方向に 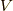 の速度で動く別の慣性系K'系を考えます.
また,粒子がK系では
の速度で動く別の慣性系K'系を考えます.
また,粒子がK系では 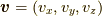 で動いているものとし,
K'系ではその粒子が
で動いているものとし,
K'系ではその粒子が 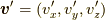 で動いているとします.
で動いているとします.
この時, 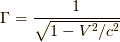 として,
として,
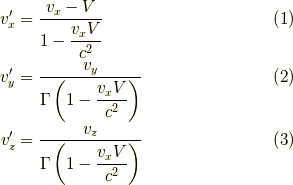
の関係があります.
力のローレンツ変換
運動方程式は,次の様になります.

ただし, 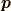 は四元運動量の空間成分,
は四元運動量の空間成分, 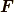 は力です.
K系での粒子の速度を
は力です.
K系での粒子の速度を  ,
, 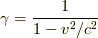 とすると,
とすると,
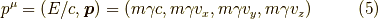
となります.K'系で力を 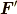
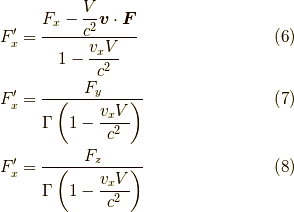
と言う関係があります.
電磁場のローレンツ変換
x軸方向の成分の変換
さて,K系,K'系を同様に設定して,電荷 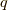 の荷電粒子
の荷電粒子 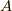 がK系に対して
がK系に対して  軸方向に
軸方向に 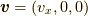 で運動しているとしても一般性は失われません.(最後の結論を見ていだければ明らかです.)
で運動しているとしても一般性は失われません.(最後の結論を見ていだければ明らかです.) 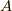 に働く電磁気力は
に働く電磁気力は
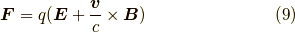
です.物理法則は不変なはずなので, これをK'系で見ると,
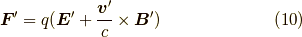
となります.式 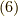 から力のの変換則は
から力のの変換則は 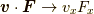 から,
から,
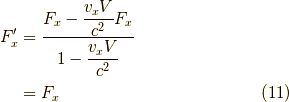
となるので,

より,

となります.x軸方向については 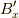 と
と 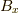 の関係も欲しいのですが,
どう求めて良いか分かりませんでした.荷電粒子は運動方向の磁束密度とは相互作用を起こさない為です.
参考文献には
の関係も欲しいのですが,
どう求めて良いか分かりませんでした.荷電粒子は運動方向の磁束密度とは相互作用を起こさない為です.
参考文献には

とあります.
z軸方向の成分の変換
まずは, 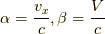 とします.この時,式
とします.この時,式 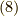 より,
より,
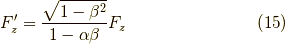
となります.よって,
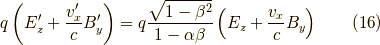
となり,式 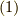 から,
から,

ですから,式 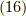 を書き直すと,
を書き直すと,
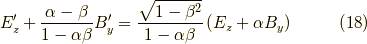
となります.
ここで,式 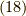 の自由度を落とすため,
の自由度を落とすため, 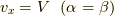 の時を考えます.
すると,
の時を考えます.
すると,
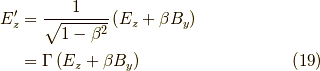
が得られます.(ここでさりげなく  を
を 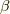 に置き換えていますが,これは
に置き換えていますが,これは 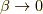 の極限でロ−レンツ力を再現するようにしています.)次に,
の極限でロ−レンツ力を再現するようにしています.)次に, 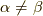 の時を考えると,
の時を考えると,
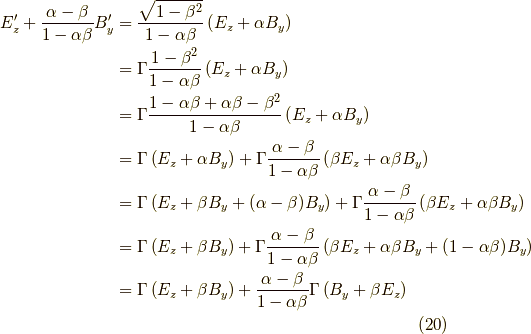
ここで, 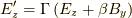 でしたから,
でしたから,
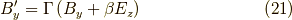
が求まりました.
y軸方向も同様に求められます.以上をまとめると,
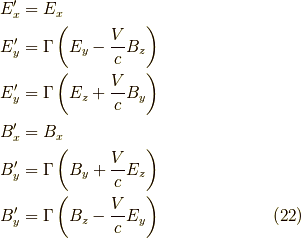
となります.これは  軸方向の運動でしたから,
一般には,運動方向に平行な成分を
軸方向の運動でしたから,
一般には,運動方向に平行な成分を  ,垂直な成分を
,垂直な成分を 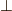 とすると,
とすると,
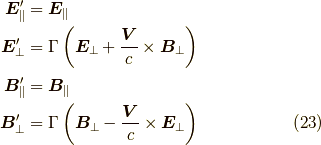
となります.今日はここまで.お疲れさまでした.