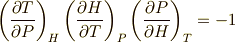微分形式の熱力学への応用
微分形式の理論を熱力学に応用してみます.途中の議論にも結果にも,何にも新しい話は出てきませんので,外微分の計算練習だと思って気楽に呼んでください.少し熱力学の勉強をしたことがあることが望ましいです.
熱力学第一法則
熱力学第一法則は,微分形で次のように書かれました.

式中, 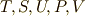 はそれぞれ,系の温度,エントロピー,内部エネルギー,圧力,体積を意味するとします.ところで,私達は式
はそれぞれ,系の温度,エントロピー,内部エネルギー,圧力,体積を意味するとします.ところで,私達は式 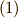 を一次微分形式と見ることもできます!!両辺の外微分を取ると,次の二次微分形式を得ます.
を一次微分形式と見ることもできます!!両辺の外微分を取ると,次の二次微分形式を得ます.  に注意して下さい.
に注意して下さい.
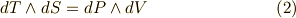
熱力学第一法則の自由度は基本的に 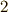 ですので,式
ですので,式 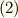 をどのような二次元座標系で表現するか,というのが一つ目の問題です.(つまり,独立変数は二つで,残りの二つは関数だと言うことです.)
をどのような二次元座標系で表現するか,というのが一つ目の問題です.(つまり,独立変数は二つで,残りの二つは関数だと言うことです.)
| [*] | 少し発展的な註になりますが,式 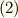 は二次元多様体上の微分形式と考えることが出来ます. は二次元多様体上の微分形式と考えることが出来ます. 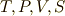 等が,この多様体上の関数(零次微分形式もしくは座標関数)になります.いまは多様体という言葉を聞いたことがない人もいると思いますが,もうすぐ勉強しますので,そのときまたこの記事を思い出してみて下さい. 等が,この多様体上の関数(零次微分形式もしくは座標関数)になります.いまは多様体という言葉を聞いたことがない人もいると思いますが,もうすぐ勉強しますので,そのときまたこの記事を思い出してみて下さい. |
色々試してみましょう.まず 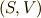 座標系を取り,
座標系を取り, 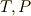 は
は 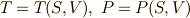 とします.このとき,式
とします.このとき,式 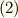 は次のように変形できます.括弧の右下の添字は,一定に保たれる変数を意味します.例えば
は次のように変形できます.括弧の右下の添字は,一定に保たれる変数を意味します.例えば 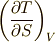 は,『
は,『 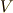 一定の場合の,
一定の場合の, 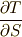 』という意味です.熱力学で,よく使う記法です.
』という意味です.熱力学で,よく使う記法です.
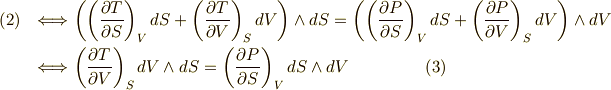
これより,次式を得ます. 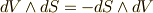 が効いてます.
が効いてます.

これは マックスウェルの関係式 と呼ばれる熱力学的関係式の一つです.
もっと関係式を
他にも熱力学的関係式を導くことが出来ます.式 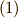 の両辺を
の両辺を  で割ります.
で割ります.

この両辺の外微分を取ります.
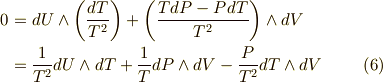
ここで,ふたたび 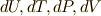 のうち,独立なものを二つ選びます.
のうち,独立なものを二つ選びます. 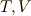 を選んで
を選んで 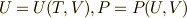 とすると,式
とすると,式  は次のように変形できるでしょう.
は次のように変形できるでしょう.
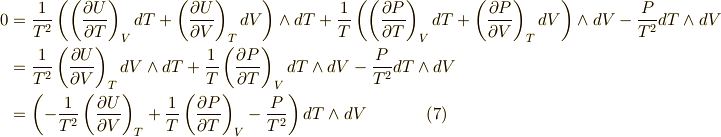
式 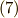 より,最後の行の括弧が
より,最後の行の括弧が 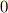 になることが要請され,
になることが要請され, 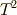 を両辺に掛けて次式を得ます.
を両辺に掛けて次式を得ます.
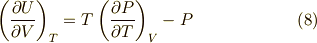
式 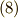 には特別な名前は無いと思いますが,これも熱力学の重要な公式です.(熱力学の教科書のどこかに必ず載っていると思います.)
には特別な名前は無いと思いますが,これも熱力学の重要な公式です.(熱力学の教科書のどこかに必ず載っていると思います.)
発展
最後にもう一つだけ重要な公式を導いておきます.変数 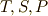 は,変数を巡回的に次のように表現できます.
は,変数を巡回的に次のように表現できます.



これらは二次元空間上の量なので,自由度は 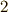 です.このとき,次のような関係式を導くことができます.
です.このとき,次のような関係式を導くことができます.
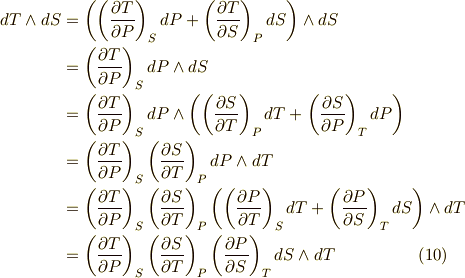
この両辺を比べて,次式を得ます.
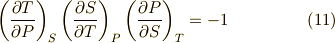
これも熱力学では重要な公式です.
発展的な補足
式 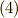 から残りのマックスウェルの関係式を導くとき, ルジャンドル変換 という操作を使って,変数を入れ替えていく方法を勉強した人もいると思います.微分形式を知っているみなさんは,
から残りのマックスウェルの関係式を導くとき, ルジャンドル変換 という操作を使って,変数を入れ替えていく方法を勉強した人もいると思います.微分形式を知っているみなさんは,  などを,何らかの二次元空間上で一次微分形式の基底になっていると見ることが出来ると思いますが,はたしてこの空間(つまり式
などを,何らかの二次元空間上で一次微分形式の基底になっていると見ることが出来ると思いますが,はたしてこの空間(つまり式  が定義される空間)がどんな空間なのか,私達は全然知りません.幾何学的には,
が定義される空間)がどんな空間なのか,私達は全然知りません.幾何学的には, 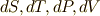 のうち二つの変数が形づくる曲面だと考えられますが,直観的に想像できるものはないと思います.しかし,少なくとも普通のユークリッド空間ではない,という予感はします.
のうち二つの変数が形づくる曲面だと考えられますが,直観的に想像できるものはないと思います.しかし,少なくとも普通のユークリッド空間ではない,という予感はします.
そこで,空間の概念を拡張した,二次元多様体という集合をそのうちを考えることになります.この集合に含まれる点は,どの点を選んでも,その近傍が局所的に二次元ユークリッド空間になっており,二次元座標を導入することが出来るのですが,大局的な性質は分からなくても良いのです.(多様体として,まずは連続的な集合を考えているので,何か三次元的な図形だと思って良いです. 多様体の概念 を参考にして下さい.)局所的な基底の取り方は色々ある訳ですが,一次微分形式は,多様体上では 余接ベクトル というものになっています.名前は,今のところ気にしなくて大丈夫です.このような幾何学的な見方を推し進めてみると,ルジャンドル変換とは,多様体上での座標変換に他ならなかったことが分かります.多様体はまだ勉強してないので,ここに書いた内容が全然分からなくても,いまは大丈夫です.多様体は座標系や座標変換に関して,より広い視野を与えてくれる概念で,もうすぐ勉強します.
| [†] | さらに言えば,ルジャンドル変換で考える多様体は,シンプレティック多様体という,多様体の概念をパワーアップさせたものになります.著者も正直よく分かっていないのですが,そんな話まで一緒に勉強できればいいと思っています. |
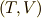 ,
, 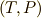 ,
, 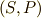 などの取り方を試すことで,マックスウェルの関係式の残りの三つも求めてみて下さい.
などの取り方を試すことで,マックスウェルの関係式の残りの三つも求めてみて下さい.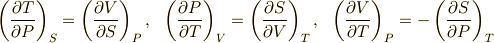
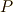 で割る形からスタートし,次の公式を導いてみて下さい.
で割る形からスタートし,次の公式を導いてみて下さい.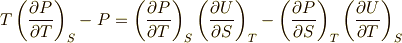
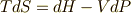 を出発点にして,次の公式を求めてみて下さい.
を出発点にして,次の公式を求めてみて下さい.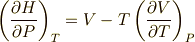
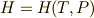 を使い,次の公式を求めてみましょう.
を使い,次の公式を求めてみましょう.