ポアンカレの補題
標題のポアンカレの補題とは直接関係ないのですが,まず外微分についての次の重要な定理を証明します.
外微分に対して,一般に次の関係が成り立ちます.
theorem
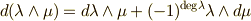
これは,外微分における『積の微分』とも言うべき公式ですが,符号に特に注意が必要です. 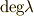 は,微分形式
は,微分形式 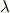 の次数を表わすとします.証明は,結構面倒くさいです(・_・).
の次数を表わすとします.証明は,結構面倒くさいです(・_・).
proof
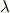 を
を 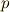 次微分形式,
次微分形式, 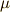 を
を 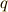 次微分形式とし,
次微分形式とし, 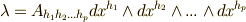 ,
, 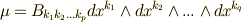 と置きます.ただし,
と置きます.ただし, 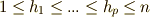 ,
, 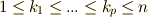 とします.
とします.  は
は  次微分形式になりますので,基底を一個増やして
次微分形式になりますので,基底を一個増やして 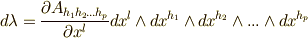 と書けます.ただし,右辺は縮約によって和の形になっているとします.基底には
と書けます.ただし,右辺は縮約によって和の形になっているとします.基底には 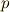 個の
個の  が含まれますので,
が含まれますので, 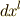 を一番右に持っていき,
を一番右に持っていき, 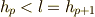 と置くことで次のように書けます.
と置くことで次のように書けます. 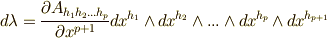 .この関係式を
.この関係式を 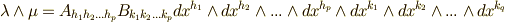 に適用します.
に適用します. 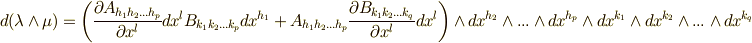
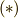 . ここで
. ここで 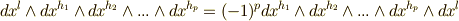 を使うと,式
を使うと,式 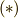 を次式のように変形できます.
を次式のように変形できます. 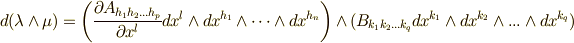
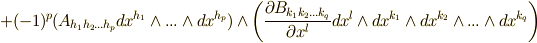 右辺は
右辺は 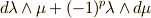 と書けますので定理が示されました.■
と書けますので定理が示されました.■
簡単な場合について,この定理を確認しておきましょう.ただし,  次微分形式(ただの関数)の積に関しては,ウェッジ積ではなく,何も書かないか従来の積のように
次微分形式(ただの関数)の積に関しては,ウェッジ積ではなく,何も書かないか従来の積のように  で書くことにします.
で書くことにします.
【 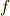 も
も 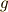 も
も  次微分形式の場合】
次微分形式の場合】

【 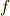 が
が  次微分形式,
次微分形式, 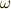 が
が  次微分形式の場合】
次微分形式の場合】
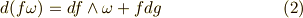

式  は,積の関数の全微分を取るという,高校で習う公式に他なりません.ここでは,式
は,積の関数の全微分を取るという,高校で習う公式に他なりません.ここでは,式  と式
と式 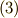 の違いに注意して下さい.
の違いに注意して下さい.
ポアンカレの補題
任意の次数の微分形式に対し,二回外微分を取ったら零になります.(これを,ポアンカレの補題と呼びます.)
theorem
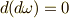
この性質は,三次元ユークリッド代数上の外積代数なら,高々 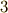 次の微分形式までしか出てきませんし,実際に手計算して確認することができます.一度計算してみると,理解が深まると思います.
次の微分形式までしか出てきませんし,実際に手計算して確認することができます.一度計算してみると,理解が深まると思います.
proof
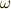 を
を 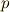 次微分形式とし,
次微分形式とし, 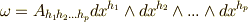 と置きます.
と置きます. 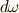 は
は  次微分形式になります.
次微分形式になります.  .添字の名前は任意ですので,若干トリッキーですが,次のような変形を行います.
.添字の名前は任意ですので,若干トリッキーですが,次のような変形を行います. 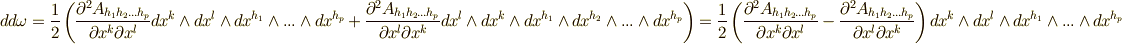 ここで
ここで  の偏導関数が滑らかだとすれば,偏微分の順序を変えることができ,
の偏導関数が滑らかだとすれば,偏微分の順序を変えることができ, 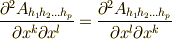 が成り立ちますので
が成り立ちますので 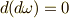 が示されます.■
が示されます.■
この定理の本質的な部分は, 滑らかな関数の二階偏導関数では,偏微分の順序を入れ替えられる という性質に負うています.この定理は,微分形式の計算で非常に重要ですので,しっかり身につけるようにして下さい.
| [*] | ベクトル解析で重要な関係式であった  という関係式( 参考 )は,どちらも実はこのポアンカレの補題の一つの表現に過ぎないことがもうすぐ分かります. という関係式( 参考 )は,どちらも実はこのポアンカレの補題の一つの表現に過ぎないことがもうすぐ分かります. |
ところで,ベクトル解析には, 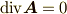 となるベクトル場には
となるベクトル場には  となるベクトルポテンシャルが存在するという定理がありましたが,これは微分形式を使えばより一般的に『
となるベクトルポテンシャルが存在するという定理がありましたが,これは微分形式を使えばより一般的に『 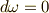 となる
となる 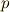 次微分形式には
次微分形式には  となる
となる  次微分形式
次微分形式 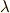 が存在する』と表現することが出来ます.これはポアンカレの補題の変形で,むしろ,こちらの定理をポアンカレの補題と呼ぶことの方が多いと思います.そのうち,きちんと考える予定ですが,証明するには,先に勉強しておかないといけない事柄が多くあります.現段階では,定理の結果だけ示しておきます.
が存在する』と表現することが出来ます.これはポアンカレの補題の変形で,むしろ,こちらの定理をポアンカレの補題と呼ぶことの方が多いと思います.そのうち,きちんと考える予定ですが,証明するには,先に勉強しておかないといけない事柄が多くあります.現段階では,定理の結果だけ示しておきます.
theorem
凸集合で定義された 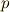 次微分形式
次微分形式 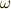 が,
が, 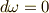 を満たすとき,
を満たすとき, 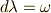 を満たす
を満たす  次微分形式
次微分形式 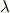 が存在します.
が存在します.
この定理は,多様体の埋め込みという話題を勉強するときにも,また取り上げます.
| [†] |  となる となる 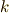 次微分形式を閉形式と呼びます.(閉形式とは,つまり一回外微分を取ったら 次微分形式を閉形式と呼びます.(閉形式とは,つまり一回外微分を取ったら  になる微分形式のことです.)ポアンカレの補題で,『 凸集合で定義された』というような文が気になりますが,実は,微分形式が定義されている空間(多様体)によっては,必ずしも全ての閉形式が になる微分形式のことです.)ポアンカレの補題で,『 凸集合で定義された』というような文が気になりますが,実は,微分形式が定義されている空間(多様体)によっては,必ずしも全ての閉形式が 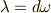 を満たすポテンシャル を満たすポテンシャル 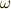 を持つわけではないのです.ややこしくなってきましたね.ポテンシャルを持つ閉形式を,特に完全形式と呼びます.ユークリッド空間に限れば,閉形式は常に完全形式となり, を持つわけではないのです.ややこしくなってきましたね.ポテンシャルを持つ閉形式を,特に完全形式と呼びます.ユークリッド空間に限れば,閉形式は常に完全形式となり,  となる となる 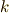 次微分形式 次微分形式 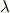 に対し, に対し, 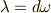 を満たす を満たす 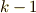 微分形式 微分形式 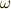 の存在は保証されます.一般の多様体上で定義される微分形式では,多様体の幾何学的性質が効いてきます.今の段階で,あまり難しく考える必要はありませんが,ここでポアンカレの補題の一般的な証明を出来ないというのは,このような事情によるものです.少し,多様体論と位相幾何学の勉強を先にしないといけません. の存在は保証されます.一般の多様体上で定義される微分形式では,多様体の幾何学的性質が効いてきます.今の段階で,あまり難しく考える必要はありませんが,ここでポアンカレの補題の一般的な証明を出来ないというのは,このような事情によるものです.少し,多様体論と位相幾何学の勉強を先にしないといけません. |
練習問題
三次元ユークリッド空間上のベクトル場 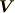 と関数
と関数 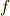 に対して, もう一度grad,div,rot を参考に,以下の二式を示して下さい.(ヒント:
に対して, もう一度grad,div,rot を参考に,以下の二式を示して下さい.(ヒント: 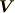 は二次微分形式,
は二次微分形式, 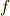 は零次微分形式と考えます.)
は零次微分形式と考えます.)
(1) 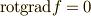
(2) 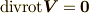
ポアンカレ
ポアンカレ(  )はフランスの東部の町ナンシーに生まれました.ポアンカレの父は大学の医学教授でした.フランスの首相や大統領を歴任したレイモンド・ポアンカレ(
)はフランスの東部の町ナンシーに生まれました.ポアンカレの父は大学の医学教授でした.フランスの首相や大統領を歴任したレイモンド・ポアンカレ(  )は従兄弟に当たります.優秀な家系だったようです.ポアンカレは体が弱く病気がちでしたが,学校では『数学の怪物』の異名を取り,全国の優秀な生徒で競われる数学コンクールで優勝するなど,小さい頃から才能を発揮していました.ポアンカレは黒板がよく見えないほど目が悪かったそうですが,聴覚情報を視覚化する能力に飛びぬけて優れおり,先生の話だけからノートを取っていたということです.この能力は,幾何学の図形把握能力と関係あるに違いありません.大学は,パリ大学でエルミート(
)は従兄弟に当たります.優秀な家系だったようです.ポアンカレは体が弱く病気がちでしたが,学校では『数学の怪物』の異名を取り,全国の優秀な生徒で競われる数学コンクールで優勝するなど,小さい頃から才能を発揮していました.ポアンカレは黒板がよく見えないほど目が悪かったそうですが,聴覚情報を視覚化する能力に飛びぬけて優れおり,先生の話だけからノートを取っていたということです.この能力は,幾何学の図形把握能力と関係あるに違いありません.大学は,パリ大学でエルミート(  )のもとで学び,後にカン大学で数学の教職につきますが,ポアンカレの思考回路は常人とは異なっていたようで,学位論文も大変分かりにくいものだったようですし,生活パターンや講義なども風変わりだったようです.何でも直観的に物事を把握したポアンカレは,必ずしも正確な文を書く人ではなかったようで,彼の論文も非常に読みにくいそうです.
)のもとで学び,後にカン大学で数学の教職につきますが,ポアンカレの思考回路は常人とは異なっていたようで,学位論文も大変分かりにくいものだったようですし,生活パターンや講義なども風変わりだったようです.何でも直観的に物事を把握したポアンカレは,必ずしも正確な文を書く人ではなかったようで,彼の論文も非常に読みにくいそうです.

間違いなく,数学史上きっての天才だろう.
ポアンカレの業績は微分方程式論,位相幾何,群論,保型関数の発見など,数学だけでも非常に広汎な分野に渡っていますが,天体力学における三体問題,流体力学,特殊相対性理論,科学哲学などの分野にも貢献があり,数学者の専門化が進んだ  世紀には珍しい万能型の数学者でした.わずか
世紀には珍しい万能型の数学者でした.わずか 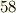 歳で動脈血栓の発作により急死しましたが,
歳で動脈血栓の発作により急死しましたが,  を越す論文と
を越す論文と 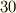 冊以上の著作を残し,また『単連結な三次元閉多様体は三次元球面
冊以上の著作を残し,また『単連結な三次元閉多様体は三次元球面  に同相である』という,ポアンカレ予想として知られる問題は,二十世紀最大の予想問題の一つとして有名です.もっとも,ロシア人数学者グレゴリー・ペレルマン
に同相である』という,ポアンカレ予想として知られる問題は,二十世紀最大の予想問題の一つとして有名です.もっとも,ロシア人数学者グレゴリー・ペレルマン  がその証明に成功した宣言し,その証明も正しいと考えられているようです.(ペレルマンは取材,昇進,賞金,表彰などに一切の関心を示さず,論文もあまり発表せず,フィールズ賞さえ辞退し,母の年金を頼りに故郷で母と二人で暮らし,密かに数学の研究を続けていると言う超変人です.)
がその証明に成功した宣言し,その証明も正しいと考えられているようです.(ペレルマンは取材,昇進,賞金,表彰などに一切の関心を示さず,論文もあまり発表せず,フィールズ賞さえ辞退し,母の年金を頼りに故郷で母と二人で暮らし,密かに数学の研究を続けていると言う超変人です.)