ミンコフスキー空間上の微分形式
この記事では,相対性理論などに使われるミンコフスキー空間という空間上での微分形式を考えてみます.立派な名前がついていますが,どんな空間なのかと言えば,四次元空間です.特徴として,座標基底の中に 計量が負になるものが一つ あります.このような場合, ホッジ作用素 の取り方に注意が必要でした.( ホッジ作用素 や p-ベクトルの内積 の記事中にもミンコフスキー空間に関する注意を書いていますので,参照下さい.)もう一度,ホッジ作用素の定義を思い出しましょう. 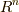 上の
上の 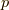 次微分形式の基底を
次微分形式の基底を 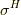 とすると,
とすると, 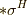 は
は 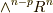 の基底
の基底 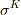 となります.
となります.

ただし, 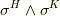 は,ボリュームフォームの基底の偶順列だとします.(これらは全て既習の内容なので,少し説明を端折っています.訳が分からないという人は, ホッジ作用素 の内容をもう一度よく復習して下さい.)式
は,ボリュームフォームの基底の偶順列だとします.(これらは全て既習の内容なので,少し説明を端折っています.訳が分からないという人は, ホッジ作用素 の内容をもう一度よく復習して下さい.)式 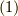 で問題なのは,右辺の
で問題なのは,右辺の 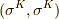 という内積です.ミンコフスキー空間の正規直交基底を
という内積です.ミンコフスキー空間の正規直交基底を 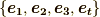 とすると,最初の三つは,普通のユークリッド空間でお馴染みの基底ですが,四番目の
とすると,最初の三つは,普通のユークリッド空間でお馴染みの基底ですが,四番目の 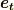 が例の,計量が負になる基底になります.基底の内積は次のようになります.
が例の,計量が負になる基底になります.基底の内積は次のようになります.
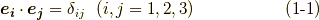
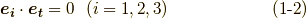

式 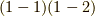 は正規直交基底の定義として,よく知っているものです.式
は正規直交基底の定義として,よく知っているものです.式  が特徴的ですね.このような計量を ローレンツ計量 と呼びます.このため,例えば
が特徴的ですね.このような計量を ローレンツ計量 と呼びます.このため,例えば 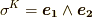 の場合と,
の場合と, 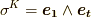 の場合では,内積
の場合では,内積 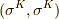 が異なってきます. p-ベクトルの内積 に従って,計算してみましょう.
が異なってきます. p-ベクトルの内積 に従って,計算してみましょう.
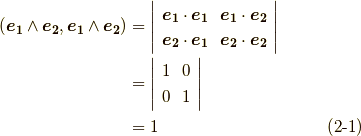
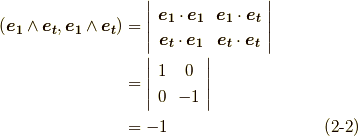
どうやら, 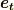 が混ざっていると
が混ざっていると 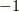 になるようです.以上の議論を念頭に置きつつ,次のセクションではミンコフスキー空間上の微分形式を考えてみます. 四次元の微分形式 とも,後で比べてみて下さい.
になるようです.以上の議論を念頭に置きつつ,次のセクションではミンコフスキー空間上の微分形式を考えてみます. 四次元の微分形式 とも,後で比べてみて下さい.
ミンコフスキー空間上の微分形式
一次微分形式の基底を 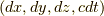 とします.
とします. 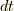 の前についている
の前についている  が妙ですが,これは単なる定数です.気にしないで下さい(・ω・).空間の向きを
が妙ですが,これは単なる定数です.気にしないで下さい(・ω・).空間の向きを 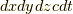 という順列に決めましょう.このとき,ホッジ作用素の写像の仕方に注意が必要です.前セクションの議論により,
という順列に決めましょう.このとき,ホッジ作用素の写像の仕方に注意が必要です.前セクションの議論により, 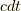 が右辺に出て来る写像には,
が右辺に出て来る写像には, 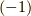 が掛かってきます.
が掛かってきます.
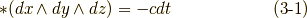
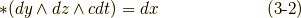
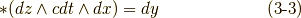
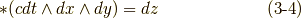
さらに,二次微分形式の基底のホッジ作用素も考えてみましょう.できれば,式 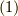 の定義通りに計算して,これらの関係を一度自分で確認してみて下さい.
の定義通りに計算して,これらの関係を一度自分で確認してみて下さい.
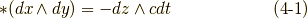
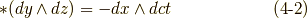
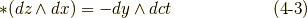
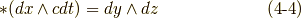
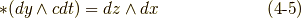
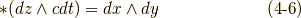
ここで,式 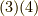 で用いた基底の並びは,全て
で用いた基底の並びは,全て 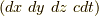 という順列の偶順列になっていますので,右辺に出てきたマイナスは,ひとえに
という順列の偶順列になっていますので,右辺に出てきたマイナスは,ひとえに 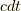 軸の計量が負であるという事情だけによるものです.
軸の計量が負であるという事情だけによるものです. 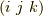 を
を 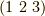 の偶順列とし,
の偶順列とし, 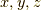 を
を 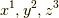 と表現することにすれば,式
と表現することにすれば,式  をまとめて次のように略記することも出来ます.
をまとめて次のように略記することも出来ます.
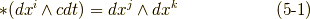
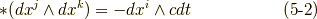
ミンコフスキー空間上の微分形式などという変チクリンなものを考えた理由は,電磁気学の基礎方程式とも言えるマックスウェルの方程式を,微分形式を使って美しく記述したいという動機によるものです.本当に美しく簡単な形にまとまりますので,純粋に美学的・審美的観点からもぜひ眺めてみて欲しいものですし,そのあまりにも単純な形から,(特に幾何学的な考察によって)電磁気学をより深く理解する一助ともなることでしょう.ミンコフスキー空間上の微分形式によるマックスウェル方程式の定式化は, 次 の記事で考えます.
ミンコフスキー
ミンコフスキー空間にその名を残すミンコフスキー(  )は,現在のリトアニア(当時はロシア帝国領)に生まれました.両親はドイツ人で,一家もその後ドイツのケーニヒスベルグ(現在はロシアの飛び地)に引っ越していますので,ミンコフスキーはドイツ人だと考えた方が良さそうです.ミンコフスキーはケーニヒスベルグ大学へ進みますが,数学の才能は抜きん出ていたようです.ヒルベルト(
)は,現在のリトアニア(当時はロシア帝国領)に生まれました.両親はドイツ人で,一家もその後ドイツのケーニヒスベルグ(現在はロシアの飛び地)に引っ越していますので,ミンコフスキーはドイツ人だと考えた方が良さそうです.ミンコフスキーはケーニヒスベルグ大学へ進みますが,数学の才能は抜きん出ていたようです.ヒルベルト(  )は大学の級友で,また新任教官にはフルヴィッツ(
)は大学の級友で,また新任教官にはフルヴィッツ(  )がおり,彼等とは親友とも言える間柄でした.
)がおり,彼等とは親友とも言える間柄でした.
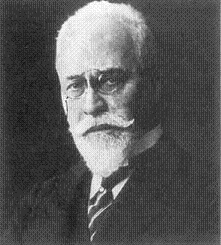
アインシュタインが数学の重要性に目覚めたのは,ミンコフスキーのお陰だ.
後年,ミンコフスキーはボン,ケーニヒスベルグなどで職を得ますが,チューリッヒの  で教鞭を取っていたときの学生にアインシュタイン(
で教鞭を取っていたときの学生にアインシュタイン(  )がいます.最後はヒルベルトの招きに応じてゲッチンゲン大学に落ち着き,数学の研究に没頭します.ミンコフスキーの功績で何よりも有名なものは,ローレンツ(
)がいます.最後はヒルベルトの招きに応じてゲッチンゲン大学に落ち着き,数学の研究に没頭します.ミンコフスキーの功績で何よりも有名なものは,ローレンツ(  )とアインシュタインによる相対性理論を見事に記述する,ミンコフスキー空間という概念を数学的に洗練したことでしょう.ただし,ミンコフスキー自身の興味は純数学的内容に向いており,二次形式や連分数法の研究に時間をかけています.また,「数の幾何学」という分野はミンコフスキーによって創始された,幾何学と整数論が合わさったような分野で,ミンコフスキーの凸型定理という定理は有名です.
)とアインシュタインによる相対性理論を見事に記述する,ミンコフスキー空間という概念を数学的に洗練したことでしょう.ただし,ミンコフスキー自身の興味は純数学的内容に向いており,二次形式や連分数法の研究に時間をかけています.また,「数の幾何学」という分野はミンコフスキーによって創始された,幾何学と整数論が合わさったような分野で,ミンコフスキーの凸型定理という定理は有名です.