微小量の積

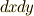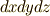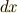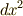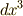面積分や体積分には， dxdy や dxdydz といった量がたくさん出てきます．ここで，少し考えてみましょう．微積分では，いままで微小量の高次の項，例えば $dx^{2}$ や $dx^{3}$ を無視してきました．少し正確に言えば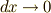， $dx \rightarrow 0$ とした極限では，その影響を無視できると考えて来たわけです．ところが，面積分や体積分には 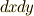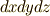dxdy , dxdydz といった形の微小量が出てきました．ここで『あれ，これは二次以上の微小量なんじゃないの？』と引っ掛かった人がいるかも知れません．

この事情は，直観的には次のように理解できます．図で考えれば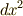， $dx^{2}$ は線素である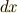を二乗したのに過ぎないのに対し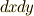， dxdy は微小な面積を表わしているという違いが分かると思います．

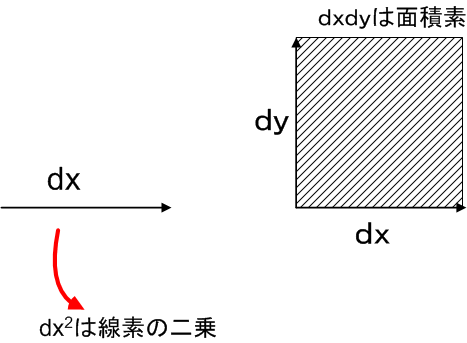
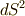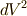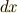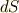体積素についても同様です．『微小量の高次項は落とす』という，微積分学で使っていた近似は有効で， $dS^{2}$ や $dV^{2}$ が式の中に出てきたら落としてしまって構いません．しかし，線素，面積素，体積素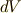は，一口に微小量と言っても 次元が違う微小量 なのです．

Important

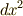$dx^{2}$ は線素という微小量の二次の微小量ですが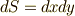， dS=dxdy は面積素という微小量の一次の微小量です．

だいたいの直観的理解は上の図から得られると思いますが，正確な議論は解析学によらなければなりません．

微分形式による表現

微分形式による表現では，線素，面積素，体積素はそれぞれ一次微分形式，二次微分形式，三次微分形式の基底として表現されました．

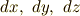
$dx,\ dy, \ dz$

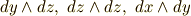
$dy \land dz,\ dz \land dz, \ dx \land dy$

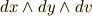
$dx \land dy \land dv$

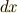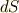前セクションで，『線素，面積素，体積素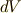は，一口に微小量と言っても次元が違う微小量なのです』と書きましたが，微分形式で書けば，これらは全て異なるベクトル空間の元なのですから，違いはより明快です．

また，『同じ種類の微小量の高次項は落とす』というルールと，微分形式の『同じ元のウェッジ積は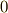になる』という演算則は綺麗に対応しています．（式中，例として 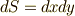dS=dxdy とします．）

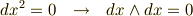
$dx^{2} =0 \ \ \rightarrow \ \ dx \land dx =0$

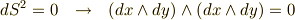
$dS^{2} =0 \ \ \rightarrow \ \ (dx \land dy ) \land (dx \land dy) =0$

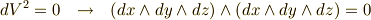
$dV^{2} =0 \ \ \rightarrow \ \ (dx \land dy \land dz) \land (dx \land dy \land dz) =0$

もう一度，強調しておきますが，微分形式の理論は，外積代数の枠組みで，基底を 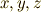x,y,z などの代わりに 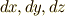dx,dy,dz としてみただけのものでした．そして，外積代数の演算規則そのものは，テンソル代数から導かれたもので，あまり微積分学とは関係なさそうに思えました．ところが，微分形式を，線素，面積素，体積素などと対応させて考えてみると， 微積分の演算法則と外積代数の演算則が，驚くほど整合する ことに気がつくと思います．これは，なぜなんでしょうか？著者も浅学なため，深遠な理由は分かりませんが，とにかく微分形式の表現の美しさには感嘆させられるばかりです．

数学は美しい．驚くほど美しい．美術館に飾れないのが残念だ．

[home] [微分形式] [ページの先頭]