イデアルで外積代数を入れる1
この記事の内容は, イデアルによる類別 の続きになっています.いきなりこのページに来た人は, テンソル の内容,特に テンソル代数 について,それと 代数学 の基礎をそれなりに理解していることが望ましいです.色々,先に勉強しなきゃいけないことがあってごめんなさいm(_ _)m.微分形式の計算だけとりあえず知りたい人は,外積代数をまるまる飛ばして先に行ってしまっても大丈夫です.
テンソル代数から出発
テンソル同士の演算に,テンソル積と呼ばれるものがありました.テンソルには階数という数がありましたが, 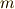 階のテンソルと言えば,
階のテンソルと言えば, 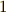 階のテンソル(つまりベクトル)が定義されるベクトル空間
階のテンソル(つまりベクトル)が定義されるベクトル空間 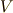 の,
の, 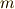 個の直積空間
個の直積空間 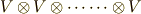 (これもベクトル空間です)の元のことでした.
(これもベクトル空間です)の元のことでした.
さて, 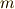 階のテンソルと
階のテンソルと 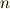 階のテンソルのテンソル積は
階のテンソルのテンソル積は 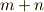 階のテンソルになります.このように,テンソルとテンソルからテンソル積を考えると,幾らでもテンソルの階数が上がっていってしまいますから,『世の中全てのテンソル』を含む空間
階のテンソルになります.このように,テンソルとテンソルからテンソル積を考えると,幾らでもテンソルの階数が上がっていってしまいますから,『世の中全てのテンソル』を含む空間 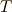 は,
は, 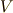 も
も 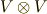 も
も 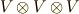 も.....
も..... 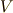 を無限個(!!)つなげた直積空間
を無限個(!!)つなげた直積空間 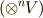 までも,全て含むベクトル空間である必要があります.これを,各ベクトル空間の和として,次のように書きます.
までも,全て含むベクトル空間である必要があります.これを,各ベクトル空間の和として,次のように書きます.
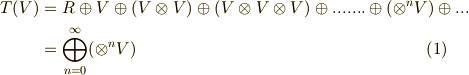
こんな空間を考えたところで,どんなテンソルでも計算できるぞ!という自己満足はあるかも知れませんが,ちょっと大きすぎて使い勝手が悪そうです.
| [*] | 空間を単に大きいとか小さいとか言うのは数学的には不正確ですが,気持ちとして,大きいと言いたい部分を汲んでください (ToT)/~ |
そこで,何とかテンソル空間をもう少し手軽で小さな空間に落としたいのですが,ここで類別という考え方が使えます.
| [†] | 少し違う例ですが,例えば整数は無限にありますが,これを偶数か奇数かに分けてしまえば,たった二つのグループに分けてしまうことができます.当たり前と思うかも知れませんが,よく考えるとすごいことですね.目的に応じて,上手にグループ分けすれば,話をとても簡単にできそうです.これが類別の真髄です.私の部屋と机の上も,類別する必要があります. |
補足:イデアルの復習
次のセクションの議論に備えて,イデアルの性質をちょっと復習しておきます.詳しくは イデアル を参照してください.
【イデアルの性質】
代数 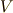 を
を 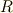 上の環として,そのイデアル
上の環として,そのイデアル 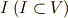 は次の性質を満たします.
は次の性質を満たします.
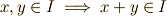 (和)
(和)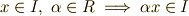 (スカラー積)
(スカラー積)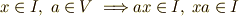 (吸収律)
(吸収律)
吸収律に関しては,右イデアルと左イデアルを分ける方が正確ですが,ここでは両イデアルのみを考えます.両イデアルの場合は,二つをまとめて次のように書くことも出来ます.
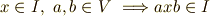
また, 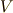 を
を 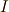 によって類別するとき,
によって類別するとき, 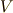 の元
の元 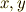 が同じ類に入るとは,次式がなりたつことを言います.
が同じ類に入るとは,次式がなりたつことを言います.
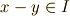
テンソル代数の商代数
前セクションで動機とアイデアをすこし述べましたが,いま, 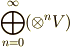 というテンソル代数
というテンソル代数 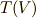 を,何かうまいイデアルで類別して,もう少し扱いやすくしたいのです.どんなイデアルで考えればいいか,という点には色々な候補があると思いますが,結論から先に言ってしまうと元
を,何かうまいイデアルで類別して,もう少し扱いやすくしたいのです.どんなイデアルで考えればいいか,という点には色々な候補があると思いますが,結論から先に言ってしまうと元 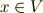 に対して『
に対して『 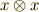 (
( 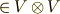 )という元を含む両イデアル』を考えます.
)という元を含む両イデアル』を考えます.
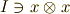
もし,こんなイデアルが存在するなら( 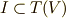 ),イデアルの性質である吸収律から,任意のテンソル
),イデアルの性質である吸収律から,任意のテンソル 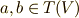 に対して,次のような元も
に対して,次のような元も 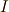 に含まれるはずです.
に含まれるはずです.
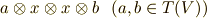
いま, 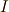 は最低限幾つかの元を含むことが分かったので,
は最低限幾つかの元を含むことが分かったので, 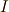 の元を
の元を 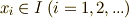 と書きましょう.すると,イデアルの吸収律と和の性質により,一般に次の形で表わされる元も全て
と書きましょう.すると,イデアルの吸収律と和の性質により,一般に次の形で表わされる元も全て  に含まれることが分かります.和は有限和として,
に含まれることが分かります.和は有限和として, 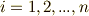 とします.
とします.
| [‡] | ここで和を有限としたのは場当たり的な事情によるものではありません.本当は,イデアルの定義の部分に『和は有限和までとする』と最初に書いておくべきことでした.例えば,いま有理数体のイデアルを考えているとして,もし無限和を取っても良いことにすると 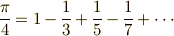 といった無限級数によって無理数である といった無限級数によって無理数である 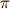 までが表わせてしまいます.これは,もとの有理数体という集合をはみ出しますから困ります.このように,無限和という操作は,一般にもとの代数構造をはみ出す可能性があるため,普通は代数学では別に扱うのです.有限和である限り,幾ら足そうとも,イデアルの元と同士の和はイデアルに入ります. までが表わせてしまいます.これは,もとの有理数体という集合をはみ出しますから困ります.このように,無限和という操作は,一般にもとの代数構造をはみ出す可能性があるため,普通は代数学では別に扱うのです.有限和である限り,幾ら足そうとも,イデアルの元と同士の和はイデアルに入ります. |
これは 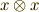 という元を含む最小のイデアルで,『
という元を含む最小のイデアルで,『 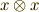 から生成されたイデアル』と呼びます.逆に,式
から生成されたイデアル』と呼びます.逆に,式 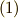 の形の集合が,イデアルの性質を全て満たすことも確認してみて下さい.
の形の集合が,イデアルの性質を全て満たすことも確認してみて下さい.
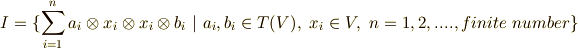
このイデアル 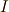 とテンソル代数
とテンソル代数 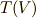 から作った商代数を 外積代数
から作った商代数を 外積代数 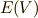 と呼びます.
と呼びます.

もちろん,この外積代数は,最初に 外積代数 で紹介したのと同じものです.ですから,何か特に新しいことがあるわけではありません.(本当に式 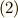 が外積代数になっていることは,次の記事で議論します.まずは一休みしましょう.)外積代数の記事では,外積代数に成り立つ演算規則を天下り的に与え,『とにかく外積代数というものがある』という点から議論をスタートさせていましたから,『どうしてそんなもの考えついたの?』という部分が気持ち悪かった人が,胸のつかえをすっきりさせられれば幸いです.ベクトル解析からずっと勉強してきている人は,次のような流れになっていることが分かるでしょう.ベクトルを主役に,ここまで勉強してきた内容をフローチャートにしてみました.
が外積代数になっていることは,次の記事で議論します.まずは一休みしましょう.)外積代数の記事では,外積代数に成り立つ演算規則を天下り的に与え,『とにかく外積代数というものがある』という点から議論をスタートさせていましたから,『どうしてそんなもの考えついたの?』という部分が気持ち悪かった人が,胸のつかえをすっきりさせられれば幸いです.ベクトル解析からずっと勉強してきている人は,次のような流れになっていることが分かるでしょう.ベクトルを主役に,ここまで勉強してきた内容をフローチャートにしてみました.
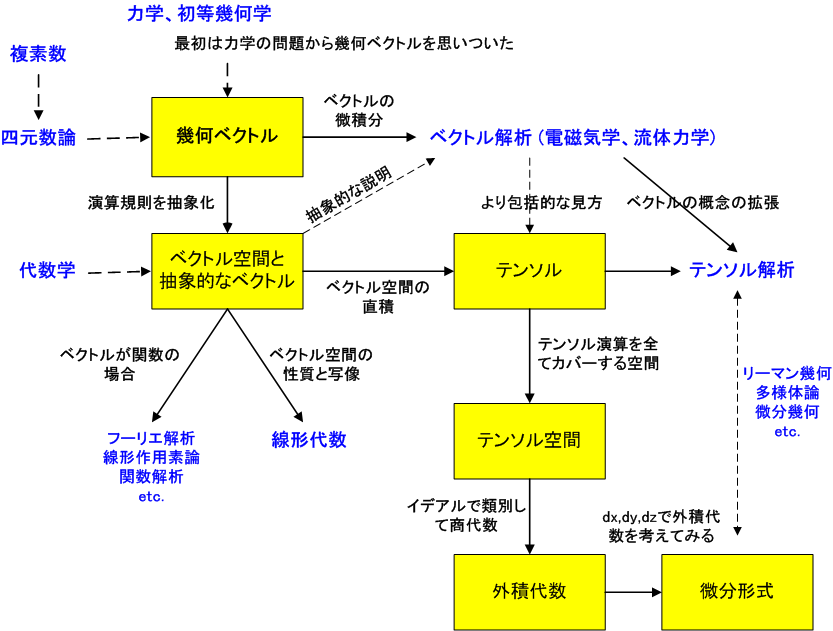
関係しそうな分野は青字で示しました.本当は,もっともっと色々な分野が関係してますし,数学を個別の分野に分けるのはナンセンスですけど,分野を分けておいた方が自習するときに教科書を選びやすいと思ったのです.関連しそうな分野を,ぜひ自分でどんどん勉強してみて下さい.高校で幾何ベクトルを習ってから,ここまでの道のりは結構ありましたね.微分形式まで,あと一息ですよ〜.