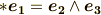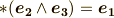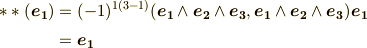ホッジ作用素を使った公式補足
外積代数に関して重要な事柄は,ここまでの記事でほとんどですが, ホッジ作用素 に関する公式だけ,少し補足しておきます.
ホッジ作用素を二回作用させる
以下の議論では,空間の向きを保つとします.(つまり,右手系⇔左手系を途中で入れ替えません.)さて,一般のウェッジ積の次数に関し,  ベクトル
ベクトル 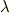 と
と 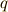 ベクトルのウェッジ積
ベクトルのウェッジ積 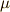 について次の関係がなりたちました.( ウェッジ積について補足 を参照して下さい.)
について次の関係がなりたちました.( ウェッジ積について補足 を参照して下さい.)
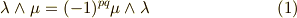
これを基底 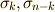 に適用すると次のようになります.ただし,
に適用すると次のようになります.ただし, 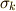 は
は 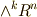 の基底,
の基底, 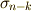 は
は 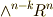 の基底とします.
の基底とします.
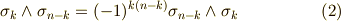
一方,ホッジ作用素の定義式より,次式が言えました.空間の計量が分からないので,右辺の内積はそのままにしておきます.
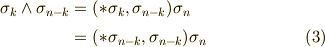
式 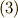 で
で 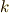 と
と 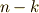 を入れ替えると次式を得ます.
を入れ替えると次式を得ます.
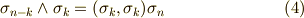
そこで,式 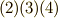 を見比べて,次式が得られます.これは言わば,ホッジ作用素の逆作用を表わす式だと言えます.
を見比べて,次式が得られます.これは言わば,ホッジ作用素の逆作用を表わす式だと言えます.
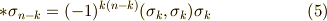
式 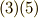 より,ホッジ作用素を二回連続して作用させる場合の表式を得られます.(いま,基底としては正規直交基底を考えていますので,
より,ホッジ作用素を二回連続して作用させる場合の表式を得られます.(いま,基底としては正規直交基底を考えていますので, 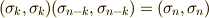 となることに注意して下さい.)
となることに注意して下さい.)
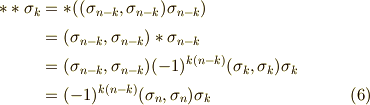
基底の内積 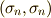 は, p-ベクトルの内積 で定義したように,
は, p-ベクトルの内積 で定義したように,  の基底のうち,計量がマイナスとなる基底の個数に応じて
の基底のうち,計量がマイナスとなる基底の個数に応じて  のどちらかの値を取ります.これで,ホッジ作用素を二連続で作用させた場合の公式が得られました.ボリュームフォームの内積は,
のどちらかの値を取ります.これで,ホッジ作用素を二連続で作用させた場合の公式が得られました.ボリュームフォームの内積は,  の基底で計量を負をするもの(例えばミンコフスキー空間の時間軸)の個数を
の基底で計量を負をするもの(例えばミンコフスキー空間の時間軸)の個数を  として,
として, 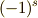 と書けますので,式
と書けますので,式 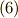 は次のようにまとめられます.(符号定数
は次のようにまとめられます.(符号定数 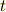 を使って
を使って 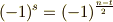 としても同じです.)
としても同じです.)
theorem
一つの定理
ホッジ作用素に関して,もう一つ定理を補足しておきます. 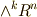 に属する二つの元
に属する二つの元 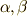 に対し,次式が成り立ちます.
に対し,次式が成り立ちます.
theorem
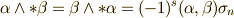
proof
 を
を 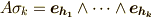 と書くとき,定理の両辺を
と書くとき,定理の両辺を 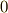 にしないのは,
にしないのは, 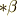 の基底が
の基底が 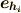 を含まないときだけです.( ホッジ作用素 の記事を参照して下さい.)このことは,裏を返せば
を含まないときだけです.( ホッジ作用素 の記事を参照して下さい.)このことは,裏を返せば 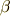 の基底が
の基底が 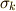 だということです.そこで,
だということです.そこで, 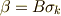 と書きます.
と書きます. 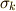 と,構成する基底を重複しない
と,構成する基底を重複しない 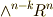 の基底を
の基底を 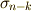 と書きます.このとき,
と書きます.このとき, 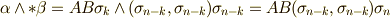 と変形できますが,さらに式
と変形できますが,さらに式  を用いて
を用いて  と変形されます.これで定理が示されました.■
と変形されます.これで定理が示されました.■
参考文献
- 著,『 Differential Forms with Applications to the Physical Science』( Dover Publications Inc., 1990, 032111583x)
 で考えましょう.正規直交基底を
で考えましょう.正規直交基底を  と取り,ボリュームフォームを
と取り,ボリュームフォームを 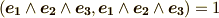 と決めます.このとき,例えば,
と決めます.このとき,例えば, 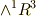 の基底
の基底 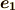 と
と 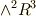 の基底
の基底 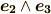 は,ホッジ作用素によって次のように移されるのでした.(
は,ホッジ作用素によって次のように移されるのでした.(