四次元の微分形式

いままでずっと三次元ユークリッド空間上の微分形式ばかり考えていましたが，四次元の微分形式も考えてみます．次の記事 ミンコフスキー空間の微分形式 では，ミンコフスキー空間という，計量が負になるような軸のある四次元空間を考えますが，この記事ではとりあえず，普通の計量を持った四次元ユークリッド空間を考えておきます．復習を兼ねた，ミンコフスキー空間の準備編とも言うべき記事ですので気楽に読んで下さい．

四次元の微分形式

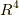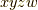すでに，一般の次元の微分形式の定義も 微分形式 で紹介していますので，このセクションの内容は復習になります．いま，実数上の四次元ユークリッド空間 R^{4} に座標系 xyzw を取れるとすると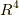， R^{4} 上の外積空間には 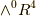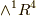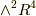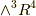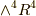\land ^{0}R^{4} , \land ^{1}R^{4} , \land ^{2}R^{4} , \land ^{3}R^{4} , \land ^{4}R^{4} の五種類があり，各空間上の微分形式の基底は次のようになります．

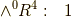
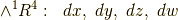
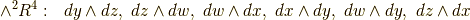
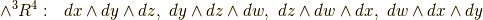
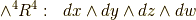
\land ^{0}R^{4}: \ \ 1 \land ^{1}R^{4}: \ \ dx, \ dy, \ dz, \ dw \land ^{2}R^{4}: \ \ dy \land dz, \ dz \land dw, \ dw \land dx, \ dx \land dy, \ dw \land dy , \ dz \land dx \land ^{3}R^{4}: \ \ dx \land dy \land dz, \ dy \land dz \land dw, \ dz \land dw \land dx, \ dw \land dx \land dy \land ^{4}R^{4}: \ \ dx \land dy \land dz \land dw

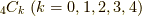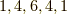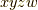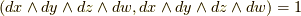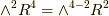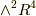各外積空間の次元は，それぞれ， {}_{4}C_{k} \ (k=0,1,2,3,4) に対応して 1,4,6,4,1 となっている点を確認して下さい．もう一つ注意するのは空間の向きです．ボリュームフォームに xyzw の順列に向きをつけて， (dx \land dy \land dz \land dw , dx \land dy \land dz \land dw)=1 とするのは良いでしょう． R^{3} 上の微分形式と異なるのは， \land ^{2}R^{4}=\land ^{4-2}R^{2} のため， \land ^{2}R^{4} の基底のホッジ作用素を取ったものが 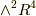\land ^{2}R^{4} の基底自身になるという点です（ 自己双対 ）．この点に注意して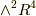， \land ^{2}R^{4} の基底のうち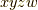， xyzw の偶順列 yzxw , yxwz , ywzx , xzwy , xwyz , zwxy , zxyw , zywx , wxyz , wyzx , wzxy 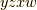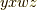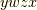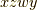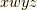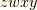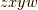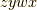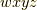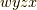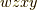から，前半の二つと後半の二つをそれぞれ並べた形のものを正と決めます．（自分でも計算して確認してみて下さいね．）

何か引っ掛かった点がある人は，次の記事に進むまえに曖昧な部分を復習しておいて下さい．