ウェッジ積の座標変換
実数上の  次元ベクトル空間
次元ベクトル空間  の一つの基底を
の一つの基底を 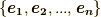 とし,これと異なる基底
とし,これと異なる基底 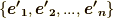 への座標変換
への座標変換 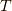 を考えます.
を考えます.
| [*] | いままで,ベクトル空間の記号に 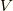 を多く使ってきましたが,今後,実数上という意味と次元を強調して を多く使ってきましたが,今後,実数上という意味と次元を強調して  と書くようにします.ユークリッド空間 と書くようにします.ユークリッド空間  もミンコフスキー空間 もミンコフスキー空間  も実数上のベクトル空間ですので,まとめて も実数上のベクトル空間ですので,まとめて  と書けます.特に区別する場合には, と書けます.特に区別する場合には,  とか とか  と書くことにします. と書くことにします. |

この変換 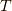 の表現行列を
の表現行列を ![A=[a_{i}^{j}]](./1b508abdffa58518758248a8802207a5.png) とします.この行列を使うと,式
とします.この行列を使うと,式 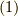 は
は 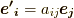 と表わされますので,例えば二階のウェッジ積の座標変換は次のようになります.
と表わされますので,例えば二階のウェッジ積の座標変換は次のようになります.
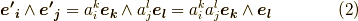
右辺は縮約によって和になっていますから,実際に展開して全部の項を書き出すのは大変です.しかし,原理としては,普通のベクトル空間  の座標変換式をウェッジ積の関係式に代入するだけです.似たような計算はテンソル代数で何度も見てますから,何も難しいことは無いと思います.
の座標変換式をウェッジ積の関係式に代入するだけです.似たような計算はテンソル代数で何度も見てますから,何も難しいことは無いと思います.
∧nの基底の変換
特に 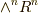 の基底(最高次数の外積空間)
の基底(最高次数の外積空間) 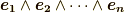 の座標変換を考えてみましょう.
の座標変換を考えてみましょう. 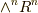 は一次元空間ですから(
は一次元空間ですから( 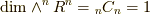 ),基底の写像にはスカラー倍しかありません.では,そのスカラーはどのような値なのかと言うと,
),基底の写像にはスカラー倍しかありません.では,そのスカラーはどのような値なのかと言うと, 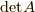 になるのです.これは大変にシンプルな結果です.
になるのです.これは大変にシンプルな結果です.
theorem
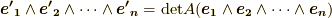
proof
定義通りに座標変換をすると 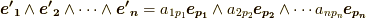 と書けますが
と書けますが 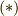 ,右辺は更に行列成分を外に出して
,右辺は更に行列成分を外に出して 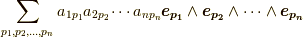 と変形できます.ここで,もし
と変形できます.ここで,もし 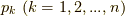 の中に同じ数字が二回出てくれば,ウェッジ積の性質よりその項は
の中に同じ数字が二回出てくれば,ウェッジ積の性質よりその項は 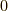 になりますので,
になりますので, 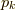 は全て異なる数字であり,結局,
は全て異なる数字であり,結局,  は,
は, 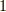 から
から  の数字の異なる順列について総和を取るという意味になります.
の数字の異なる順列について総和を取るという意味になります. 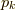 の順列を
の順列を  と書くことにすると,
と書くことにすると, 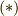 式右辺は
式右辺は 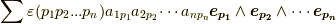 となりますが,これは 行列式の定義 より,
となりますが,これは 行列式の定義 より, 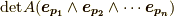 と書けます.■
と書けます.■
この結果は『空間の向き』を考えるときに特に重要になります.例えば三次元で 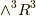 を考えると,基底には
を考えると,基底には  の形のもの一つしかありません.いま
の形のもの一つしかありません.いま  を正規直交基底だとし,長さを変えないように座標変換として直交変換だけを考えるとしても,直交行列の行列式には
を正規直交基底だとし,長さを変えないように座標変換として直交変換だけを考えるとしても,直交行列の行列式には 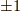 の二つがあります.つまり,上の定理により,座標変換後の基底は
の二つがあります.つまり,上の定理により,座標変換後の基底は 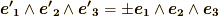 と表わされるということです.
と表わされるということです.
これだけでは,まだ何が重要なのか分かり難いかも知れません.では,少し先走って,微分形式の話まで触れましょう.微分形式の理論の中では,外積空間の基底として,積分計算に出てきた微小量 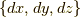 を考えますが,
を考えますが, 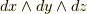 は,今まで体積素として体積分のときに考えていた
は,今まで体積素として体積分のときに考えていた 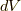 に相当する量になります.これを先ほどの座標変換式にそのまま宛てはめれば,
に相当する量になります.これを先ほどの座標変換式にそのまま宛てはめれば,  という意味に解釈できますね.体積の符号が変わる??これを見て,ムムゥと思って欲しいところです.これと似た話が ベクトル三重積 にありました.ベクトルの張る平行六面体の体積の符号が,右手系⇔左手系を入れ替えたときに変わるという話でした.まさに,先ほどの公式は ベクトル三重積の符号と右手系⇔左手系の符号を説明するもの になっているのです.とは言うものの,まだ多くの読者の方にとっては,旧来のベクトル解析(特にベクトルの積分)に,外積代数の理論をどう使えるのか,その辺りの関係がまだ明快ではないと思います.詳しくは,微分形式の理論でベクトルの積分定理を考え直す中で整理して行く予定ですので,焦らずゆっくり進みましょう.
という意味に解釈できますね.体積の符号が変わる??これを見て,ムムゥと思って欲しいところです.これと似た話が ベクトル三重積 にありました.ベクトルの張る平行六面体の体積の符号が,右手系⇔左手系を入れ替えたときに変わるという話でした.まさに,先ほどの公式は ベクトル三重積の符号と右手系⇔左手系の符号を説明するもの になっているのです.とは言うものの,まだ多くの読者の方にとっては,旧来のベクトル解析(特にベクトルの積分)に,外積代数の理論をどう使えるのか,その辺りの関係がまだ明快ではないと思います.詳しくは,微分形式の理論でベクトルの積分定理を考え直す中で整理して行く予定ですので,焦らずゆっくり進みましょう.