ウェッジ積について補足
まず,  次元のベクトル空間を
次元のベクトル空間を 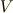 とします.私達は,
とします.私達は, 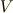 とウェッジ積によって,外積空間
とウェッジ積によって,外積空間 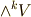 を生成しました.
を生成しました. 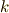 階の外積空間の次元は
階の外積空間の次元は 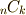 で,
で, 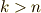 では
では 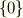 となってしまいます.この記事では, 外積代数 の記事で導入したウェッジ積という演算について,もう少し考察を深めてみます.
となってしまいます.この記事では, 外積代数 の記事で導入したウェッジ積という演算について,もう少し考察を深めてみます.
p-ベクトル
いま,外積空間 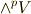 の基底は,
の基底は, 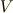 の基底を
の基底を  として,
として, 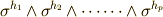 の形で表わされます.(ただし,ここで
の形で表わされます.(ただし,ここで  とします.)よって,
とします.)よって,  に含まれる任意の元は,こうした基底の一次結合の形で表わされるはずです.
に含まれる任意の元は,こうした基底の一次結合の形で表わされるはずです.
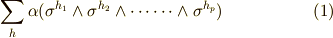
このように,外積空間 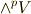 に含まれる元を,外積空間の次数を冠して p-ベクトル のように呼ぶことにします.(具体的には
に含まれる元を,外積空間の次数を冠して p-ベクトル のように呼ぶことにします.(具体的には  ベクトル,
ベクトル,  ベクトルなどのように呼びます.)
ベクトルなどのように呼びます.)
ウェッジ積の代数的性質:補足
ウェッジ積の代数的性質については,既に 外積代数 で次の四つに触れました.
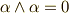
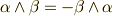 (交代性)
(交代性)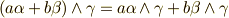 (分配則)
(分配則)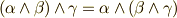 (結合則)
(結合則)
さらに,次の性質を追加しておきます.
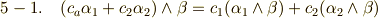
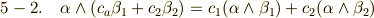
五番目の性質は 双線形性 です.
| [*] | 結合則に関して,ベクトルの外積  には結合則が成り立たないことをもう一度思い出してください.ベクトルの外積はウェッジ積よりもだいぶ厳しい条件の演算です.また, 外積代数 の最後の註に少し書いたことですが,ウェッジ積はテンソル積に交代性を付け加えた演算だと見ることが出来ます.テンソルは一般的に多重線形性を持つのでしたから,このような立場から見れば,ウェッジ積が双線形性を持つのも納得のいくことです. には結合則が成り立たないことをもう一度思い出してください.ベクトルの外積はウェッジ積よりもだいぶ厳しい条件の演算です.また, 外積代数 の最後の註に少し書いたことですが,ウェッジ積はテンソル積に交代性を付け加えた演算だと見ることが出来ます.テンソルは一般的に多重線形性を持つのでしたから,このような立場から見れば,ウェッジ積が双線形性を持つのも納得のいくことです. |
高次のウェッジ積
外積空間 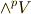 と
と 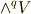 (ただし
(ただし 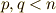 )を考えます.
)を考えます. 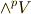 の元と
の元と 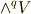 の元のウェッジ積は,一般に
の元のウェッジ積は,一般に 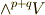 の元になると考えられますので,外積
の元になると考えられますので,外積  による二項演算は次のような写像を意味すると考えられます.
による二項演算は次のような写像を意味すると考えられます.
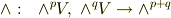
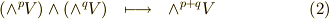
これはp-ベクトルとq-ベクトルのウェッジ積が(p+q)-ベクトルになるという意味です.ただし, 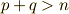 のとき,(p+q)-ベクトルは
のとき,(p+q)-ベクトルは 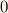 だと決めます.このとき,
だと決めます.このとき,  ベクトル
ベクトル 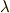 と
と 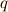 ベクトルのウェッジ積
ベクトルのウェッジ積 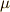 について次の性質がなりたちます.
について次の性質がなりたちます.
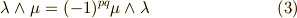
ウェッジ積の交代性より 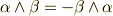 が言えたわけですが,
が言えたわけですが, 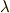 の基底(
の基底( 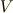 の元を
の元を 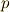 個ウェッジ積で結合したもの)と
個ウェッジ積で結合したもの)と 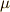 の基底(
の基底( 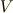 の元を
の元を 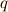 個ウェッジ積で結合したもの)を,隣同士の元を交換する操作を何度も行うことで入れ替えるとき( 外積代数 の記事中でも同じ操作をしましたね),何回入れ替える必要があるかという話です.証明はしませんが,簡単なので自分で考えてみて下さい.(ヒント:数学的帰納法を使えば簡単に示せます.)
個ウェッジ積で結合したもの)を,隣同士の元を交換する操作を何度も行うことで入れ替えるとき( 外積代数 の記事中でも同じ操作をしましたね),何回入れ替える必要があるかという話です.証明はしませんが,簡単なので自分で考えてみて下さい.(ヒント:数学的帰納法を使えば簡単に示せます.)
反対称的な書き方
まずベクトル空間 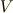 から生成した外積空間
から生成した外積空間 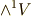 を考え,1-ベクトル
を考え,1-ベクトル 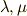 を取ります.
を取ります. 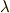 と
と 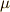 はそれぞれ,
はそれぞれ, 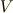 の基底
の基底 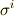 を使って次のように書けるはずです.
を使って次のように書けるはずです.


ここで 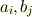 はスカラーの共変成分です.後の都合により,式
はスカラーの共変成分です.後の都合により,式 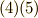 の右辺では縮約をわざと使いませんでした.では,さっそく
の右辺では縮約をわざと使いませんでした.では,さっそく 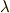 と
と 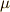 のウェッジ積を取ってみましょう.
のウェッジ積を取ってみましょう.
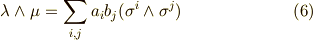
ウェッジ積の表現自体はこれで合っていますが,項数をもう少し節約して書くことができます.基底の性質 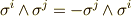 を使うと, 総和を半分に減らすことができるでしょう.
を使うと, 総和を半分に減らすことができるでしょう.
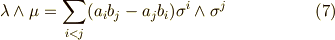
なんだか,お馴染みのベクトルの外積にそっくりな形が出て気ました.式 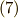 のような書き方が絶対必要という訳ではありませんが,教科書によっては,こんな表記をいきなり使っているものもありますので,見てもびっくりしないで下さい.
のような書き方が絶対必要という訳ではありませんが,教科書によっては,こんな表記をいきなり使っているものもありますので,見てもびっくりしないで下さい.
ウェッジ積の例
計算練習のつもりで,次の左辺を展開して,自分で右辺を導いて下さい. 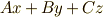 などは,1-ベクトルで,
などは,1-ベクトルで, 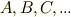 は係数,
は係数, 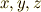 を基底とします.
を基底とします.
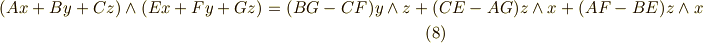
もう一つ,1-ベクトルと2-ベクトルのウェッジ積も計算してみて下さい.
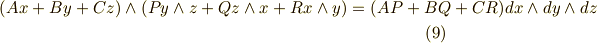
左辺からちゃんと右辺が導けましたか?これがスラスラできれば,ウェッジ積はもう大丈夫です.実は,この二式はベクトルの外積と内積の計算に対応する形になっています.(よく眺めて見てください.)ただし,ウェッジ積はベクトルの外積よりも一般的な演算ですので,このままいきなりウェッジ積をベクトルの演算に関連付けることは出来ません.まずホッジ作用素というものを考える必要があります.その話は,また稿を改めて書きたいと思います.
| [†] | 以前 もう一度だけ内積・外積 の記事中に,ベクトルのテンソル積に『ルールを導入する』ことによって,内積や外積を括り出してくる,というような内容を書きました.二階のテンソルを紹介する目的の記事でしたので,『ルールって何なんだ?』『どうやってルールを入れるんだ?』という点には触れませんでした.だんだん,そのルールがウェッジ積の演算規則であったことが分かってくると思います.また,テンソル代数にどうやってルールを入れたら外積代数になるのか,という点ですが,実は代数学で勉強したイデアル,類別,商集合といった概念を使います.少しマニアックな内容になりますが, イデアルで外積代数を入れる で取り上げる予定です. |