ストークスの定理再々考

ここまでに，ベクトル解析で勉強した 平面のグリーンの定理 ， ガウスの発散定理 ， ストークスの定理 が，微分形式を使えば全て次の形に表現できることを確認してきました．

\int \limits _{D} \partial \omega = \int \limits _{\partial D} \omega \tag{1}

特に，グリーンの定理は，ストークスの定理の領域が『二次元につぶれた特別な場合』とも言えます．（ベクトル解析分野の 平面のグリーンの定理 ， ストークスの定理 でも，このことについて触れました．）実は，平面のグリーンの定理を出発点として，ストークスの定理を示すことが出来ます．途中で使う考え方は，すでに個別に証明済みなので，全体の思考の流れだけを図で示します．まずスクロールダウンして，図は下から上へ見て行って下さい．（説明は，図の下に続けます．）

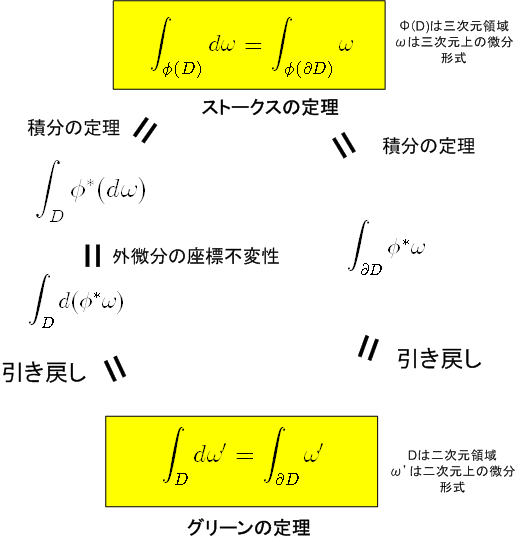
Joh-StokesProof.gif

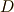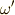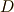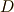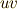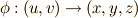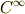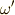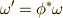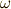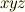まず，二次元領域 D 上で定義される一次微分形式 \omega ' があり， D 上で，平面のグリーンの定理がなりたっているとします． D に取れる座標を，例えば uv 座標系としましょう．このとき， \phi : (u,v) \rightarrow (x,y,z) という C^{\infty} 級写像を考え， \omega ' に対しては \omega ' = \phi ^{*} \omega という引き戻しを考えます． \omega は， xyz 座標系を取れる三次元領域で定義される微分形式です．左辺は， 外微分の座標不変性 を使って 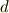d の順序を入れ替え，最後は 微分形式と積分の向き で証明した定理を使って，ストークスの定理にまで変形します．いままでに，勉強した知識の総動員という観がありますね．

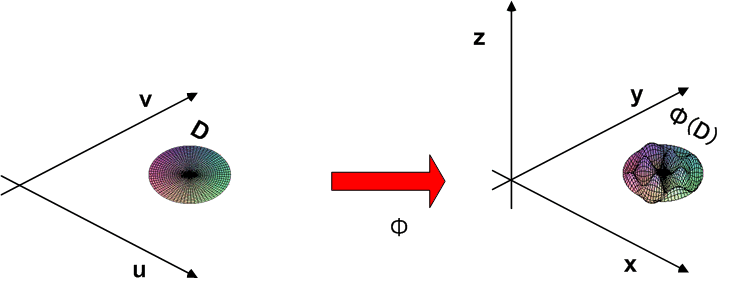
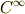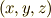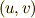大事な点は，引き戻しによって，平面のグリーンの定理が，三次元のストークスの定理にまで 膨らまされている ことです．これは， C^{\infty} 級の連続な一対一写像によって， (x,y,z) を (u,v) で表現できたからなのですが，次元が変わっても良いという引き戻しの性質により( 微分形式の引き戻し１ 最後の註参照)，定理を拡張できたという点が何と言っても感動的です．

Joh-Pullback99.gif

ボコッという効果音もぜひ入れたい．

非常にいい加減ではありましたが，取り敢えず，この記事では平面のグリーンの定理をストークスの定理へ拡張できることを示しました．引き戻しという操作にも，具体的なイメージが湧いたのではないでしょうか．もっとも，平面のグリーンの定理とストークスの定理が同一のものであることは分かりましたが， ガウスの発散定理は，まだ統一されていません ．容易に予想されるように，ガウスの発散定理も，ストークスの定理と同一の（より一般的な）定理の一表現に過ぎないことが分かるのですが，このことは，空間の概念を拡張した概念である， 多様体 を勉強したあとで，より一般的な定理としてまとめて示します．この定理の証明を次の目標として，もう少し頑張りましょう．