マックスウェル方程式への応用
電磁気学の基礎方程式とも言えるのが, マックスウェルの方程式 です.色々な表現がありますが,次の四つのベクトル方程式の形が有名だと思います.



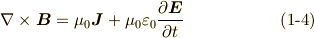
ここで, 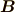 は磁束密度,
は磁束密度, 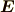 は電場 ,
は電場 , 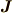 は電流密度,
は電流密度, 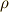 は電荷密度,
は電荷密度, 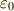 は真空中の誘電率,
は真空中の誘電率, 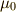 は真空中の透磁率とします.電束密度
は真空中の透磁率とします.電束密度 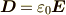 と磁場
と磁場 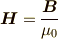 を使って,式
を使って,式  は次のように書くこともあります.
は次のように書くこともあります.

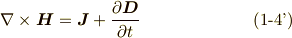
また,式 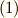 から波動方程式
から波動方程式 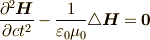 を得ますが,この解は,速度
を得ますが,この解は,速度 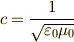 で移動する波を与えます.この
で移動する波を与えます.この  は光速(つまり光は電磁波です)なのですが,この記事では,電磁気学の内容には深入りせず,専らマックスウェルの方程式を微分形式で表わすことだけ考えます.そういうわけで,電磁気学を全然知らなくても,大丈夫です.簡単のため,式
は光速(つまり光は電磁波です)なのですが,この記事では,電磁気学の内容には深入りせず,専らマックスウェルの方程式を微分形式で表わすことだけ考えます.そういうわけで,電磁気学を全然知らなくても,大丈夫です.簡単のため,式 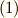 を次の形で書くことにします.
を次の形で書くことにします.




| [*] | 極端な話,この記事を読むだけなら,上に出てきたさまざまな物理量の意味がまったく分かっていなくても大丈夫です.電磁気学は奥が深い分野で,マックスウェルの方程式はその頂点にありますから,生半可な説明は出来ません.マックスウェル方程式から導かれる『光速度はどこから観測しても一定である』という結果から,後に相対性理論が生まれたという道筋もよく知られたものです. |
| [†] | 式  は国際単位系( は国際単位系( 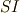 系)に単位を揃えたときの表現として適切です.式 系)に単位を揃えたときの表現として適切です.式 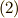 は物理的に言えば は物理的に言えば 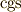 単位系での表現に対応するもので,あまり電磁気学の文脈では流行らない表現かも知れません. 単位系での表現に対応するもので,あまり電磁気学の文脈では流行らない表現かも知れません. 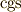 単位系は根絶すべきだというお考えの方もいらっしゃると思いますが,ここは数学の記事だと思って,大目に見てください.m(_ _)m.数学者がマックスウェルの方程式を考えるときは,単位や係数を気にせず,往々にして 単位系は根絶すべきだというお考えの方もいらっしゃると思いますが,ここは数学の記事だと思って,大目に見てください.m(_ _)m.数学者がマックスウェルの方程式を考えるときは,単位や係数を気にせず,往々にして 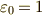 , , 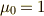 としてしまいます.そうする方が,方程式の対称性(双対性)がよく見えるからです.詳しいことは, 電磁気学 で勉強して下さい. としてしまいます.そうする方が,方程式の対称性(双対性)がよく見えるからです.詳しいことは, 電磁気学 で勉強して下さい. |
三次元ユークリッド空間上の微分形式
最初に,微分形式の復習も兼ねて,三次元ユークリッド空間上で次のような一次微分形式  と二次微分形式
と二次微分形式  を考えてみます.
を考えてみます.



このように定義することが適当である理由は, 微分形式の物理的イメージ (リンク先最後の表)を参考に,各変数の物理的意味を考えてみてください.また,電荷密度  は,零次微分形式(スカラー)ではなく,三次微分形式(擬スカラー)で表される量であると考えるのが適当です.
は,零次微分形式(スカラー)ではなく,三次微分形式(擬スカラー)で表される量であると考えるのが適当です.
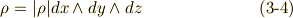
これらを使うと,式 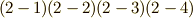 の各式は次のように表現できるでしょう.ただし,時間微分
の各式は次のように表現できるでしょう.ただし,時間微分 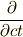 はドット(点)で表わすことにします.
はドット(点)で表わすことにします.




確かに,微分形式を使ってマックスウェルの方程式を表現することは出来ましたが,特にこのように書く旨味はあまり感じられませんね.三次元ユークリッド空間上で考えている限り,マックスウェルの方程式はこれ以上は簡単になりません.しかし, 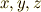 と
と 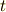 を一緒にして, ミンコフスキー空間 上で考えることで,驚くほど美しく,簡単な表現に帰着します.次セクション以降で,そのことを見ていきます.
を一緒にして, ミンコフスキー空間 上で考えることで,驚くほど美しく,簡単な表現に帰着します.次セクション以降で,そのことを見ていきます.
ミンコフスキー空間で表現してみる
まず,次のような微分形式 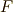 を考えます.これは,ミンコフスキー空間上の二次微分形式です.(おいおい見ていくように,マックスウェルの方程式は,ミンコフスキー空間上で,本当に綺麗に表現されます.)
を考えます.これは,ミンコフスキー空間上の二次微分形式です.(おいおい見ていくように,マックスウェルの方程式は,ミンコフスキー空間上で,本当に綺麗に表現されます.)
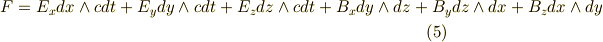
この外微分は,次式のようになります.ここは,丁寧に途中計算も全部示すことにします.
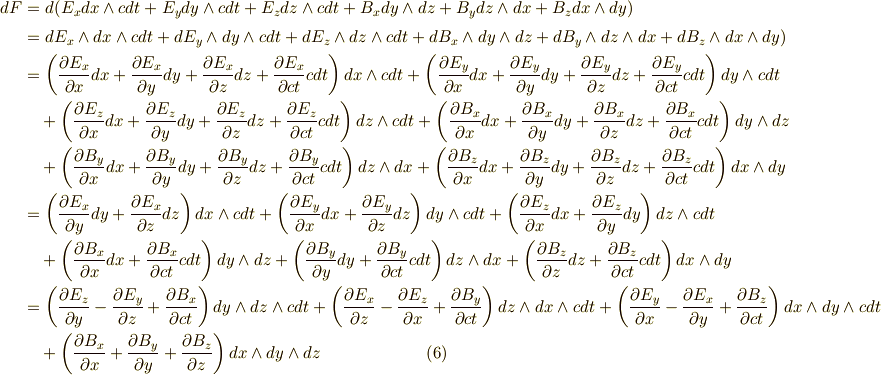
ここで 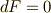 となるのはどんな場合かと考えてみれば,各基底は独立ですから,式
となるのはどんな場合かと考えてみれば,各基底は独立ですから,式 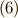 の各成分がそれぞれ
の各成分がそれぞれ 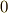 になる場合だと言えます.
になる場合だと言えます.
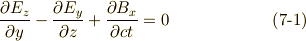
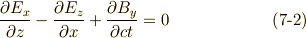
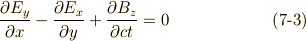
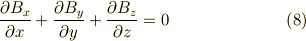
式 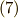 は,ベクトル形ではまとめて
は,ベクトル形ではまとめて 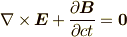 と書けるでしょう.式
と書けるでしょう.式 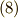 も,ベクトル形で
も,ベクトル形で 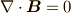 と書けます.これはマックスウェルの方程式
と書けます.これはマックスウェルの方程式 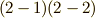 に他なりません.つまり,ミンコフスキー空間上の微分形式を使えば,マックスウェルの方程式
に他なりません.つまり,ミンコフスキー空間上の微分形式を使えば,マックスウェルの方程式 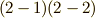 がまとめて次のように表現できるということです.
がまとめて次のように表現できるということです.

美しい!
真空中でのマックスウェルの方程式
今度は,特に真空(自由空間)中でのマックスウェルの方程式を考えます.真空中では, 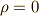 ,
, 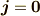 となります.
となります.
【真空(自由空間)におけるマックスウェルの方程式】




残りの二本も微分形式で表現することを考えます.(式 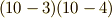 は,いかにも式
は,いかにも式  と対称な形をしていますから,何となく察しはつきますね.)まず,
と対称な形をしていますから,何となく察しはつきますね.)まず, 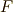 に ホッジ作用素 を作用させた形を考えます.ホッジ作用素の取り方は, ミンコフスキー空間の微分形式 を参考にして下さい.
に ホッジ作用素 を作用させた形を考えます.ホッジ作用素の取り方は, ミンコフスキー空間の微分形式 を参考にして下さい.
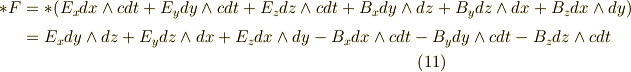
先ほどと同様に, 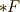 の外微分を取ります.少し,計算は簡単に書きます.
の外微分を取ります.少し,計算は簡単に書きます.
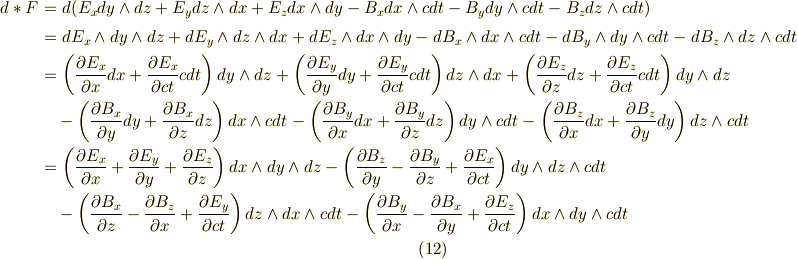
式 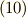 の成分をよく見れば,先ほどと同様,
の成分をよく見れば,先ほどと同様, 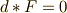 という条件(つまり式
という条件(つまり式 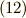 最後の段の,各括弧が
最後の段の,各括弧が 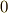 になる)と,マックスウェルの方程式の残りの二本とが等しいことが分かります.
になる)と,マックスウェルの方程式の残りの二本とが等しいことが分かります.


つまり,真空中でのマックスウェル方程式は, 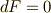 と
と 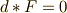 という,極めて簡素な形にまとめることが出来ることが分かりました.
という,極めて簡素な形にまとめることが出来ることが分かりました.
theorem
真空中(自由空間中)でのマックスウェルの方程式は,微分形式を使えば 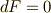 ,
, 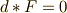 という二本の式に集約できます.
という二本の式に集約できます.
ここまで美しい形にまとめられたのも,まさに微分形式の威力です.
| [‡] | 微分形式の外微分が座標系の取り方によらない,という性質より,微分形式で書いてみれば,マックスウェルの方程式は座標系によらない普遍的な意味を表わす式だということが明快に示されます.また,二本ずつまとめて表現することが出来たわけですが, 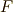 と と 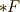 が双対であることを考えれば,見事に対称な双対関係によって表現されたことがよく分かります.ここまで単純な関係式は,特殊な電気現象を記述しているというよりも,なにか非常に本質的な,この世界の構造そのものを記述しているようにも思えます.このような視点で,ミンコフスキー多様体上の位相幾何学的な意味にもっと興味がある人は,例えば こちら を参考にして下さい.もはや,電場とか磁場とかいう物理的な意味はよく分からない幾何学的世界ですが,とても興味深いです. が双対であることを考えれば,見事に対称な双対関係によって表現されたことがよく分かります.ここまで単純な関係式は,特殊な電気現象を記述しているというよりも,なにか非常に本質的な,この世界の構造そのものを記述しているようにも思えます.このような視点で,ミンコフスキー多様体上の位相幾何学的な意味にもっと興味がある人は,例えば こちら を参考にして下さい.もはや,電場とか磁場とかいう物理的な意味はよく分からない幾何学的世界ですが,とても興味深いです. |
| [§] | マックスウェル方程式がこのように美しくまとまったのも,三次元ユークリッド空間ではなく,ミンコフスキー空間で考えてみたからです.そもそも,空間と時間という,感覚的には全然異なる軸を一緒にしたとき,その基底の間にどのような計量が入るのか,という問題は自明ではありません.(計量の定義が変われば,ホッジ作用素の作用も変わってくるはずですよね.)そういう観点からは,本当に素晴らしいアイデアは ローレンツ計量 です.アイデアというか,『この世界はそうなってるんだ』と言われたら実も蓋もないのですが.しかし,この記述の美しさは秀逸です. |
発展・一つにまとめてしまう
式  の右辺ですが,
の右辺ですが, 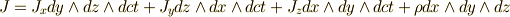 という三次微分形式を考えれば,話を真空中に限らなくても,式
という三次微分形式を考えれば,話を真空中に限らなくても,式  を次の形にまとめることが出来ます.
を次の形にまとめることが出来ます.

式  も再掲しておきます.
も再掲しておきます.


| [¶] | こうすると 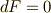 との双対性が崩れてしまいますが, との双対性が崩れてしまいますが, 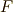 の方にも電荷に相当する磁荷というものを想定すれば,形の上では式 の方にも電荷に相当する磁荷というものを想定すれば,形の上では式 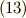 の形で双対な方程式系を作ることは出来ます.ただし,単磁荷(つまり の形で双対な方程式系を作ることは出来ます.ただし,単磁荷(つまり 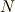 極だけ,もしくは 極だけ,もしくは  極だけ作る磁荷)は存在しないと言われており,そのような形は(多分)物理的にあまり意味がありません. 極だけ作る磁荷)は存在しないと言われており,そのような形は(多分)物理的にあまり意味がありません. |
| [#] | 蛇足ですが,式 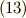 の両辺の外微分をとって得られる関係式 の両辺の外微分をとって得られる関係式 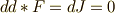 は,電荷・電流の保存則 は,電荷・電流の保存則  の微分形式による表現になっています.確認してみて下さい. の微分形式による表現になっています.確認してみて下さい. |
さて,マックスウェルの最初の二本(つまり 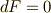 )ですが, ポアンカレの補題 で示した定理(証明はしていませんが)によれば, 『
)ですが, ポアンカレの補題 で示した定理(証明はしていませんが)によれば, 『 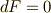 を満たす微分形式には,必ず
を満たす微分形式には,必ず 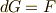 を満たす微分形式
を満たす微分形式 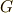 が存在する』ということでした.つまり,
が存在する』ということでした.つまり, 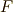 に対し,ポテンシャル
に対し,ポテンシャル 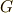 の存在が保証されているわけです.
の存在が保証されているわけです. 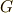 を次の形に置いてみます.
を次の形に置いてみます.
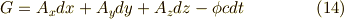
このとき  は次式で与えられます.
は次式で与えられます.

式 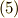 と比べてみて下さい.
と比べてみて下さい.
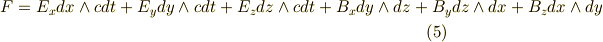
各成分を比較し,  ,
,  と定義すれば,
と定義すれば, 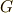 は確かに
は確かに 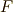 のポテンシャルになっていると言えそうです.(これらの物理的意味については,例えば 電磁ポテンシャル を参考にして下さい.)
のポテンシャルになっていると言えそうです.(これらの物理的意味については,例えば 電磁ポテンシャル を参考にして下さい.)

またしても,これ以上ないほど美しい表現が得られました.さて,任意の微分形式に対し,外微分を二回取れば必ず 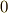 になりますので( ポアンカレの補題 参照),
になりますので( ポアンカレの補題 参照), 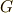 を基準に考えれば,式
を基準に考えれば,式 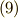 は自動的に満たされて当然です.そこで,最終的に,マックスウェルの方程式は
は自動的に満たされて当然です.そこで,最終的に,マックスウェルの方程式は 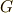 を使った式
を使った式 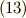 の表現一本にまとめることが出来ます.
の表現一本にまとめることが出来ます.
theorem
【マックスウェルの方程式】 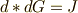
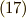
ついに,一本の式になってしまいました.
さらに発展
これ以上簡単にはなりそうもありませんが, ダランベールの作用素 と呼ばれる,次のような演算子を導入してマックスウェルの方程式を記述する方法もあります.

ダランベールの作用素とは,ミンコフスキー空間におけるラプラシアンだと思って良いです.一般に,一次微分形式 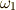 に対し,ダランベール作用素の作用を外微分とホッジ作用素で書けば,次のように表現できます.
に対し,ダランベール作用素の作用を外微分とホッジ作用素で書けば,次のように表現できます.
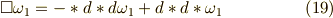
右辺も一次微分形式になっています.式 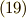 がなりたつことは,練習問題だと思って計算確認してみて下さい.さて,
がなりたつことは,練習問題だと思って計算確認してみて下さい.さて, 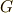 はどうせ外微分を取った形で使うので,何か適当な微分形式の外微分
はどうせ外微分を取った形で使うので,何か適当な微分形式の外微分 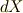 が余分についた
が余分についた 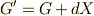 を考えても,
を考えても, 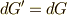 が成り立ってしまうという点に注意しましょう.
が成り立ってしまうという点に注意しましょう. 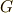 には,少なくとも,一次微分形式に相当するだけの自由度があるということです.(似たような議論が,ベクトル解析の ベクトルポテンシャル , ヘルムホルツの定理 でもあったことも思い出してください.)この自由度を, ゲージ自由度 と呼びます.(難しく考えないで下さい.不定積分の定数と同じことです.)この自由度を逆手に取れば,都合の良い
には,少なくとも,一次微分形式に相当するだけの自由度があるということです.(似たような議論が,ベクトル解析の ベクトルポテンシャル , ヘルムホルツの定理 でもあったことも思い出してください.)この自由度を, ゲージ自由度 と呼びます.(難しく考えないで下さい.不定積分の定数と同じことです.)この自由度を逆手に取れば,都合の良い 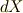 を足し引きしても良いということになります.そこで,
を足し引きしても良いということになります.そこで, 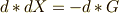 を満たすような
を満たすような 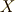 を特に選べば,ダランベールの作用素を
を特に選べば,ダランベールの作用素を 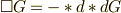 という形にまで簡単化することが出来ます.いつでも簡単化しても良いと言われているのですから,簡単化した方が良いわけで,このようにポテンシャル
という形にまで簡単化することが出来ます.いつでも簡単化しても良いと言われているのですから,簡単化した方が良いわけで,このようにポテンシャル  を選ぶことを『ローレンツゲージを選ぶ』と言います.ローレンツゲージを選べば,ダランベールの作用素を使って,式
を選ぶことを『ローレンツゲージを選ぶ』と言います.ローレンツゲージを選べば,ダランベールの作用素を使って,式 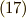 は次の形に書くことが出来ます.
は次の形に書くことが出来ます.
theorem
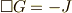
微分形式を使って,マックスウェルの方程式を簡単な形にまとめることを考えてきましたが,微分形式の計算としては,特に何も新しい手法は出てこなかったと思います.途中の計算が分からなかった人は,もう一度該当項目の復習をして下さい.しかし,この話題を通じて,この先きちんと考えないといけない点が少し見えてきました.まず,途中で使った ポアンカレの補題 ですが,私達は,これを数学的にまだきちんと証明していません.この証明には,多様体や閉形式と完全形式といったトピックを勉強しなければなりません.
ここまで,多様体というような概念はわざと避け,ユークリッド空間とミンコフスキー空間だけで微分形式を考えてきましたが,次からはいよいよ多様体上の微分形式を考えます.微分形式の威力と美しさが,読者のみなさんに少しでも伝わっていれば嬉しいです.
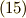 がなりたつことを,実際に計算して確かめてみて下さい.
がなりたつことを,実際に計算して確かめてみて下さい.