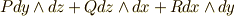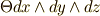線素と体積素と微分形式

面積分に出て来る面積素を二次微分形式で書くと，座標変換して基底ベクトルを変更する際にも，曲面の向き（表・裏）や面積分の向きといった情報を織り込めて便利だということを見ました．例えば，ガウスの発散定理は次のように書けます．

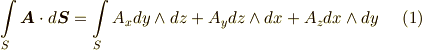
$\int \limits_{S} \bm{A} \cdot d\bm{S}= \int \limits _{S}A_{x}dy \land dz + A_{y}dz \land dx + A_{z}dx \land dy \tag{1}$

これが，二次微分形式であることを確認して下さい．こうなると，線積分や体積分と微分形式の関係も気になるところです．線積分は，線素ベクトルを 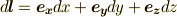$d\bm{l}=\bm{e_{x}}dx+\bm{e_{y}}dy+\bm{e_{z}}dz$ と取れば，次のようにそのまま一次微分形式で表現できます．

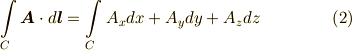
$\int \limits_{C} \bm{A} \cdot d\bm{l}= \int \limits _{C}A_{x}dx + A_{y}dy + A_{z}dz \tag{2}$

体積分の体積素は，基底が直交基底ならば 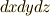dxdydz のように書けますが，より一般的には，基底ベクトルのスカラー三重積で表わされる平行六面体になります．さらに，座標変換によって最初に決めた空間の向き（右手系・左手系）が逆になると，符号も逆になるのでした．（三重積参照．）これは，面積素のときと同様ウェッジ積を使うと，ヤコビアンの符号も織り込むことができて便利です．

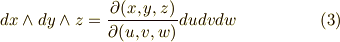
$dx \land dy \land z = \frac{\partial (x,y,z)}{\partial (u,v,w)}dudvdw \tag{3}$

体積分の中身は，三次微分形式で書けることが分かります．

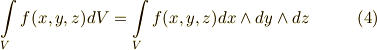
$\int \limits_{V} f(x,y,z) dV= \int \limits _{V}f(x,y,z) dx \land dy \land dz \tag{4}$

[*]	微分形式と，積分の向きの関係は，もう一度微分形式の積分と向きで考えます．いまの段階では，三次元ユークリッド空間で三次微分形式までの例を見ただけですが，外積代数の代数構造が，驚くほど積分計算によく合うという点を実感して頂ければ十分だと思います．外積代数そのものは，線形代数の延長といった議論から出てきたもので，あまり躍動感を感じる数学対象ではありませんでした．高校以来使っている微積分の計算も，図形の問題に応用はできましたが，計算そのものはドライな感じがしていたと思います．微分形式は，代数と幾何学と解析が融合したような分野で，式が本当に活き活きして見えます．

二次微分形式の物理的意味は，物理量に関連させるならば流量に当たるということを面積素と微分形式で触れました．一次微分形式 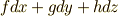fdx+gdy+hdz はスカラー関数と線素の内積と見ることが出来ますので，（ベクトル 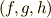(f,g,h) の意味が力とは限りませんが）形式的にベクトル 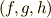(f,g,h) のする仕事と見ることも出来ます．三次微分形式 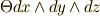$\Theta dx \land dy \land dz$ は，体積素とスカラー場 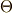$\Theta$ の積ですから，圧縮性流体のように場所によって密度が異なる物体の 密度場 は，このような形を取ると考えても良いでしょう．微分形式が出てきたとき，常にこのような物理的解釈が出来るわけではなりませんが，馴れるまでは，いま触れたような物理量を関連させて覚えておくのも良いかも知れません．

微分形式のイメージ対応表
	表現	代表的な物理的イメージ
一次微分形式		仕事
二次微分形式	$Pdy\land dz +Qdz\land dx +Rdx\land dy$	流量
三次微分形式	$\Theta dx\land dy \land dz$	密度

[home] [微分形式] [ページの先頭]