微分形式の積分と向き
ストークスの定理,ガウスの定理,平面のグリーンの定理などの一般化を考えるための一つの準備として,微分形式の積分と向きという問題を考えておきます.(今まで外微分は考えてきましたが,微分形式の積分には触れませんでした.)向きを保つ座標変換に対して微分形式の積分は不変ですが,向きを変えるような座標変換に対しては符号に注意しなければなりません.同様の注意は,今までにも何度も出てきていますので,特に新しい話題ではありません.
微分形式の積分
領域 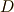 を,
を, 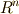 内の有界領域とします.
内の有界領域とします. 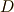 で定義される
で定義される 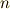 次微分形式
次微分形式 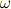 を次のように書きましょう.
を次のように書きましょう.
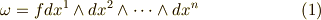
これはつまり,ボリュームフォームです.このとき, 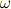 の
の 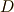 での積分
での積分 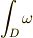 を次のように定義します.
を次のように定義します.
definition
【微分形式の積分】
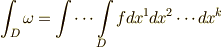
さて,微分形式の微分とも言うべき外微分が座標系によらなかったこと同様,式  で定義した積分も座標系によらないことを示せます.
で定義した積分も座標系によらないことを示せます.
theorem
写像 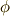 を,領域
を,領域 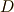 内での向きを保つ写像(向きを保つとはヤコビアンが正ということ)だとし,
内での向きを保つ写像(向きを保つとはヤコビアンが正ということ)だとし, 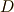 は
は 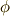 によって領域
によって領域 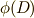 に移されるとします.このとき
に移されるとします.このとき 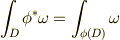 が成り立ちます.
が成り立ちます.
私達は外微分に関して,座標不変性として 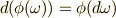 を示しましたが( 外微分の座標不変性 参照),この
を示しましたが( 外微分の座標不変性 参照),この 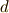 を,積分記号
を,積分記号 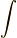 に置き換えたのが上記の定理ですから,積分を微分の逆演算だとすれば,直観的には,定理の主張はいかにも成り立ちそうだと予想できると思います.
に置き換えたのが上記の定理ですから,積分を微分の逆演算だとすれば,直観的には,定理の主張はいかにも成り立ちそうだと予想できると思います.
proof
まず 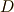 上の座標を
上の座標を 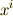 ,
, 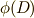 上の座標を
上の座標を 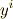 と置きます.写像
と置きます.写像 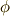 は,
は,  のように働きます
のように働きます  .このとき,
.このとき, 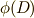 上の微分形式
上の微分形式 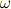 を
を 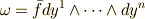 と定義します.
と定義します. 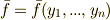 です.
です. 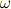 に対して
に対して 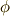 の引き戻し
の引き戻し 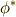 を考えると( 微分形式の引き戻し1 参照),
を考えると( 微分形式の引き戻し1 参照), 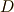 上の微分形式
上の微分形式 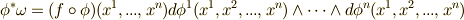 を得ます.ここで,
を得ます.ここで, 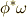 の基底については
の基底については 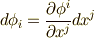 と書けて,まとめると
と書けて,まとめると 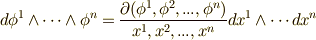 とヤコビアンを使った形に出来ます.(要するに基底の座標変換です. ウェッジ積の座標変換 を参照にして下さい.)このヤコビアンを
とヤコビアンを使った形に出来ます.(要するに基底の座標変換です. ウェッジ積の座標変換 を参照にして下さい.)このヤコビアンを 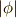 と書くと,結局,
と書くと,結局, 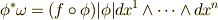 が成り立ちます.この両辺の積分を取ると,積分の定義(式
が成り立ちます.この両辺の積分を取ると,積分の定義(式 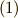 )より,
)より, 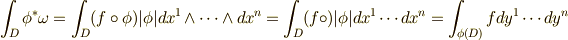 となり,定理が示されます.■
となり,定理が示されます.■
証明の最後の段,最後の式変形は,重積分の積分変数を変換しただけです.(ヤコビアンで変数変換し,積分範囲もそれに伴って変更したわけです.)微分形式の積分を式 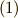 のように定義したので,自然に重積分の公式を使って,変数と積分範囲を変更できたわけですが,この定理に関して注意すべき点があります.
のように定義したので,自然に重積分の公式を使って,変数と積分範囲を変更できたわけですが,この定理に関して注意すべき点があります.
わざと証明の中で明示的に言わなかったので,少し引っ掛かって欲しかったのですが,途中で出てきたヤコビアン 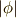 は,いま前提として『向きを保つ変換』だけを考えているので定理のようになるのです.空間の向きを逆にする座標変換なら,符号が逆になりますので注意して下さい.
は,いま前提として『向きを保つ変換』だけを考えているので定理のようになるのです.空間の向きを逆にする座標変換なら,符号が逆になりますので注意して下さい.
| [*] | もっとも,今後は主に向きを保つ変換だけを考えて行きますので,この注意を喚起するのも今だけかも知れません. |