もう一度grad,div,rot
三次元ユークリッド空間上の零次微分形式 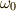 ,一次微分形式
,一次微分形式 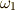 ,二次微分形式
,二次微分形式  ,三次微分形式
,三次微分形式 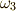 の 外微分 は,それぞれ次のようになるのでした.(まだ計算に馴れていない人は,練習問題だと思って左辺から右辺を導いてみて下さい.)
の 外微分 は,それぞれ次のようになるのでした.(まだ計算に馴れていない人は,練習問題だと思って左辺から右辺を導いてみて下さい.)
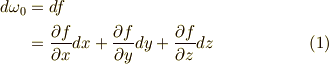
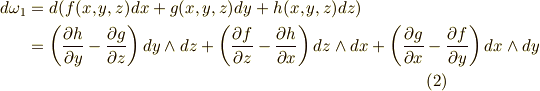
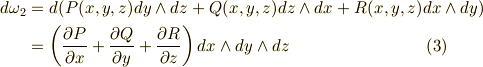
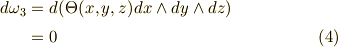
これらをじっと見ていて気がつくのは,ベクトル解析に出てきた  ,
,  ,
, 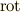 等の演算に, 似ている ということです.式
等の演算に, 似ている ということです.式 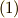 は単なる関数の全微分なので良いとして,まず式
は単なる関数の全微分なので良いとして,まず式 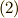 から検討してみましょう.これは,ベクトルの 回転 に似ています.一次微分形式を
から検討してみましょう.これは,ベクトルの 回転 に似ています.一次微分形式を  と書き,
と書き, 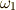 を
を 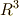 のベクトルに対応させる写像
のベクトルに対応させる写像 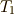 を導入します.
を導入します.

このとき,ベクトル 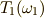 の回転は次のように表わされます.
の回転は次のように表わされます.
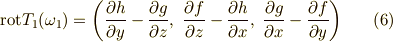
成分はよく似ていますが,式 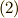 は二次微分形式になっていますので,まず ホッジ作用素 を使って一次微分形式に対応させたあと,
は二次微分形式になっていますので,まず ホッジ作用素 を使って一次微分形式に対応させたあと, 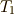 を作用させる必要があります.こうすれば,
を作用させる必要があります.こうすれば, 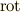 を外微分とホッジ作用素だけで表現できる事がわかります.
を外微分とホッジ作用素だけで表現できる事がわかります.
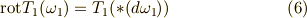
同様に,発散と二次微分形式は次のように関係づけられます.式 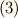 と 発散 を見ながら,自分で確認してみて下さい.
と 発散 を見ながら,自分で確認してみて下さい.
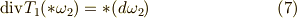
勾配は次のように書けるでしょう.

初めて勉強したとき,何だか謎めいて見えたベクトル演算子ですが,微分形式を使うことで,統一的に見ることが出来そうですね.素敵です.
| [*] | ホッジ作用素については,空間の向きや計量の正負について注意点がたくさんありました.いま,(文脈から)常識的に,三次元ユークリッド空間で, 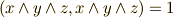 と向きを付けました.今後も,三次元ユークリッド空間で考えている限り,このように向き付けることにします. と向きを付けました.今後も,三次元ユークリッド空間で考えている限り,このように向き付けることにします. |
ベクトル場とか接ベクトルとか・・・
勾配,発散,回転などは,ベクトル演算子 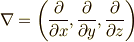 の作用として与えられましたが, 共変ベクトルと反変ベクトル の記事で見たように,普通のベクトルは反変ベクトルで,
の作用として与えられましたが, 共変ベクトルと反変ベクトル の記事で見たように,普通のベクトルは反変ベクトルで,  は共変ベクトルだということでした.つまり,普通のベクトルと
は共変ベクトルだということでした.つまり,普通のベクトルと  は双対ベクトルの関係にあるわけです.
は双対ベクトルの関係にあるわけです.
この関係を外積空間で捉えなおしてみましょう. ホッジ作用素 で触れたように, 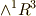 の双対空間は
の双対空間は 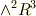 ですから,普通のベクトル
ですから,普通のベクトル 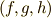 を前セクションのように
を前セクションのように 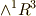 に関係づけるなら,
に関係づけるなら,  は
は 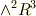 に関係づけられることになります.
に関係づけられることになります.
一次微分形式 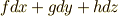 の双対は,
の双対は, 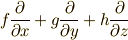 と書け,これは
と書け,これは 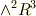 の元です.普通の対応では,基底は
の元です.普通の対応では,基底は 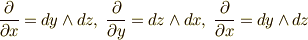 と考えて良いです.
と考えて良いです.
| [†] | この段階では,  等を偏微分の記号とは見ずに,単にベクトルの基底と考えたほうが正確です.しかし,偏微分の記号と全然関係の無い記号をわざと紛らわしく使うはずはなく,これを偏微分の記号と考えて良いのです.数学の厳密な本には,『これは偏微分ではなくて単に基底だ』と書いてある場合がありますが,それは(微分という演算が定義できるかによらないとか)論理的にうるさいことを言っているだけです.細かい理屈は,多様体を勉強し始めてから考えたいと思いますので,今は自然な解釈をしていて良いと思います. 等を偏微分の記号とは見ずに,単にベクトルの基底と考えたほうが正確です.しかし,偏微分の記号と全然関係の無い記号をわざと紛らわしく使うはずはなく,これを偏微分の記号と考えて良いのです.数学の厳密な本には,『これは偏微分ではなくて単に基底だ』と書いてある場合がありますが,それは(微分という演算が定義できるかによらないとか)論理的にうるさいことを言っているだけです.細かい理屈は,多様体を勉強し始めてから考えたいと思いますので,今は自然な解釈をしていて良いと思います. |
実は,普通に(曲面 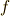 上の局所的な
上の局所的な  座標系で)考える ベクトル場 は,
座標系で)考える ベクトル場 は, 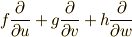 のような形に考えるのが自然なことです.(例えば
のような形に考えるのが自然なことです.(例えば 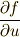 という偏微分は,曲面
という偏微分は,曲面 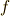 の
の  軸にそった変化を与える作用素ですから,向きとしては
軸にそった変化を与える作用素ですから,向きとしては 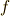 上で定義される
上で定義される  軸の方向を向いていると考えることが出来ます.そこで,
軸の方向を向いていると考えることが出来ます.そこで, 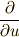 を基底
を基底 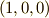 に対応させるのは自然なことですよね.)一般に,
に対応させるのは自然なことですよね.)一般に, 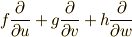 の形のベクトルを 接ベクトル と呼びますが,これは,また,多様体を勉強した後に稿を改めて解説するつもりです.とりあえず,滑らかな曲面上の接ベクトルは, 方向微分 と同じものだと考えても間違えではありません.(同じものです.)蛇足ですが,接ベクトルと双対の関係にあるベクトルを, 余接ベクトル と呼びますが,先ほどのように二次微分形式を接ベクトル場に対応させるなら,一次微分形式は余接ベクトル場に対応することになります.これも,多様体を勉強した後で詳しく説明する予定です.(名前はごっついですが,図的なイメージさえ湧けば,そんなに難しい話ではないと思います.)
の形のベクトルを 接ベクトル と呼びますが,これは,また,多様体を勉強した後に稿を改めて解説するつもりです.とりあえず,滑らかな曲面上の接ベクトルは, 方向微分 と同じものだと考えても間違えではありません.(同じものです.)蛇足ですが,接ベクトルと双対の関係にあるベクトルを, 余接ベクトル と呼びますが,先ほどのように二次微分形式を接ベクトル場に対応させるなら,一次微分形式は余接ベクトル場に対応することになります.これも,多様体を勉強した後で詳しく説明する予定です.(名前はごっついですが,図的なイメージさえ湧けば,そんなに難しい話ではないと思います.)
| [‡] | 一次微分形式は 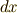 などが基底になっていて,いかにも積分して欲しそうな形をしています.一方,ベクトル場は二次微分形式だと書きましたが, などが基底になっていて,いかにも積分して欲しそうな形をしています.一方,ベクトル場は二次微分形式だと書きましたが,  などを基底としていて,右から何かが掛かって来るのを待ち構えており,微分したい形です.こんなところにも,何だか微分と積分という双対風(?)な関係が垣間見えます.素敵です. などを基底としていて,右から何かが掛かって来るのを待ち構えており,微分したい形です.こんなところにも,何だか微分と積分という双対風(?)な関係が垣間見えます.素敵です. |
| [§] | ベクトル場の基底と 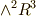 の基底の対応は,自明なわけではありません.空間の向きの取り方によります. の基底の対応は,自明なわけではありません.空間の向きの取り方によります. |
| [¶] | もし二つの座標系  と と  に関し, に関し, 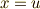 であれば,常に であれば,常に  は成り立ちます.このことは, 外微分の座標不変性 で見たように,座標変換 は成り立ちます.このことは, 外微分の座標不変性 で見たように,座標変換  に際し,例えば一次微分形式なら に際し,例えば一次微分形式なら  が成り立つという,外微分の座標不変性という性質として知られるものです.(一般の次数の微分形式も座標不変性を確認できます.) しかし,一つの基底だけを抜き出して,例えば が成り立つという,外微分の座標不変性という性質として知られるものです.(一般の次数の微分形式も座標不変性を確認できます.) しかし,一つの基底だけを抜き出して,例えば 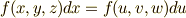 が成り立ついうことは一般には言えません.ベクトルの和の形になっているからこそ,不変なんですね.これは,偏微分に関して が成り立ついうことは一般には言えません.ベクトルの和の形になっているからこそ,不変なんですね.これは,偏微分に関して 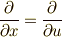 が一般には成り立たず,変換は が一般には成り立たず,変換は 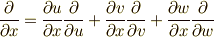 のように表現しなければならないことと対応しています. ベクトルの関数 , gradの積分形による定義 などで, のように表現しなければならないことと対応しています. ベクトルの関数 , gradの積分形による定義 などで,  の各成分は座標変換に対して不変ではない,という注意を強調しましたが,これは前述の理由によるものです.結局,『ベクトルそのものは座標系と関係ないが,ベクトル成分は座標系による』という話で,言われてみれば当然です. の各成分は座標変換に対して不変ではない,という注意を強調しましたが,これは前述の理由によるものです.結局,『ベクトルそのものは座標系と関係ないが,ベクトル成分は座標系による』という話で,言われてみれば当然です. |