微分形式
いよいよ,微分形式と呼ばれる量を導入します.こんなものを使って何が嬉しいのかということは,次の 面積素と微分形式 以降の記事で徐々に明らかにするとこにして,この記事ではまず定義を与え,少し先走って幾つか重要な点に概略的に触れることにします.(この段階で全て理解しなくても大丈夫です.)
また,当面の間,三次元ユークリッド空間 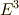 の中だけで話を進めることにします.三次元ユークリッド空間とは,私達が「普通に」三次元として知っている空間で,小学校以来,空間図形を考えるのに使っていた空間です.少し正確に言えば,三次元ユークリッド空間とは,三つの独立な座標成分を決めることで空間内の点の位置を一意的に指定でき,二点
の中だけで話を進めることにします.三次元ユークリッド空間とは,私達が「普通に」三次元として知っている空間で,小学校以来,空間図形を考えるのに使っていた空間です.少し正確に言えば,三次元ユークリッド空間とは,三つの独立な座標成分を決めることで空間内の点の位置を一意的に指定でき,二点  間の距離が
間の距離が 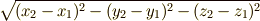 で与えられるような空間のことです.ユークリッド空間を表わすにはユークリッド
で与えられるような空間のことです.ユークリッド空間を表わすにはユークリッド 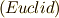 の頭文字と次元を表わす指数を使って
の頭文字と次元を表わす指数を使って 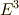 と書いたり,混乱の恐れが無い場合には,成分が実数であることを示すために,単に
と書いたり,混乱の恐れが無い場合には,成分が実数であることを示すために,単に 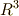 と書いたりします.以下の議論では,特に断らない限り,全てユークリッド空間上の話だとします.
と書いたりします.以下の議論では,特に断らない限り,全てユークリッド空間上の話だとします.
| [*] | 三次元ユークリッド空間で一番普通なのは直交座標を取ることです.三次元ユークリッド空間が一つあれば,全世界をカバーできる,というのは少し自己中心的な見方です.そのうち,もう少し謙虚に,少なくとも自分の近所だけがユークリッド空間になっている,と考えることで多様体という概念を導入します.しばらくは,一般の多様体上の微分形式は考えず,全てユークリッド空間上の話だとしますが,この枠組みにおいては,私達は,お釈迦様の手の平の中で飛んでいる孫悟空のような物なのだと,何となく心に刻んでおいて下さい.そのうちに,もっと座標系に関しては視野を広げていきます. |
外積代数の復習
私達は,テンソル空間に次のようなルールを導入することで外積代数という代数を得ました.(ルールの導入とは,つまりテンソル空間を イデアルで類別 したところ,その商代数の元の間に次のような演算規則が入ったということです.)
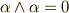
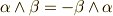 (交代性)
(交代性)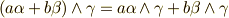 (分配則)
(分配則)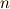 次元ベクトル空間
次元ベクトル空間 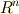 に対して,
に対して, 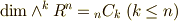 (
(  ).(外積空間の次元)
).(外積空間の次元)
ここで行われている乗法  を ウェッジ積 もしくは 外積 と呼ぶのでした.いま,三次元のベクトル空間
を ウェッジ積 もしくは 外積 と呼ぶのでした.いま,三次元のベクトル空間 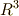 の独立な基底を
の独立な基底を 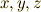 とすると,外積代数
とすると,外積代数 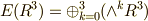 の独立な基底は,次のものだけになります.
の独立な基底は,次のものだけになります.
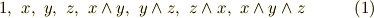
それ以外の積の形は,例えば  のように同じ元を含むウェッジ積はルール1により
のように同じ元を含むウェッジ積はルール1により  になってしますますし,四つ以上の元のウェッジ積
になってしますますし,四つ以上の元のウェッジ積  などは,ルール4により同様に
などは,ルール4により同様に  になります.(また
になります.(また 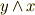 などはルール2により,
などはルール2により, 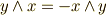 が言えて本質的には
が言えて本質的には 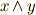 と同じになります.)ここまでは,まだ外積代数の復習です.
と同じになります.)ここまでは,まだ外積代数の復習です.
微分形式
ここで一工夫して, 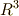 として,微小量
として,微小量  が張るベクトル空間
が張るベクトル空間 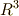 を考えます.このとき,
を考えます.このとき,  上のベクトル値関数を 微分形式 と呼びます.この空間で独立な基底は,以下のものになります.階数別に示します.
上のベクトル値関数を 微分形式 と呼びます.この空間で独立な基底は,以下のものになります.階数別に示します.

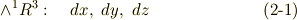
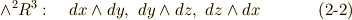
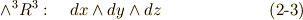
| [†] |  は単なる実数 は単なる実数 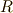 です.実数体は, です.実数体は, 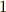 を基底にするベクトル空間だと見ることも出来ますよね. を基底にするベクトル空間だと見ることも出来ますよね. |
これらを基底とするベクトル関数が微分形式です.ウェッジ積の次数に注意しましょう.例えば,次のような関数は, 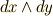 のような
のような 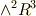 の基底を持つ微分形式ですので, 二次微分形式 と呼ばれます.
の基底を持つ微分形式ですので, 二次微分形式 と呼ばれます. 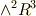 (これもベクトル空間)の基底の一次結合になっていますから,確かにベクトルですね.
(これもベクトル空間)の基底の一次結合になっていますから,確かにベクトルですね.
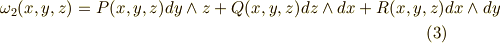
次の形のものは, 一次微分形式 です.  の元です.
の元です.

次の形のものは 三次微分形式 です. 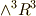 の元ですね.
の元ですね.

また,テンソル解析でスカラーのことを  次のテンソルだと考えたのと同様,単なる関数を 零次微分形式 と定義します.(
次のテンソルだと考えたのと同様,単なる関数を 零次微分形式 と定義します.(  を基底とする,
を基底とする,  の元だと考えれば,この定義は極めて自然なものだと言えます.)
の元だと考えれば,この定義は極めて自然なものだと言えます.)
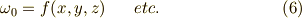
三次元ユークリッド空間上の微分形式の定義はここまでです.骨格は外積代数と同じなので,それほど難しい点は無かったと思いますが,もう一度,まとめておきます.
definition
- 【零次微分形式】
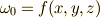 (関数)
(関数)- 【一次微分形式】
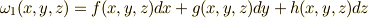
- 【二次微分形式】
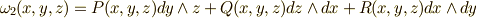
- 【三次微分形式】

次のセクションに注意点と,これから勉強するポイントをまとめておきます.
| [‡] | 関数(  次微分形式)と 次微分形式)と 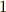 次以上の微分形式の積は, 次以上の微分形式の積は, 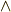 とは書かず,従来のように何も書かないか とは書かず,従来のように何も書かないか  で書きます. で書きます. |
| [§] | 細かいことを言えば,このセクションで考えたように,外積代数の枠組みで考える微分形式を,詳しくは交代微分形式と呼びます.外積代数は,一般のテンソル積 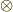 に交代性を加えて得られる代数なわけですが, に交代性を加えて得られる代数なわけですが,  のように対称性を満たすようにテンソル積から考えたものを対称微分形式と呼んで区別するからです.もっとも,交代性微分形式の理論が非常に強力で応用性も高いため,普通は微分形式と言えば交代性微分形式のことをだけを指すことが多いようです. のように対称性を満たすようにテンソル積から考えたものを対称微分形式と呼んで区別するからです.もっとも,交代性微分形式の理論が非常に強力で応用性も高いため,普通は微分形式と言えば交代性微分形式のことをだけを指すことが多いようです. |
ポイント1
上の例では,三次元ベクトル空間 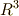 から生成した微分形式を考えたので,三次までしか出てきませんでした.もし,一般に
から生成した微分形式を考えたので,三次までしか出てきませんでした.もし,一般に 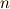 次元のベクトル空間から外積代数を生成するなら,
次元のベクトル空間から外積代数を生成するなら, 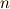 次微分形式までが出てきます.この先,しばらくは高次元の微分形式を考えることは無いと思いますが,一応,定義だけは示しておきます.
次微分形式までが出てきます.この先,しばらくは高次元の微分形式を考えることは無いと思いますが,一応,定義だけは示しておきます. 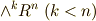 の元である
の元である 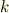 次微分形式は,次のように定義されます.
次微分形式は,次のように定義されます.
【 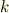 次微分形式】
次微分形式】

ただし, 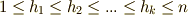 とし,
とし, 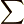 は,全ての可能な
は,全ての可能な 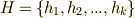 の組み合わせについての総和を意味するものとします.高次元の例として,電磁気学の基礎方程式である マックスウェルの方程式 を,ミンコフスキー空間(四次元)で考えてみる予定です.
の組み合わせについての総和を意味するものとします.高次元の例として,電磁気学の基礎方程式である マックスウェルの方程式 を,ミンコフスキー空間(四次元)で考えてみる予定です.
ポイント2
ベクトル空間の基底として,なぜいきなり 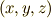 ではなく,
ではなく,  を取ったかという疑問を持っている人がいると思います.もしくは,何が違うんだ?と思っている人がいると思います.簡単に言えば,これは,いま考えている座標系
を取ったかという疑問を持っている人がいると思います.もしくは,何が違うんだ?と思っている人がいると思います.簡単に言えば,これは,いま考えている座標系  が局所的なものだという立場の表明です.どっかの点の近くに,チョコッと設定した座標系だ,というイメージでしばらくは乗り切りましょう.
が局所的なものだという立場の表明です.どっかの点の近くに,チョコッと設定した座標系だ,というイメージでしばらくは乗り切りましょう.
| [¶] | 教科書によっては,『  などはベクトル空間の形式的な基底とする』と書いているものがあります. などはベクトル空間の形式的な基底とする』と書いているものがあります.  などは,今まで微積分に出てきた記号ですから,普通なら微積分に関係ありそうだと思うのに,『単に形式的なものだ』と断るのは,いかにも愛想が無いように思います.本当のことを言えば,これらを微積分に出てきた微小量だと思って良く,実際,これから微積分をたくさんします.なんと言っても,外積空間という線形代数の延長に出てきたような概念に,微積分が美しく導入されるという点が微分形式の魅力なのです.数学者が,この辺りで無愛想な理由は,恐らく,私達が,まだ などは,今まで微積分に出てきた記号ですから,普通なら微積分に関係ありそうだと思うのに,『単に形式的なものだ』と断るのは,いかにも愛想が無いように思います.本当のことを言えば,これらを微積分に出てきた微小量だと思って良く,実際,これから微積分をたくさんします.なんと言っても,外積空間という線形代数の延長に出てきたような概念に,微積分が美しく導入されるという点が微分形式の魅力なのです.数学者が,この辺りで無愛想な理由は,恐らく,私達が,まだ 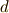 で定義される"外微分"という操作を定義していないからだと思います. で定義される"外微分"という操作を定義していないからだと思います. 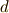 という記号に,そっと耳を当ててみましょう.『早く という記号に,そっと耳を当ててみましょう.『早く 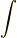 をつけて積分してくれ〜!』という微分形式の叫びが聞こえてきそうです. をつけて積分してくれ〜!』という微分形式の叫びが聞こえてきそうです. |
ポイント3
微小量の普通の積 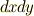 や
や  と(これらは 面積分 や 体積分 に出てきました),微分形式の基底
と(これらは 面積分 や 体積分 に出てきました),微分形式の基底 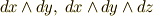 の大きな違いは,前者では積に順番が関係ないのに対し,後者では,外積代数のルールにより,積の順序を変えると符号も変わることです.
の大きな違いは,前者では積に順番が関係ないのに対し,後者では,外積代数のルールにより,積の順序を変えると符号も変わることです.
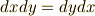
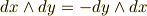
また,普通の積では  ですが,微分形式では
ですが,微分形式では  となってしまいます.(この話題は 微小量の積 で取り上げます.)ポイント2の註で,微分形式はこれから積分に威力を発揮する,と書きましたが,こんな性質を組み込んで,一体どんな場面で威力を発揮するというのでしょうか?その具体的な場面を少し考えてみましょう.
となってしまいます.(この話題は 微小量の積 で取り上げます.)ポイント2の註で,微分形式はこれから積分に威力を発揮する,と書きましたが,こんな性質を組み込んで,一体どんな場面で威力を発揮するというのでしょうか?その具体的な場面を少し考えてみましょう.
今までに勉強した内容で,ベクトル解析の積分公式には『積分の向き』が問題になるような状況がたくさんありました.線積分では曲線を辿る向きが,面積分では曲面の法線ベクトルの向きが,そして体積分では基底ベクトルが右手系か左手系かによって決まる符号がありました.微分形式の交代性を利用すれば, 向きや符号の問題を綺麗に織り込んで ,今までよりもずっと簡単で美しい形で表現することが可能になります.これが,微分形式を導入する醍醐味の一つです.
| [#] | そもそも,外積代数はテンソル代数の特別な場合(交代形式)だと見ることが出来ましたから,そのような視点から見れば,微分形式とは,交代形式のテンソル代数に解析学を組み込んだものだと見ることも出来ます.後で示すように,微分形式は共変テンソルだと見ることが出来ますから,テンソル解析が得意な人はその知識を役に立つと思います. |
ポイント4
外積代数には出てこなかった新しい概念に, 外微分 があります. 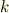 次微分形式の外微分は
次微分形式の外微分は  次微分形式になる,というように,外微分によって微分形式の次数が一つ上がります.
次微分形式になる,というように,外微分によって微分形式の次数が一つ上がります. 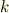 次微分形式と
次微分形式と  次微分形式は,それぞれ
次微分形式は,それぞれ 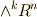 と
と 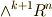 という異なるベクトル空間の元でしたから,外微分はベクトル空間の写像だと考えることが出来ます.名前の通り,微分の仲間だと考えて良いのですが,ベクトル空間の写像という見方も明確にしておいた方が良いと思います.
という異なるベクトル空間の元でしたから,外微分はベクトル空間の写像だと考えることが出来ます.名前の通り,微分の仲間だと考えて良いのですが,ベクトル空間の写像という見方も明確にしておいた方が良いと思います.
| [♠] | 外積代数だけでも面白い代数構造をしてはいましたが,微積分の話題が関係無くて,なんだか静的でした.微分形式になると,俄然,微分したり積分したりと活気が出てきます.微分形式は,線形代数と微積分がちょうど合わさる,三陸沖のような豊かな漁場だと考えても良いでしょう.物理学や工学への応用も色々あります. |
今のところ,  などについている
などについている 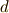 は単に微小量であることを表わすための記号ですが,実はこれは全微分を表わす記号
は単に微小量であることを表わすための記号ですが,実はこれは全微分を表わす記号 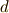 と同じです.外微分とは全微分を拡張したものなのです.初めて微積分を勉強したとき,
と同じです.外微分とは全微分を拡張したものなのです.初めて微積分を勉強したとき, 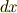 などは必ず
などは必ず 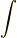 とセットに使う,単に積分記号を明示するためだけの記号のように思った人が多いと思います.(著者も,高校生のときはよく
とセットに使う,単に積分記号を明示するためだけの記号のように思った人が多いと思います.(著者も,高校生のときはよく 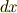 を書き忘れていました.)しかし,微分形式の理論では,ベクトル空間の基底としての
を書き忘れていました.)しかし,微分形式の理論では,ベクトル空間の基底としての 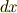 という幾何学的意味と,従来の解析的意味での
という幾何学的意味と,従来の解析的意味での 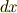 が見事に融合してきます.記号
が見事に融合してきます.記号 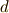 が,新たな意味を得て,本当に活き活きと活躍し始めます.楽しみです.
が,新たな意味を得て,本当に活き活きと活躍し始めます.楽しみです.
外微分については,おいおい勉強するとして,この外微分には, 座標系によらない という著しい特徴があります.この性質を用いれば,座標系の取り方に関係なく,微分方程式を記述することが出来そうです.微分形式を導入する最大の旨味は,この 座標不変性 という点にあり,これによって今まで煩わされてきた座標系(テンソル解析の添字の嵐を思い出してください)から離れて,非常にシンプルな形で微分方程式を記述できるようになるのです.そして,座標系から離れて,より一般的な多様体という世界へ視野を広げて行くにも,微分形式はちょうどよい入り口になると思います.外積代数だけでは,こうした見方は出来ません.外積代数に外微分という概念を組み合わせてはじめて拓けてきた,新しい物の見方です.
| [♥] | もちろん,ベクトルやテンソルだって,その『実体』ともいうべき存在は座標系のとりかたとは無関係です.しかし,どうしても添字がたくさん出てきて,面倒くさい感じになってしまいます.交代形式で書いても良いなら,微分形式で書いた方がすっきり見通しよく表現できるわけです.微分形式と同じ計算をテンソルを使って行うことも可能なはずで,座標系の取り方によらない事も,微分形式だけの性質ではありません.微分形式の特長は,その美しさにあると思います. |