リー微分のイメージ(ベクトルによるベクトルのリー微分)
この記事では,ベクトルによるベクトルのリー微分を説明します.
![\mathcal{L}_X Y = [X,Y] \tag{1}](./73b7f14c8a315de1254bd49bb81a7de2.png)
と書かれても,よく分からず途方に暮れた人は多いのではないでしょうか? リー微分は分かってしまえば簡単です.
二つの流れを用意する
二次元平面上の二つの流れを用意します.
まず, 微分幾何学における流れの具体例 で取り扱った放物線状のベクトル場 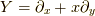 と,
と, 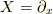 と言う,
と言う,  軸の正の方向に単位量だけ流れている流れを用意します.
軸の正の方向に単位量だけ流れている流れを用意します.
ここで,
![\mathcal{L}_X Y &= [X,Y] \\&= \dfrac{\partial}{\partial x} \left( \dfrac{\partial}{\partial x} + x \dfrac{\partial}{\partial y} \right)- \left( \dfrac{\partial}{\partial x} + x \dfrac{\partial}{\partial y} \right) \left( \dfrac{\partial}{\partial x} \right) \\&= \left( \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial}{\partial y} + x \dfrac{\partial^2}{\partial x \partial y} \right)-\left( \dfrac{\partial^2}{\partial x^2} + x \dfrac{\partial^2}{\partial x \partial y} \right) \\&= \dfrac{\partial}{\partial y} \tag{2}](./47bd7f6b2875171bce168df377d681a1.png)
となりました.これは,何を表しているかと言うと, 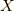 の流れに単位量だけ乗った後
の流れに単位量だけ乗った後 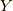 の流れに単位量だけ乗った結果から,
の流れに単位量だけ乗った結果から, 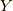 の流れに単位量だけ乗った後
の流れに単位量だけ乗った後 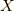 の流れに単位量だけ乗った結果を引いたベクトルを表しています.
の流れに単位量だけ乗った結果を引いたベクトルを表しています.
図を見れば明らかでしょう.
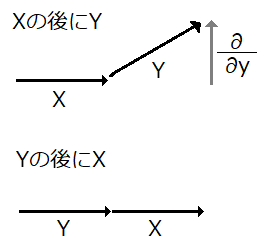
これは,参考文献にもある通りです.  も
も 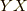 も二階の微分を含むのでベクトルではないのですが,
も二階の微分を含むのでベクトルではないのですが, 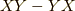 はうまく相殺して一階の微分となっていることに注意して下さい.実はこの記事はリー微分の全てではなくて,多様体上のリー微分になると,基底である
はうまく相殺して一階の微分となっていることに注意して下さい.実はこの記事はリー微分の全てではなくて,多様体上のリー微分になると,基底である 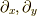 等の変換も扱わねばならないようです.僕が理解した時には追って報告しようと思います.今日はここまで,お疲れさまでした.
等の変換も扱わねばならないようです.僕が理解した時には追って報告しようと思います.今日はここまで,お疲れさまでした.