SU(2)のリー群とリー環について
この記事ではパウリ行列
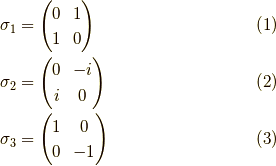
とリー群 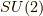 ,リー環
,リー環 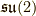 の関係についてまとめます.
記号は パウリ行列のwikipedia に合わせます.
の関係についてまとめます.
記号は パウリ行列のwikipedia に合わせます.
リー環について
リー環 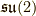 はリー群のパラメータの無限小変化量に当たります.
(後で示すので,まだわからなくて大丈夫です.)
これが,パウリ行列を使うとうまく表せます.
はリー群のパラメータの無限小変化量に当たります.
(後で示すので,まだわからなくて大丈夫です.)
これが,パウリ行列を使うとうまく表せます.
今回はパウリ行列をそのまま使わないで,ちょっと小細工をして,
全てに  を掛けます.
を掛けます.
すると,
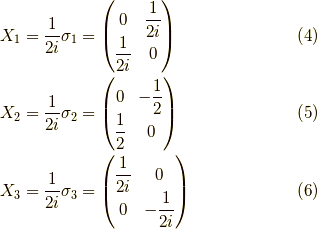
となります.これらがリー環 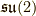 の全ての基底
です.
の全ての基底
です.  を掛けると何がうれしいかというと,交換子
を掛けると何がうれしいかというと,交換子 ![[A,B]=AB-BA](./161b8209ebbef19abbef34c502deb03f.png) について,
について,
![[X_1,X_2] =X_3 \tag{7} \\[X_2,X_3] =X_1 \tag{8} \\[X_3,X_1] =X_2 \tag{9}](./96b51e3cce467adebb67dc70b6cb08a0.png)
ときれいな関係になります.だから何?と言われそうですが,この辺のことに関しては EMANさんの解説 を見るといいんじゃないでしょうか?
特殊ユニタリー群 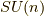 に対応するリー環
に対応するリー環 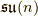 の元
の元  は一般に
は一般に

を満たします.上付きの 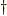 は物理よりの書き方で,複素共役を取って転置したものを
表します.
は物理よりの書き方で,複素共役を取って転置したものを
表します.  がこれらの関係を満たすことを確認してみてください.
この性質(式(10)と式(11))を言葉でいうと,トレースがゼロの歪エルミート行列と言います.
がこれらの関係を満たすことを確認してみてください.
この性質(式(10)と式(11))を言葉でいうと,トレースがゼロの歪エルミート行列と言います.
リー群について
リー群の元 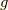 とはリー環の元
とはリー環の元 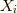 の線形結合の指数関数を取ったものです.
行列(例えば
の線形結合の指数関数を取ったものです.
行列(例えば 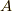 とする)の指数関数ということで,
とする)の指数関数ということで,  を単位行列として,
を単位行列として,
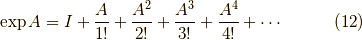
となります.ここで 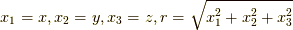 として,
として,
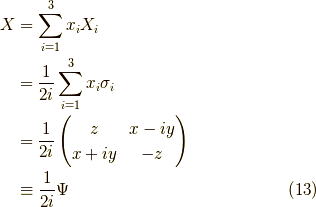
ここで(  )は
)は 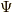 の定義を示すものと
します.
の定義を示すものと
します.  です.
です.
ここで,リー環の指数関数を取ってリー群の元 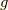 を求めてみましょう.
を求めてみましょう.
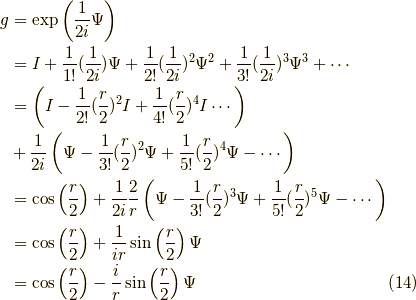
よって,  の成分表示をすると,
の成分表示をすると,
ここで, 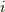 以外は実数ですから,
以外は実数ですから, 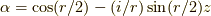 ,
, 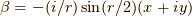 と置くと,
と置くと,

ここで  は複素共役です.
は複素共役です.
SU(2)の定義
一方で, 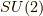 の定義として,
の定義として,

となります.この定義に従った元が式(16)と一致することを見ましょう. 式(17)から,
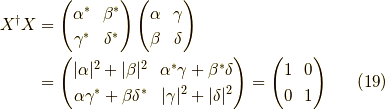
また,式(18)から,
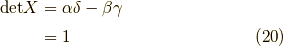
よって,式(19)と(20)より,

この連立方程式を行列で書くと,
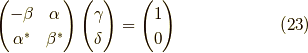
ここで式 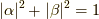 を使って
,
を使って
, 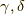 について解くと,
について解くと,
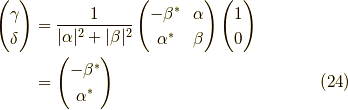
よって,

となり,式(16)に一致することがわかりました.
さて,僕がこの記事を書く切っ掛けを話しておきます.
式(25)について,今までの変数の設定をリセット
して,  とします.
すると,式(25)は
とします.
すると,式(25)は
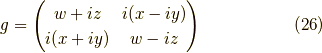
この形はリー環と似ています.
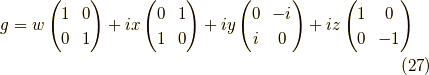
なんだ?パウリ行列に 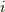 が掛かっている?
単位行列も加わっているぞ?なんて,混乱されないでください.
あくまでこれがリー群
が掛かっている?
単位行列も加わっているぞ?なんて,混乱されないでください.
あくまでこれがリー群 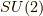 の元の一般形であって,
パウリ行列
の元の一般形であって,
パウリ行列 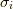 とより強く関係しているのは,リー環
とより強く関係しているのは,リー環 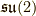 の方
です.まあ,
の方
です.まあ, 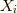 にした時に
にした時に 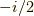 を掛けていますけれどね.
ややこしいですけれど,リー環では単位行列は含まないのは決定的な違いです.
また,式(25)について
を掛けていますけれどね.
ややこしいですけれど,リー環では単位行列は含まないのは決定的な違いです.
また,式(25)について 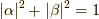 は注意です.
は注意です.
リー環トレースゼロの反エルミート行列  に対応する
のは,リー群デターミナント1のユニタリー行列
に対応する
のは,リー群デターミナント1のユニタリー行列 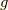 って訳ですね.
って訳ですね.
最後に
ちょっと話が変わりますが,自分が確かなイメージを持っている例で,
リー群の無限小変化がリー環になる.と言うことを説明します.
リー環 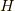 として,リー群の元
として,リー群の元 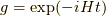 を対応
させます.
を対応
させます. 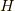 とした理由は量子論のハミルトニアンを意識しています.
ここで
とした理由は量子論のハミルトニアンを意識しています.
ここで 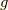 から
から 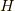 を求めるには,
を求めるには, 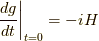 として求まるわけ
です.
として求まるわけ
です. 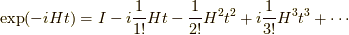 ですから,
テイラー展開の1次の項を求めているわけです.
つまり,リー群のパラメータ
ですから,
テイラー展開の1次の項を求めているわけです.
つまり,リー群のパラメータ 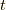 の微小変化の接線(1次変化)の変化方向をリー環と呼んでいるわけです.
の微小変化の接線(1次変化)の変化方向をリー環と呼んでいるわけです.
それでは今日はここまで,お疲れさまでした!