リー環の随伴表現とは
リー環とは
リー環,もしくは,同じものですがリー代数 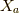 において,交換子から定まる構造定数
において,交換子から定まる構造定数 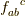 を
次の様に定めます.
を
次の様に定めます.
![[X_a,X_b] = i f_{ab}^{ \ \ c} X_c \tag{1}](./b84c356feabe12ef0ad20f9c81e04419.png)
ここで, 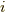 は虚数単位で,交換子は
は虚数単位で,交換子は ![[X_a,X_b] = X_a X_b - X_b X_a](./52bc2bff4451b2300547f6f96482c017.png) を表します.
また,アインシュタインの縮約規則を用いて,
を表します.
また,アインシュタインの縮約規則を用いて,  は全ての元にわたる和です.
は全ての元にわたる和です.
リー環というと,特定の代数演算の関係が決められた抽象的な
代数ですが,それと同じ関係を満たす行列で具体的に表すことができます.
その代数の行列化をリー環の「表現」と言います.
表現にはいろいろな種類がありますが,その中で今回は随伴表現 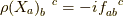 というものを紹介します.
ここで,
というものを紹介します.
ここで, 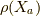 は表現(行列)で
は表現(行列)で 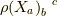 は行列の成分で
は行列の成分で  は行列の行,
は行列の行,  は行列の列を指定します.
不思議な事にこれは元のリー環の一つの表現になっているのです.
は行列の列を指定します.
不思議な事にこれは元のリー環の一つの表現になっているのです.
ヤコビ積
リー環には,交換子からなるヤコビ恒等式があります. それは,
![Z = [X_a,[X_b,X_c]] + [X_a,[X_b,X_c]] + [X_a,[X_b,X_c]] = 0 \tag{2}](./c43c45f4bf11e37b765f3bd7691c8f8f.png)
という任意のリー環に対して恒等的に成り立つ関係式です.
ただし,右辺の 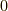 はリー環のゼロ元です.
この関係は,実際に行列を持ち出すことなく,
代数的に展開してやれば,確認できます.
はリー環のゼロ元です.
この関係は,実際に行列を持ち出すことなく,
代数的に展開してやれば,確認できます.
さて,式  を式
を式  の関係を用いて,
変形していきましょう.
の関係を用いて,
変形していきましょう.
![[X_a,[X_b,X_c]] &= [X_a,i f_{bc}^{ \ \ d} X_d] \\&= i f_{bc}^{ \ \ d} [X_a,X_d] \\&= i^2 f_{bc}^{ \ \ d} f_{ad}^{ \ \ e} X_e \\&= - f_{bc}^{ \ \ d} f_{ad}^{ \ \ e} X_e\tag{3}](./3259ddc28a80a5da4a7eddc5356c0a39.png)
の様に計算していくと,ヤコビ恒等式は,

ここで,任意の  に対して,上式は成立するので,
に対して,上式は成立するので, 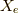 を除いて,
を除いて,
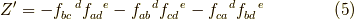
随伴表現
さて,随伴表現との対応を見てみましょう.

の様に決めると,式 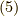 は,
は,

ここで全体の符号を反転させて, 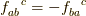 の関係を使うと(これは構造定数が交換子から作られていて,
の関係を使うと(これは構造定数が交換子から作られていて, ![[X_a,X_b] = - [X_b,X_a]](./d50f50e63f66c944d602fe95530a3781.png) であることから出ます.),
であることから出ます.), 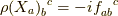 より
より 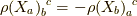 が言えるので,
が言えるので,
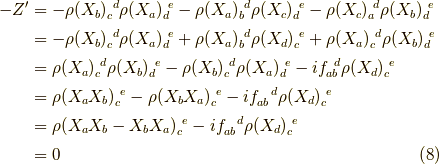
となり,よって,
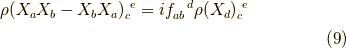
ですから,これは,リー環が満たす代数関係
![[X_a,X_b] = X_a X_b - X_b X_a = i f_{ab}^{ \ \ d} X_d\tag{10}](./af25761d4a7daa82357da9af1ee9a3a4.png)
に対応しています.(単連結な)リー代数の構造は構造定数によって,
完全に決定されます.よって, 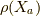 はリー環の表現だと分かります.
はリー環の表現だと分かります.
具体例(su(2)とso(3))
最後に具体例として,同じ構造定数を持つ 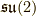 と
と 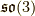 の随伴表現を
見て終わりにします.その構造定数は例えば,パウリ行列
の随伴表現を
見て終わりにします.その構造定数は例えば,パウリ行列 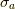 が
が
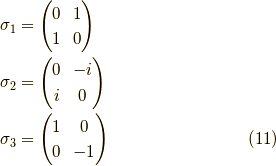
で,

とすれば,
![[X_1,X_2] &= i X_3 \\[X_2,X_3] &= i X_1 \\[X_3,X_1] &= i X_2 \tag{13}](./fd6eef56f018282a2a2ea3c5ff708d64.png)
より,ゼロにならないのは,
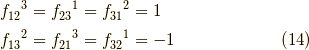
と分かるので,随伴表現の行列 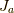 は,
は,
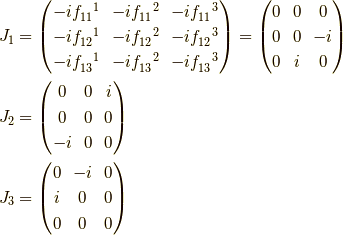
より,随伴表現が表現として成立しているか確かめると, 確かに例えば,
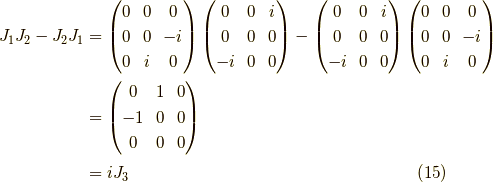
となり,確かに元のリー代数と同じ構造定数を持つ表現になっていることが分かります.