井戸型ポテンシャルの数値解
home > 計算物理学 >目次
目的
井戸型ポテンシャルの中の粒子のシュレディンガー方程式を数値的に解いてみます. 井戸型ポテンシャルは
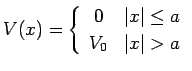
というポテンシャル V で与えられるものです. このポテンシャルのシュレディンガー方程式,つまりただの微分方程式の数値解を求め, グラフィクスライブラリ PGPLOT で固有状態の波動関数を出力してみます.
定常状態の(時間に依存しない)シュレディンガー方程式は
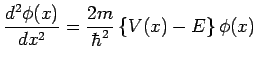
ですが,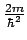 はただの定数なので,
はただの定数なので,
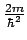 = 1 として計算します.
規格化もしていません.固有値はどのように計算すれば数値的に求められるのか,
固有値によって波動関数がどんな形になるのか調べてみましょう.
= 1 として計算します.
規格化もしていません.固有値はどのように計算すれば数値的に求められるのか,
固有値によって波動関数がどんな形になるのか調べてみましょう.
コーディング
では,早速ソースコードの紹介です.
アルゴリズム
微分方程式を解くアルゴリズムとして「オイラー・クロマー法」 とやらを使ってみました(手元の本に載ってたから). アルゴリズムはつぎの通りです.
- x の範囲を幅 Δx の区間に分割し,整数 s に対して,
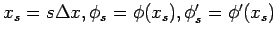 という記号を用いる.
という記号を用いる.
- φ(x) のパリティを決め,
パリティが偶の解に対しては φ(0) = 1 , φ′(0) = 0 と選び,
パリティが奇の解に対しては φ(0) = 0 , φ′(0) = 1 と選ぶ.
0 でない φ(0) または φ′(0) の解は任意.
-
固有関数 E の値を推定する.
- アルゴリズム
を用いて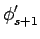
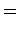
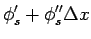
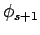
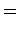
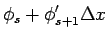
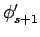 と
と
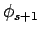 を計算する.
を計算する.
-
φ(x) が発散するまで x を大きくしながら φ(x) の反復計算を行う.
- 固有値 E を変化させて,手順 4 から 5 を繰り返す.E の値を変化させながら,E をわずかに小さくした場合には φ が正または負のどちらか一方に発散し,それよりもわずかに大きくした場合には逆に発散するような限界点を定める.
ソースコード
オイラー・クロマー法を使ったシュレディンガー方程式の計算を実際にコーディングするとつぎのようになりました.
このプログラムを書くにあたって 計算物理学入門 の eigen.c を大変参考にさせていただきました.
グラフィクスの処理は PGPLOT を使用しているので, このコードをコンパイル,実行するには PGPLOT ライブラリがインストールされている必要があります.
1 /* =====================================================================
2 井戸型ポテンシャルの固有値を計算しグラフィック出力 Jan 12 2003
3 ===================================================================== */
4
5
6
7 #include <stdio.h>
8 #include <math.h>
9 #include "cpgplot.h"
10
11
12
13 /* ---------------------------------------------------------------------
14 potential function V(x)
15 --------------------------------------------------------------------- */
16
17 double V(double x, double V0, double a)
18 {
19 double potential;
20 if( fabs(x) > a )
21 potential = V0;
22 else
23 potential = 0.0;
24 return ( potential );
25 }
26
27
28
29 /* ---------------------------------------------------------------------
30 parity check
31 --------------------------------------------------------------------- */
32
33 void ParityCheck( int parity, double *phi, double *dphi )
34 {
35 if(parity == -1)
36 {
37 *phi = 0; // initial values at x = 0
38 *dphi = 1; // first derivative
39 }
40 else
41 {
42 *phi = 1;
43 *dphi = 0;
44 }
45 }
46
47
48
49 /* ---------------------------------------------------------------------
50 Euler algorithm
51 --------------------------------------------------------------------- */
52
53 void Euler( double V0, double a, double x,
54 double dx ,double E ,double *dphi, double *phi )
55 {
56 double d2phi;
57
58 // 2m/hbar^2 = 1 となる無次元の単位系で計算。
59 d2phi = (V( x, V0, a) - E) * (*phi);
60
61 // オイラー-クロマー・アルゴリズム
62 *dphi += d2phi * dx;
63 *phi += *dphi * dx;
64 }
65
66
67
68 /* ---------------------------------------------------------------------
69 井戸型ポテンシャルの描画 (青線)
70 --------------------------------------------------------------------- */
71
72 void DrawPotential( double a, double V0, double xmax )
73 {
74 cpgsci(4); cpgslw(1);
75 cpgmove( -xmax, V0 );
76 cpgdraw( -a, V0 );
77 cpgdraw( -a, 0 );
78 cpgdraw( a, 0 );
79 cpgdraw( a, V0 );
80 cpgdraw( xmax, V0 );
81 }
82
83
84
85 /* ---------------------------------------------------------------------
86 main
87 --------------------------------------------------------------------- */
88
89 int main(void)
90 {
91 double V0, a, dx;
92 double E, deltaE, d2phi, dphi, phi, x;
93 double x_old, phi_old, xmax, bottom, top;
94 int parity, i;
95
96 // 物理的設定
97 V0 = 4.0;
98 a = 4.0;
99 printf( "Parity = ?\n" ); scanf( "%d", &parity );
100 //parity = 1;
101
102 // 計算設定
103 dx = 0.001;
104 deltaE = 0.0002;
105
106 // 固有値Eの推定値
107 E = .1;
108 printf( "E = ?\n" ); scanf( "%lf", &E );
109
110 // パリティにより phi, dphi の初期値を決定
111 ParityCheck( parity, &phi, &dphi );
112
113 for(;;){
114 x = 0;
115 // 大きな x までオイラー法を繰り返す
116 while( x <= 6 ){
117 Euler( V0, a, x, dx, E, &dphi, &phi);
118 x += dx;
119 }
120 // 大きな x で phi がほぼ 0 となるようにEを決める
121 if( fabs(phi) < 0.02 ) break;
122 // Eの値を deltaE だけ変え, 波動関数を初期値に戻し, 計算を繰り返す
123 E += deltaE;
124 ParityCheck( parity, &phi, &dphi );
125 }
126
127 printf("Eigen value = %lf\n", E);
128
129 // グラフ描画設定
130 xmax = 6.0;
131 bottom = 3.0;
132 top = 5.0;
133
134 cpgopen( "/xserv" );
135 cpgpap( 5.0, 1.0 );
136 cpgenv( -xmax, xmax, -bottom, top, 0, 0 );
137
138 // 井戸型ポテンシャルの描画
139 DrawPotential( a, V0, xmax);
140
141 // 固有値の描画
142 cpgsci(2); cpgmove( -a, E ); cpgdraw( a, E);
143
144 // 波動関数 phi の描画(白線)
145 x = 0; ParityCheck( parity, &phi, &dphi );
146 cpgsci(1); cpgslw(1);
147 while( x<=xmax ){
148 x_old = x;
149 phi_old = phi;
150 x += dx;
151 // グラフを描くため、再びオイラー法を使う
152 Euler( V0, a, x, dx, E , &dphi, &phi);
153 cpgmove( x_old, phi_old ); cpgdraw( x, phi );
154 cpgmove( -x_old, phi_old * parity ); cpgdraw( -x, phi * parity );
155 }
156
157 cpgclos();
158
159 return 0;
160 }
波動関数の収束は 112 〜 124 で決めています. x が少し大きい点で 波動関数 phi がはぼ 0 となる E を固有値としています. でもこれはいいかげんな処理です.判定の値は何度か計算して,経験的に決定しました. 本当は「調和振動子ポテンシャルの数値解」でやっているように決めるのがいいです.
実行結果
V0 = 4.0, a = 4.0 の井戸型ポテンシャルで,E の推定値と parity を変えながら, 基底状態から第4励起状態までの固有値と波動関数を計算.赤線は固有値の値です.
基底状態
計算したエネルギー固有値:E = 0.121600
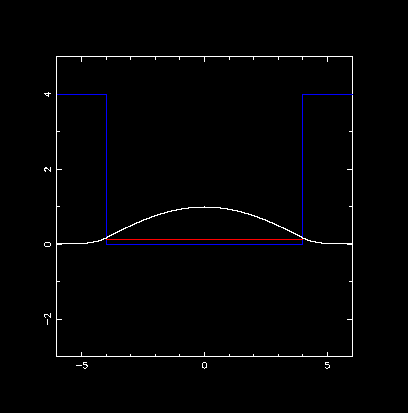
第1励起状態
計算したエネルギー固有値:E = 0.485000
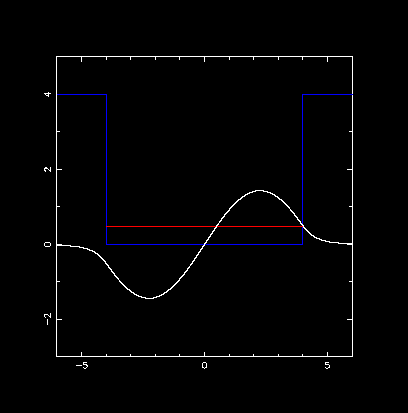
第2励起状態
計算したエネルギー固有値:E = 1.083600
第3励起状態
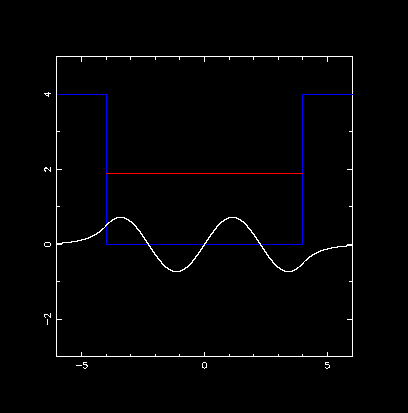
計算したエネルギー固有値:E = 1.905600
第4励起状態
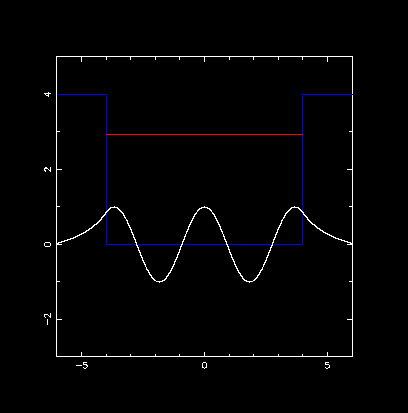
計算したエネルギー固有値:E = 2.923000
基底状態の E を E1, 第1励起状態の E をE2,… とすると
E3/E1 = 8.91 ≒ 32
E4/E1 = 15.67 ≒ 42
E5/E1 = 24.04 ≒ 52
基底状態との比がだいたい n2となります.