波動関数を数値計算で規格化

home > 計算物理学 >
[サイトマップ]

目次

規格化

これまでいくつかのポテンシャルでシュレディンガー方程式を数値的に解き， 波動関数と固有値を求めてきましたが，波動関数の規格化は行っていませんでした． 実際に意味のある値を計算するためには、波動関数の規格化が必要になってきます．

波動関数の規格化については こちら をご覧ください．

数値計算での規格化

規格化するにはまず，全空間で波動関数の絶対値の二乗を積分する必要があります． しかし数値計算で求めた波動関数では，全空間で正確な値を求めることはできません． 下のように，ある程度の x のところまでいくと誤差がたまって波動関数は発散してしまいます．

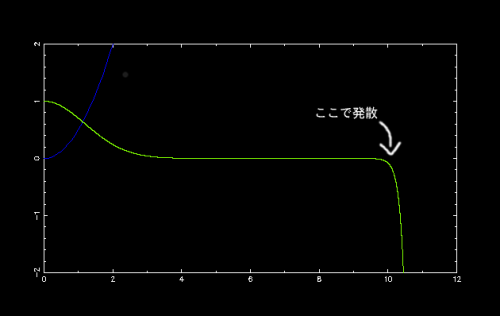
波動関数の発散の図

ですから，発散する直前までの区間で波動関数を積分します． 波動関数がほとんど収束した時点で打ちきり，そこまでの範囲で数値積分を行います．

物理設定

解析解が分かっている調和振動子のシュレディンガー方程式を数値的に解いて，波動関数を規格化してみます． 調和振動子の数値計算は 以前にもやりました が， 今回は計算しやすいようにパラメータを変更します．

1次元調和振動子のシュレディンガー方程式

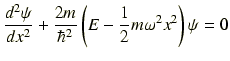
$\displaystyle \frac{d^2 \psi}{dx^2} + \frac{2m}{\hbar^2}\left(E-\frac{1}{2}m\omega^2 x^2\right)\psi = 0$

において

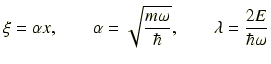
$\displaystyle \xi = \alpha x,\qquad \alpha=\sqrt{\frac{m\omega}{\hbar}},\qquad \lambda=\frac{2E}{\hbar\omega}$

という置きかえをします．するとシュレディンガー方程式は

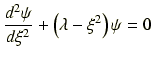
$\displaystyle \frac{d^2 \psi}{d\xi^2} + \left(\lambda-\xi^2\right)\psi = 0$

となり，さらに

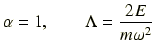
$\displaystyle \alpha=1,\qquad \Lambda=\frac{2E}{m\omega^2}$

と置きかえると

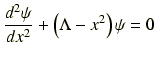
$\displaystyle \frac{d^2 \psi}{dx^2} + \left(\Lambda-x^2\right)\psi = 0$

となります．この方程式を数値的に解き，波動関数を規格化します．

コーディング

アルゴリズム

微分方程式はこれまでと同じ様にルンゲ・クッタ法で解きます．固有値の求め方もこれまでと同じです． 規格化にあたっては，つぎの方針をとります．

  1. 波動関数が発散する点を求める
  2. 原点から発散点までの区間で波動関数を数値積分
  3. 積分値のルート分の1を波動関数に掛ける

原点から十分離れた点では，波動関数は収束してゼロになるはずです． しかし数値計算ではそうはならず，上述したように原点から遠ざかるといつか発散してしまいます． そうなる前に，波動関数がある程度ゼロに近づいた点で切り捨て，収束したことにします． そのためにあるしきい値を決めておきます． 波動関数が収束しはじめて，しきい値以下の値になったらそこを発散点とします．

数値積分には簡単かつ精度の良い台形法を用います．

ソースコード

いきあたりばったりで書いたので無駄が多いっぽいです．

[normalize.c]

     1	/* =====================================================================
     2	   調和振動子ポテンシャルの波動関数を規格化
     3	   Last modified: Dec 19 2003
     4	   ===================================================================== */
     5	#include <stdio.h>
     6	#include <math.h>
     7	#include "cpgplot.h"
     8	
     9	/* 物理設定 */
    10	static double E    =  0.0;  /* 固有値 */
    11	static double dE   =  -1.0;
    12	static int parity  =  1;
    13	
    14	/* ルンゲ・クッタ法のきざみ幅 */
    15	static double h = 0.001;
    16	
    17	
    18	
    19	/* --------------------------------------------------------------------- 
    20	   ポテンシャル関数
    21	   --------------------------------------------------------------------- */
    22	double V(double x)
    23	{
    24	  /* V(x)=x^2 */
    25	  return pow(x,2);
    26	}
    27	
    28	
    29	
    30	/* ---------------------------------------------------------------------
    31	   導関数の定義
    32	   --------------------------------------------------------------------- */
    33	double dpsi(double x, double psi, double z)
    34	{
    35	  /* \frac{d\psi}{dx} = z */
    36	  return(z);
    37	}
    38	
    39	double dz(double x, double psi, double z)
    40	{
    41	  /* \frac{dz}{dx} = (V(x)-E)\psi */
    42	  return( (V(x) - E) * psi );
    43	}
    44	
    45	
    46	
    47	/* ---------------------------------------------------------------------
    48	   固有値を求める・波動関数を規格化する
    49	   --------------------------------------------------------------------- */
    50	void ravelAndNormalize(double x0, double psi0, double z0, double h){
    51	  double x, psi, z, k[4], q[4], psi_old, psi_tmp;
    52	  double is_converge_start = 4.0;  /* 発散評価の開始点 */
    53	  double is_converge_value = 0.00001;  /* 発散評価のしきい値 */
    54	  double converge_point;  /* 発散点 */
    55	  double integral;  /* 半区間での (波動関数)^2 の積分値 */
    56	  double A;  /* 規格化因子 */
    57	  int decimal = 14;  /* 計算する小数点以下の桁数 */
    58	  int i, j, n;
    59	  int loop = decimal/h;
    60	  int color = 9;
    61	  
    62	  /* 固有値Eの決定 */
    63	  for (n=1 ; n<decimal ; n++) {
    64	    dE = -1 * dE/10; 
    65	    /* 波動関数初期化 */
    66	    x = x0; psi = psi0, z = z0;
    67	    while (1) {
    68	      for (i=1 ; i<=loop ; i++) { 
    69		/* 4次のルンゲ・クッタ法の連立式 */
    70		k[0] = h * dpsi(x, psi, z);
    71		q[0] = h * dz  (x, psi, z);
    72		k[1] = h * dpsi(x+h/2, psi+k[0]/2, z+q[0]/2);
    73		q[1] = h * dz  (x+h/2, psi+k[0]/2, z+q[0]/2);
    74		k[2] = h * dpsi(x+h/2, psi+k[1]/2, z+q[1]/2);
    75		q[2] = h * dz  (x+h/2, psi+k[1]/2, z+q[1]/2);
    76		k[3] = h * dpsi(x+h, psi+k[2], z+q[2]);
    77		q[3] = h * dz  (x+h, psi+k[2], z+q[2]);
    78		psi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
    79		z   += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
    80		/* 次のきざみ幅へ */
    81		x = x0 + i * h;
    82	      }
    83	      /* 今回と前回のpsiを保存 */
    84	      psi_old = psi_tmp; 
    85	      psi_tmp = psi;
    86	      /* 今回と前回のpsiが異符号になれば while(1) を抜ける
    87		 i=1ではpsi_oldの値が無意味なので比較しない */
    88	      if ( (i>1) && ((psi_old > 0) && (psi < 0)) ) break;
    89	      if ( (i>1) && ((psi_old < 0) && (psi > 0)) ) break;
    90	      printf("E = %2.12lf\n", E);  /* モニタ */
    91	      /* 固有値変更 */
    92	      E += dE;
    93	      /* 波動関数初期化 */
    94	      x = x0; psi = psi0, z = z0;
    95	    }
    96	  }
    97	  
    98	  /* 規格化する前の (波動関数)^2 の描画・発散点の決定 */
    99	  x = x0; psi = psi0, z = z0;
   100	  for (i=1 ; i<=loop ; i++) { 
   101	    k[0] = h * dpsi(x, psi, z);
   102	    q[0] = h * dz  (x, psi, z);
   103	    k[1] = h * dpsi(x+h/2, psi+k[0]/2, z+q[0]/2);
   104	    q[1] = h * dz  (x+h/2, psi+k[0]/2, z+q[0]/2);
   105	    k[2] = h * dpsi(x+h/2, psi+k[1]/2, z+q[1]/2);
   106	    q[2] = h * dz  (x+h/2, psi+k[1]/2, z+q[1]/2);
   107	    k[3] = h * dpsi(x+h, psi+k[2], z+q[2]);
   108	    q[3] = h * dz  (x+h, psi+k[2], z+q[2]);
   109	    /* PGPLOT */
   110	    cpgsci(color);
   111	    cpgmove(x,     pow(psi,2));
   112	    cpgdraw(x+h/6, pow(psi+k[0]/6,2));
   113	    cpgsci(color);
   114	    cpgmove(x+h/6, pow(psi+k[0]/6,2));
   115	    cpgdraw(x+h/2, pow(psi+k[1]/2,2));
   116	    cpgsci(color);
   117	    cpgmove(x+h/2,   pow(psi+k[1]/2,2));
   118	    cpgdraw(x+h*5/6, pow(psi+k[2]*5/6,2));
   119	    cpgsci(color);
   120	    cpgmove(x+h*5/6, pow(psi+k[2]*5/6,2));
   121	    cpgdraw(x+h,     pow(psi+k[3],2));
   122	    psi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
   123	    z   += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
   124	    /* 次のきざみ幅へ */
   125	    x = x0 + i * h;
   126	    /* 発散点の決定 */
   127	    if ( (x>is_converge_start) && (fabs(psi)<is_converge_value) ) {
   128	      converge_point = x;
   129	      break;
   130	    }
   131	  }
   132	
   133	  /* 原点から発散点までの区間で (波動関数)^2 を積分 */ 
   134	  x = x0; psi = psi0, z = z0;
   135	  integral = 0.0;
   136	  psi_tmp = psi0;
   137	  for (i=1 ; i<=loop ; i++) { 
   138	    k[0] = h * dpsi(x, psi, z);
   139	    q[0] = h * dz  (x, psi, z);
   140	    k[1] = h * dpsi(x+h/2, psi+k[0]/2, z+q[0]/2);
   141	    q[1] = h * dz  (x+h/2, psi+k[0]/2, z+q[0]/2);
   142	    k[2] = h * dpsi(x+h/2, psi+k[1]/2, z+q[1]/2);
   143	    q[2] = h * dz  (x+h/2, psi+k[1]/2, z+q[1]/2);
   144	    k[3] = h * dpsi(x+h, psi+k[2], z+q[2]);
   145	    q[3] = h * dz  (x+h, psi+k[2], z+q[2]);
   146	    psi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
   147	    z   += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
   148	    /* 次のきざみ幅へ */
   149	    x = x0 + i * h;
   150	    /* 台形の面積を足し合わせる */
   151	    psi_old = psi_tmp; 
   152	    psi_tmp = psi;
   153	    integral += ( ( pow(psi_old,2) + pow(psi,2) ) * h ) / 2;
   154	    /* 発散点まできたら終了 */
   155	    if (x>converge_point)
   156	      break;
   157	  }
   158	  
   159	  /* 規格化因子 */
   160	  A = 1 / sqrt(2*integral);
   161	  
   162	  /* 規格化した (波動関数)^2 の描画 */
   163	  x = x0; psi = psi0, z = z0, color=2;
   164	  for (i=1 ; i<=loop ; i++) { 
   165	    k[0] = h * dpsi(x, psi, z);
   166	    q[0] = h * dz  (x, psi, z);
   167	    k[1] = h * dpsi(x+h/2, psi+k[0]/2, z+q[0]/2);
   168	    q[1] = h * dz  (x+h/2, psi+k[0]/2, z+q[0]/2);
   169	    k[2] = h * dpsi(x+h/2, psi+k[1]/2, z+q[1]/2);
   170	    q[2] = h * dz  (x+h/2, psi+k[1]/2, z+q[1]/2);
   171	    k[3] = h * dpsi(x+h, psi+k[2], z+q[2]);
   172	    q[3] = h * dz  (x+h, psi+k[2], z+q[2]);
   173	    /* PGPLOT */
   174	    cpgsci(color);
   175	    cpgmove(x,     pow(A*psi,2));
   176	    cpgdraw(x+h/6, pow(A*(psi+k[0]/6),2));
   177	    cpgsci(color);
   178	    cpgmove(x+h/6, pow(A*(psi+k[0]/6),2));
   179	    cpgdraw(x+h/2, pow(A*(psi+k[1]/2),2));
   180	    cpgsci(color);
   181	    cpgmove(x+h/2,   pow(A*(psi+k[1]/2),2));
   182	    cpgdraw(x+h*5/6, pow(A*(psi+k[2]*5/6),2));
   183	    cpgsci(color);
   184	    cpgmove(x+h*5/6, pow(A*(psi+k[2]*5/6),2));
   185	    cpgdraw(x+h,     pow(A*(psi+k[3]),2));
   186	    psi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
   187	    z   += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
   188	    /* 次のきざみ幅へ */
   189	    x = x0 + i * h;
   190	    /* 発散点まできたら終了 */
   191	    if (x>converge_point)
   192	      break;
   193	  }
   194	
   195	  /* 計算結果表示 */
   196	  printf(" E = %2.12lf\n 収束点 = %2.12lf\n 積分値 = %2.12lf\n |psi(0)|^2 = %2.12lf\n",
   197		 E, converge_point, 2*integral, pow(A*psi0,2));
   198	}
   199	
   200	
   201	
   202	/* ---------------------------------------------------------------------
   203	   調和振動子ポテンシャルの描画(青線)  V(x)=x^2
   204	   --------------------------------------------------------------------- */
   205	void DrawPotential(double xmax)
   206	{
   207	  double i;
   208	  cpgsci(4); cpgslw(1);
   209	  cpgmove(-xmax, pow(xmax,2));
   210	  for (i=-xmax; i<xmax ; i+=0.1) {
   211	    cpgdraw(i, pow(i,2));
   212	  }
   213	}
   214	
   215	
   216	
   217	/* ---------------------------------------------------------------------
   218	   main
   219	   --------------------------------------------------------------------- */
   220	int main(void)
   221	{
   222	  double psi0, z0;
   223	  double xmax, bottom, top;
   224	
   225	  /* グラフ描画設定 */
   226	  xmax   = 6.0;
   227	  bottom = 2.0;
   228	  top    = 2.0;
   229	
   230	  /* PGPLOT */
   231	  cpgopen("/xserv");
   232	  cpgpap(6.0, 0.6);
   233	  cpgenv(0, xmax, -bottom, top, 0, 0);
   234	
   235	  /* パリティチェック */
   236	  if (parity==-1) {  /* 奇関数 */
   237	    psi0=0.0; z0=1.0;
   238	  }
   239	  else {  /* 偶関数 */
   240	    psi0=1.0; z0=0.0; 
   241	  }
   242	
   243	  DrawPotential(xmax);
   244	  ravelAndNormalize(0.0, psi0, z0, h);
   245	
   246	  cpgclos();
   247	  return 0;
   248	}
   249	
   250	
   251

87，88行目で決定した固有値を使って，126行目で発散点を求めています． 発散点を評価するしきい値 is_divvalue は53行目で 0.00001 という値に設定しています．

また，発散の評価は is_divstart より大きい x でのみ行います． これは準位が高くなると波動関数が波打って節が出てくるためです． is_divstart の値は一度グラフを書いてから目分量で決めました．今の場合は 4.0 です．

原点から発散点までの積分は，ルンゲ・クッタ法のきざみ幅をそのまま使って， 150から152行目で台形の面積を足し合わせることで積分しています．pow(phi,2) は波動関数の二乗です． はじめは二乗するのを忘れていて，うまく規格化因子が求まりませんでした (^^;

規格化因子は161行目で計算しています．このプログラムでは半区間しか計算していないので， ルートをとる前に積分値 integral を2倍しています．

175から186行目では，グラフ描画の際に規格化因子を波動関数の値に掛けています．

実行結果

プログラムを実行すると，Xwindowにグラフ，標準出力に数値が出力されます．グラフ出力はつぎの様になります．

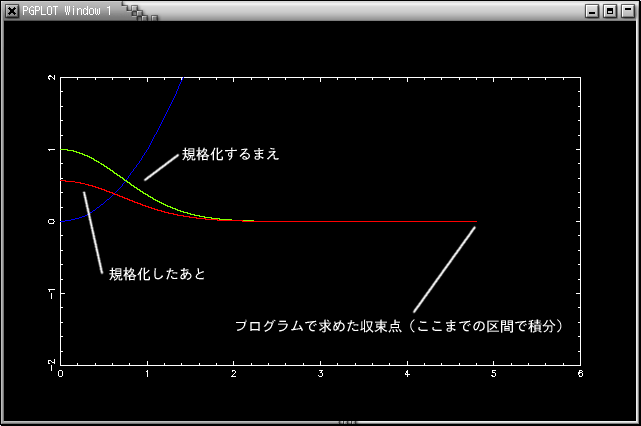
緑は規格化するまえの波動関数の二乗，赤は規格化したあとの波動関数の二乗をプロットしたものです． 青いのは調和振動子ポテンシャルの形です．

プログラム中の E, dE, parity の値を変えながら，基底状態から第4励起状態まで計算しました．以下に結果を並べます．

基底状態

E = 1.000000000000
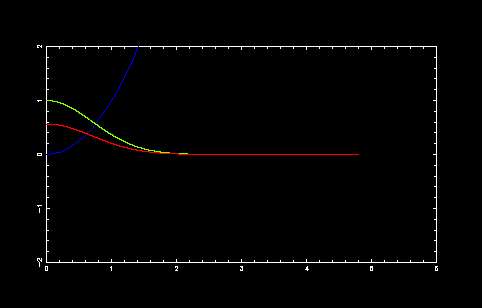
収束点 = 4.799000000000
積分値 = 1.772453850885
|psi(0)|^2 = 0.564189583554

第1励起状態

E = 3.000000000000
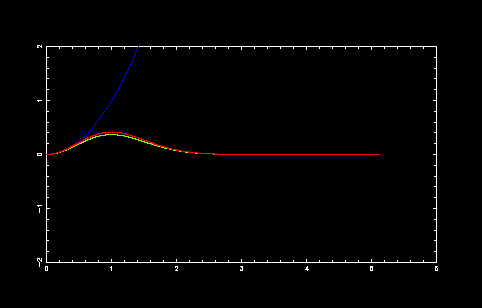
収束点 = 5.128000000000
積分値 = 0.886226925433
|psi(0)|^2 = 0.000000000000

第2励起状態

E = 5.000000000001
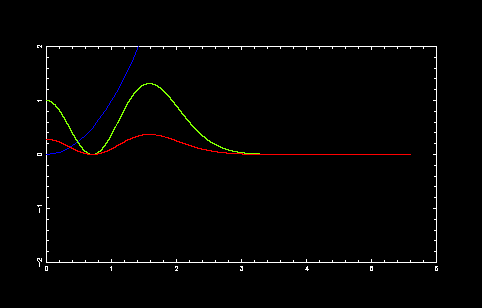
収束点 = 5.592000000000
積分値 = 3.544907701793
|psi(0)|^2 = 0.282094791775

第3励起状態

E = 7.000000000002
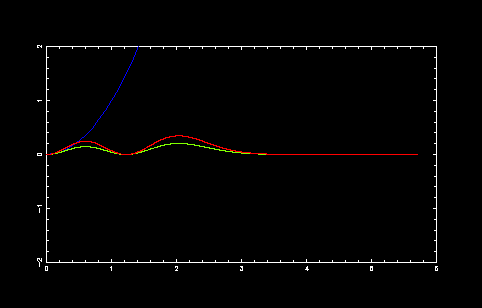
収束点 = 5.708000000000
積分値 = 0.590817950283
|psi(0)|^2 = 0.000000000000

第4励起状態

E = 9.000000000004
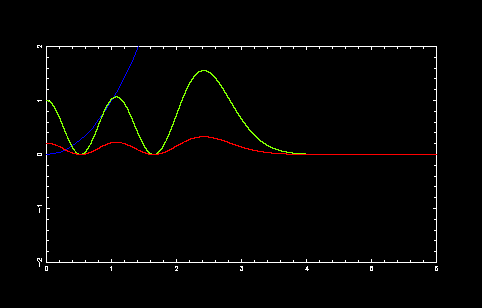
収束点 = 6.164000000000
積分値 = 4.726543602398
|psi(0)|^2 = 0.211571093831

評価

数値計算で求めた規格化因子を解析解と比較します．解析解では，規格化因子は

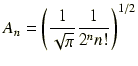
$\displaystyle A_n = \left(\frac{1}{\sqrt{\pi}}\frac{1}{2^n n!}\right)^{1/2}$

となっています．また，規格化された波動関数は

$\displaystyle \psi_n(x) = A_n e^{-1/2}H_n(x)$

です．ここで $ H_n(x)$ はエルミートの多項式で，

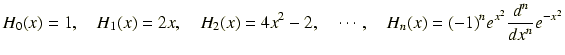
$\displaystyle H_0(x)=1,\quad H_1(x)=2x,\quad H_2(x)=4x^2-2,\quad\cdots, \quad H_n(x) = (-1)^ne^{x^2}\frac{d^n}{dx^n}e^{-x^2}$

というものです．基底状態は n = 0 の場合ですから，規格化された波動関数は

$\displaystyle \psi_0(x)$ $\displaystyle = A_0 e^{-x/2} H_0(x)$
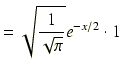
$\displaystyle = \sqrt{\frac{1}{\sqrt{\pi}}}e^{-x/2}\cdot1$

となります．e0 = 1 ですから，x = 0 の点では

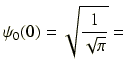基底状態： $\displaystyle \psi_0(0) = \sqrt{\frac{1}{\sqrt{\pi}}} =$ 0.751125544465

という値になります．同様に第1励起状態から第4励起状態まで，規格化された波動関数の x = 0 での値を求めると，

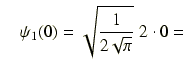第1励起状態： $\displaystyle \quad \psi_1(0) = \sqrt{\frac{1}{2\sqrt{\pi}}}\ 2\cdot0 =$ 0
第2励起状態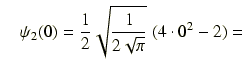： $\displaystyle \quad \psi_2(0) = \frac{1}{2}\sqrt{\frac{1}{2\sqrt{\pi}}}\ (4\cdot0^2-2) =$ 0.531125966014
第3励起状態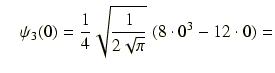： $\displaystyle \quad \psi_3(0) = \frac{1}{4}\sqrt{\frac{1}{2\sqrt{\pi}}}\ (8\cdot0^3-12\cdot0) =$ 0
第4励起状態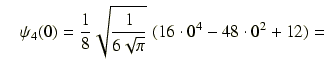： $\displaystyle \quad \psi_4(0) = \frac{1}{8}\sqrt{\frac{1}{6\sqrt{\pi}}}\ (16\cdot0^4-48\cdot0^2+12) =$ 0.459968579177

となります．したがって，規格化された波動関数の二乗の x = 0 での値は，解析解では

|ψ0(0)|2 = 0.564189583554
|ψ1(0)|2 = 0
|ψ2(0)|2 = 0.282094791774
|ψ3(0)|2 = 0
|ψ4(0)|2 = 0.211571093830

です．この値を計算値と比較してみます．

規格化された |ψ(0)|2 について，理論値，計算値，それらの差をまとめるとつぎの表のようになります．

準位理論値計算値計算値と理論値の差
n = 00.5641895835540.5641895835540.000000000000
n = 100.0000000000000.000000000000
n = 20.2820947917740.2820947917750.000000000001
n = 300.0000000000000.000000000000
n = 40.2115710938300.2115710938310.000000000001

n = 1, 3 の場合，波動関数は奇関数になるので，計算値のこの値が 0 になるのは当然です． プログラムでそのように設定していますので．比較対象になるのは n = 0, 2, 4 の場合です． 表の通り小数点第11位まで正確なようですので，なかなかの精度であるといえます．

Valid XHTML 1.1! [home] [計算物理学] [ページの先頭]

origin: 2003.12.16 / Last modified: 2004.05.24 02:51:28 JST