ダブルミニマムポテンシャルの数値解
home > 計算物理学 >[サイトマップ]
目次
ダブルミニマムポテンシャル
つぎの式で表されるポテンシャル
は相転移などを議論するとき用いられるもので,ダブルミニマムポテンシャル(二重極小ポテンシャル) もしくはダブルウェルポテンシャル(二重井戸ポテンシャル)と呼ばれるものです.プログラムのポテンシャルの形を書き換え, いくつかの a に対する固有値を求めてみました. 縦軸のスケールは各グラフによって適当に変更しています.
コーディング
アルゴリズム
微分方程式(シュレディンガー方程式)を解くのには 4 次のルンゲ・クッタ法を使います.
ソースコード
1 /* =====================================================================
2 Runge-Kutta法でダブルミニマムポテンシャルの固有値を求める
3 Last modified: May 28 2003
4 ===================================================================== */
5
6
7 #include <stdio.h>
8 #include <math.h>
9 #include "cpgplot.h"
10
11
12 // 物理設定
13 double E = 0;
14 double dE = -1.0;
15 int parity = 1;
16
17 // きざみ幅
18 double h = 0.001;
19
20
21
22 /* ---------------------------------------------------------------------
23 potential function
24 --------------------------------------------------------------------- */
25
26 double V(double x){
27 // V(x) = x^4 - ax^2
28 return (pow(x,4) - 0*pow(x,2));
29 }
30
31
32
33 /* ---------------------------------------------------------------------
34 導関数の定義
35 --------------------------------------------------------------------- */
36
37 double dphi(double x, double phi, double z){
38 // dphi/dx = z
39 return(z);
40 }
41
42 double dz(double x, double phi, double z){
43 // dz/dx = (V(x)-E)phi
44 return((V(x) - E) * phi);
45 }
46
47
48
49 /* ---------------------------------------------------------------------
50 Runge-Kutta法
51 ---------------------------------------------------------------------- */
52
53 void rungeKuttaMethod(double x0, double phi0, double z0, double h){
54 int i, j, n, loop, color;
55 double x, phi, z, k[4], q[4], phi_old[2];
56 loop = 15/h; color = 9;
57
58 for(n=1 ; n<=14 ; n++){
59 dE = -1 * dE/10;
60 x = x0; phi = phi0, z = z0; // 波動関数初期化
61
62 while(1){
63 for(i=1 ; i<=loop ; i++){
64 // 4次のRunge-kutta法 の連立
65 k[0] = h * dphi(x, phi, z);
66 q[0] = h * dz(x, phi, z);
67 k[1] = h * dphi(x + h/2, phi + k[0]/2, z + q[0]/2);
68 q[1] = h * dz(x + h/2, phi + k[0]/2, z + q[0]/2);
69 k[2] = h * dphi(x + h/2, phi + k[1]/2, z + q[1]/2);
70 q[2] = h * dz(x + h/2, phi + k[1]/2, z + q[1]/2);
71 k[3] = h * dphi(x + h, phi + k[2], z + q[2]);
72 q[3] = h * dz(x + h, phi + k[2], z + q[2]);
73 phi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
74 z += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
75 x = x0 + i * h;
76 }
77 // 今回と前回のphiを保存
78 phi_old[0] = phi_old[1]; phi_old[1] = phi;
79
80 // 今回と前回のphiが異符号ならwhile(1)を抜ける
81 // i=1ではphi_oldの値が無意味なので比較しない
82 if ( (i>=2) && ((phi_old[0] > 0) && (phi < 0)) ) break;
83 if ( (i>=2) && ((phi_old[0] < 0) && (phi > 0)) ) break;
84
85 printf("%2.15lf\n", E); // モニタ
86 E += dE; // 固有値変更
87 x = x0; phi = phi0, z = z0;
88 }
89 }
90
91 // 波動関数の描画
92 x = x0; phi = phi0, z = z0;
93 for(i=1 ; i<=loop ; i++){
94 k[0] = h * dphi(x, phi, z);
95 q[0] = h * dz(x, phi, z);
96 k[1] = h * dphi(x + h/2, phi + k[0]/2, z + q[0]/2);
97 q[1] = h * dz(x + h/2, phi + k[0]/2, z + q[0]/2);
98 k[2] = h * dphi(x + h/2, phi + k[1]/2, z + q[1]/2);
99 q[2] = h * dz(x + h/2, phi + k[1]/2, z + q[1]/2);
100 k[3] = h * dphi(x + h, phi + k[2], z + q[2]);
101 q[3] = h * dz(x + h, phi + k[2], z + q[2]);
102 cpgsci(color); cpgmove(x, phi); cpgdraw(x + h/6, phi + k[0]/6);
103 cpgsci(color); cpgmove(x + h/6, phi + k[0]/6); cpgdraw(x + h/2, phi + k[1]/2);
104 cpgsci(color); cpgmove(x + h/2, phi + k[1]/2); cpgdraw(x + h*5/6, phi + k[2]*5/6);
105 cpgsci(color); cpgmove(x + h*5/6, phi + k[2]*5/6); cpgdraw(x + h, phi + k[3]);
106 phi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
107 z += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
108 x = x0 + i * h;
109 }
110
111 // 求まった固有値を表示
112 printf("E = %2.15lf\n", E);
113 }
114
115
116
117 /* ---------------------------------------------------------------------
118 ポテンシャルの形を描画
119 --------------------------------------------------------------------- */
120
121 void drawPotential(double xmax)
122 {
123 double i;
124 cpgsci(4); cpgslw(1);
125 cpgmove(-xmax, pow(xmax,2)/2);
126 for(i = -xmax ; i < xmax ; i += 0.1){
127 cpgdraw(i, pow(i,4) - 0*pow(i,2));
128 }
129 }
130
131
132
133 /* ---------------------------------------------------------------------
134 main
135 --------------------------------------------------------------------- */
136 int main(void)
137 {
138 double phi0, z0;
139 double xmax, bottom, top;
140
141 // グラフ描画設定
142 xmax = 4.0;
143 bottom = 1.3;
144 top = 1.3;
145 cpgopen( "/xserv" );
146 cpgpap( 7.0, .6 );
147 cpgenv( 0, xmax, -bottom, top, 0, 0 );
148
149 if (parity == -1) {
150 phi0 = 0.0; z0 = 1.0; // 奇関数
151 }
152 else {
153 phi0 = 1.0; z0 = 0.0; // 偶関数
154 }
155
156 drawPotential(xmax);
157 rungeKuttaMethod(0., phi0, z0, h);
158
159 cpgclos();
160 return 0;
161 }
実行結果
ダブルミニマムポテンシャル V(x) = x4 - a x2 の a の値を変えて,いくつかのポテンシャルで計算してみました.
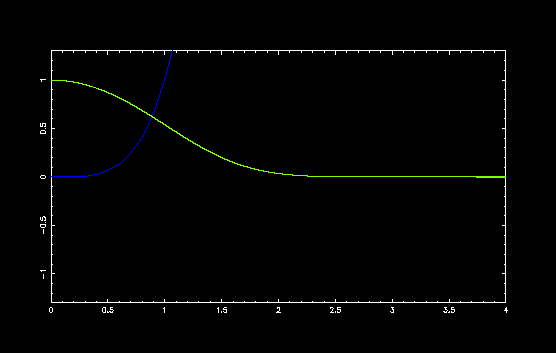
a = 0, E = 1.060362090484170
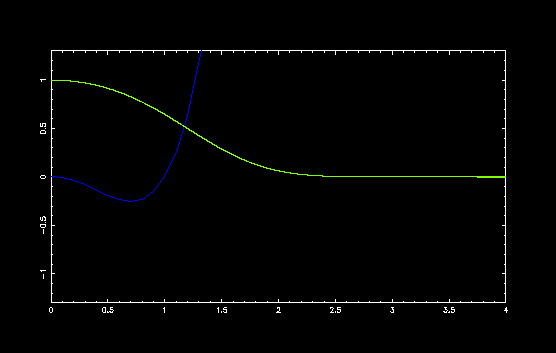
a = 1, E = 0.657653005180699
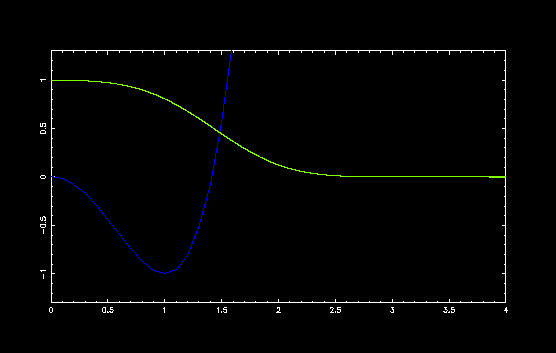
a = 2, E = 0.137785848188210
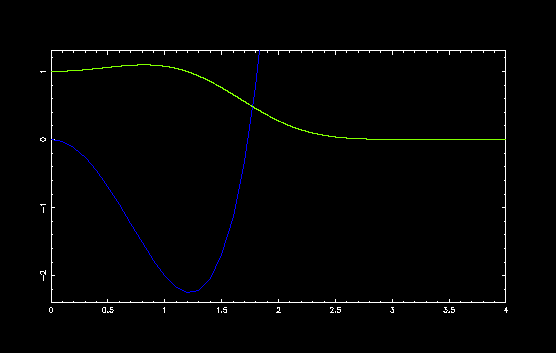
a = 3, E = -0.593493304218450
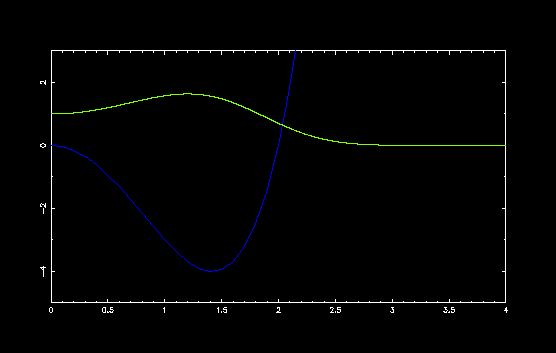
a = 4, E = -1.710350450132565
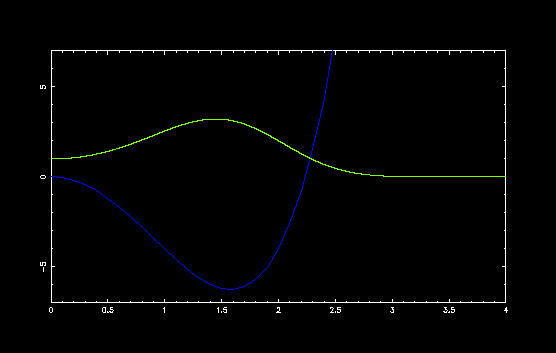
a = 5, E = -3.410142761239649
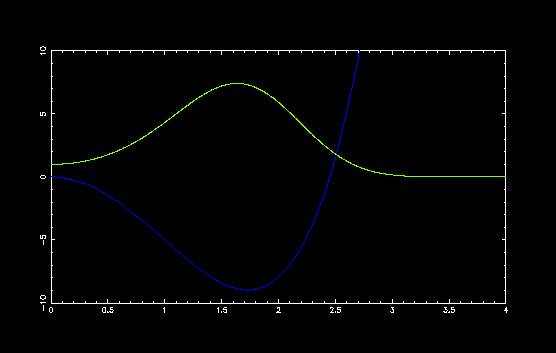
a = 6, E = -5.748190520666807
x = 0 でポテンシャルの山が高くなるにしたがって, 固有値と固有関数が変化する様子がわかります. 中央のポテンシャルの山が高いと古典的には粒子は一方の谷の中央で振動しますから, 量子力学的にも山が高い場合には,それぞれの谷で振動している2つの振動子を考えることができます.