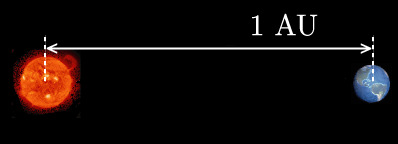天文単位(AU)を測る
ここでは天文単位(AU)の測り方について書いています.ケプラーの第三法則の応用です.
天文単位の測定
さて,天文単位が「太陽と地球の間の距離」を表すことはわかりました. 理科年表から具体的な数字をもってきてみましょう.
Important
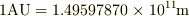
太陽と地球の間の距離が数km の精度で決まっているなんてびっくりです. [*] いったいどうやって求められているのでしょうか?
| [*] | ちなみに最新の論文ではさらに有効数字が多くて 数十m の精度になっています. |
ガウスによる定義
太陽と地球の間の平均距離が上に書いたような精度で求まるのでしょうか? 求まるとしたらどうやって求めているのでしょうか?
1 天文単位は最初 C.F.Gauss さんによって地球-太陽間の平均距離,より正確には地球の軌道長半径として定義されました.
軌道長半径は ケプラーの第三法則 を使って求めることができます. ケプラーの第三法則は次のようなものでした.
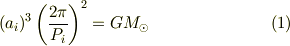
ここで 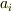 は太陽系
は太陽系 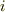 番目の惑星の軌道長半径,
番目の惑星の軌道長半径, 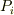 は
は 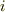 番目の惑星の軌道周期です.
番目の惑星の軌道周期です.
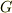 は重力定数で,
は重力定数で, 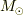 は太陽質量を表します.
は太陽質量を表します.
いま,求めたいのは地球-太陽間の距離ですから 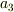 の値です.
の値です.
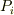 は直接測定することができます(地球の軌道周期は 365日 ですよね!).
太陽質量
は直接測定することができます(地球の軌道周期は 365日 ですよね!).
太陽質量 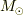 は直接求めることができないのでこれも未知数となります.
は直接求めることができないのでこれも未知数となります.
測定するぞ
さて,ところでレーダー技術の発達により地球と他の惑星(金星や火星)との間の距離はかなり正確に求められるようになっています. ここでは金星までの距離がかなり正確にわかるものとして話を進めましょう.
レーダー技術は大雑把に言うと,地球から金星に向けて光を発して,金星で反射した光を地球で再び受けとるというものです. [†]
地球から金星に向けて光を発して,反射して帰ってくるまでの時間を 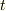 とします.
これを測定するわけです.
とします.
これを測定するわけです.
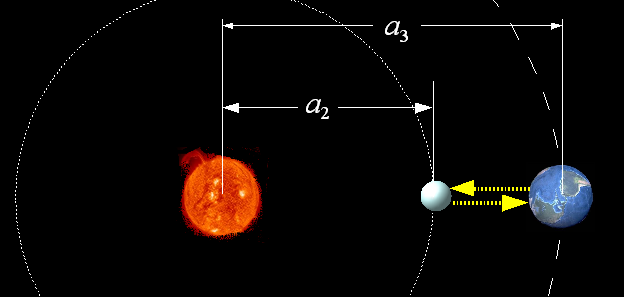
図2. レーダーによる地球と金星の間の距離測定(概念図)
光の速さ,つまり光速  は一定値をとることが知られているので,金星-地球間の軌道長半径の差は,金星-太陽間の距離が
は一定値をとることが知られているので,金星-地球間の軌道長半径の差は,金星-太陽間の距離が 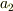 ですから次のように表すことができます.
ですから次のように表すことができます.

ここで 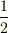 という係数がつくのは
という係数がつくのは 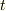 が往復の時間を計っているからです.
が往復の時間を計っているからです.
式(1)から,地球・金星のそれぞれについてケプラーの第三法則を適用して
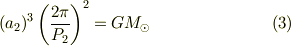
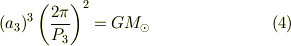
が成り立ちます.
さて,式(2), (3), (4) で式が三本,未知数は 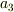 ,
, 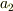 ,
, 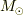 の3つですから,未知数を決定することができますね.
式(3)と(4)を連立すると,次式が得られます.
の3つですから,未知数を決定することができますね.
式(3)と(4)を連立すると,次式が得られます.
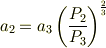
これを式(2)に代入すると,
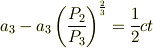
となり,これを 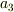 について整理してやると
について整理してやると
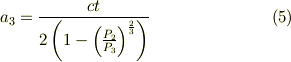
となり,求めたかった 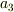 がすべて測定可能な量で表すことができました.ヽ(´ー`)ノ
がすべて測定可能な量で表すことができました.ヽ(´ー`)ノ
実際の値を代入しよう
式(5) に実際の値を代入してみることにしましょう. その前に次の図を見てみてください.
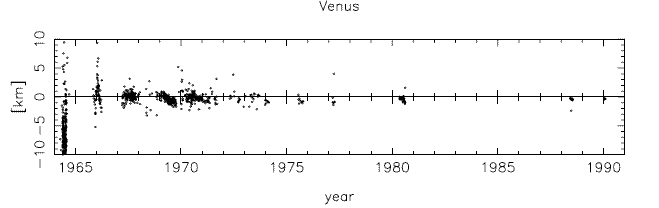
E.M.Standish, Proceedings of the International Astronomical Union (2005), 2004: 163-179 Cambridge University Press
これは上の方法で地球と金星の間の距離を測定したときの誤差の大きさを年代ごとにプロットしたものです.
1960年代の測定では誤差が 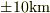 ほどありますが,最近ではもう
ほどありますが,最近ではもう 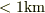 の精度になっています.
これならば最初にあげた精度を達成できそうですね.
の精度になっています.
これならば最初にあげた精度を達成できそうですね.
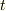 は観測データが公開されています.一部をお見せしましょう. [‡]
は観測データが公開されています.一部をお見せしましょう. [‡]
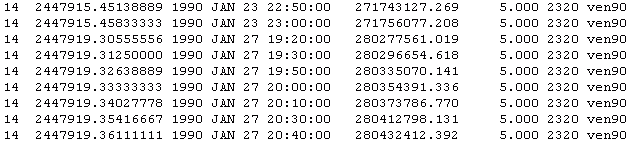
左から 7 列目に,光が往復するのにかかった時間がミリ秒単位で書かれています. 8 列目にその誤差がやはりミリ秒単位で書かれています.
これくらいの精度で計れるならば,地球-金星間の距離が 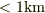 の精度で測れるのも納得ですね.
の精度で測れるのも納得ですね.
よし,代入だ.
では実際に観測されている値を (5) に代入してみましょう.
理科年表によれば 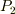 は
は 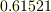 太陽年,
太陽年, 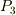 は
は 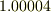 太陽年です.
ここでは
太陽年です.
ここでは 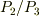 の比が欲しいだけなので単位は太陽年のままでいいでしょう.
の比が欲しいだけなので単位は太陽年のままでいいでしょう.
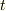 については先ほどのデータから得られますが,地球と金星の位置関係が 図2 のようになっているとは限らないのでそのまま使うことはできません.
位置関係を考慮した補正が必要です.
補正は非常に複雑なのでここではそれをやらずに次のような近似を行いましょう.
地球と金星の軌道をともに円軌道と仮定するとお互いが半径の差よりも近づくことはないので, データ の一番小さな往復時間を
については先ほどのデータから得られますが,地球と金星の位置関係が 図2 のようになっているとは限らないのでそのまま使うことはできません.
位置関係を考慮した補正が必要です.
補正は非常に複雑なのでここではそれをやらずに次のような近似を行いましょう.
地球と金星の軌道をともに円軌道と仮定するとお互いが半径の差よりも近づくことはないので, データ の一番小さな往復時間を 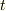 として採用することにします.
データ で一番小さな値は
として採用することにします.
データ で一番小さな値は 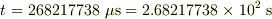 ですのでこれを使いましょう.
ですのでこれを使いましょう.
光速  は
は 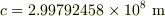 です.
です.
これらを代入すると 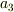 の値はだいたい
の値はだいたい
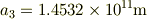
となります.大雑把な近似のせいで理科年表に書かれている値からは少し外れていますが,天文単位を求めることができました. :)
| [†] | ここでいう光は目に見える「可視光」ではなくて「電波」という波長の光になります. |
| [‡] | 全部を見たい場合は NASA JPL のここ に公開されています. |
問い
上では太陽-地球間の軌道長半径を求めましたが,その結果を使えば 式(4) から太陽質量 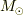 を求めることができます.求めてください.
ただし今回はより精確な理科年表の値を使うことにしましょう.
その際に有効数字がどうなるかも,注意してください.
を求めることができます.求めてください.
ただし今回はより精確な理科年表の値を使うことにしましょう.
その際に有効数字がどうなるかも,注意してください.
IAU 1976 の定義
実は,現在では天文単位(AU)は太陽-地球間の距離というようには定められていません. 国際天文学連合(IAU)によって,1976年に形式的に次のように定められました.
Important
質量を持たない粒子が太陽のまわりを完全な円軌道で 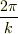 日 (365.2568983...日) の周期をもってまわるような半径を 1 天文単位と定める.
ここで
日 (365.2568983...日) の周期をもってまわるような半径を 1 天文単位と定める.
ここで 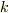 はガウス定数と呼ばれるもので,厳密に 0.01720209895 という値をもつ.
はガウス定数と呼ばれるもので,厳密に 0.01720209895 という値をもつ.