ラグランジュの運動方程式を確認しよう!
目的と方針
ラグランジュの運動方程式は,いろんな座標で成り立つから便利だけど自力で導くのが難しくて, 使ってて気持ち悪いなあとか,思うことってありませんか? ラグランジュの運動方程式を導出する方法のひとつに,ダランベールの原理から出発して直交座標の式から 一般座標の式に持っていくという方法があります.でも,計算量も案外多くて,先が見えにくいから, 自力で最後までたどり着くのは結構大変ですよね. そこで,変分法 [*] を用いて自力でラグランジュの運動方程式を導けるようになることを目標にがんばって みましょう!
次の方針で示すことにします.前提として,デカルト座標ではラグランジュの運動方程式が 成立するということは,認めることにしましょう [†] .そこで,変分法を使って一般にどの 座標で運動を表してもデカルト座標で表したことと同値なんだよ,ということを示すことにします. そうすれば,どの座標系でもラグランジュの運動方程式が成り立つことが示せたことになりますね.
では,早速やってみましょう!
[*] この記事では,変分法について細かい内容は扱いません.変分法をはじめて学ぶ方は, 変分法1 を参照ください.
[†] デカルト座標だと成り立つの?っていう人は, ラグランジュの運動方程式 をご覧ください.
変分法を使う準備
できるだけ一般的な運動を扱って行くことにしましょう.考える質点系の自由度を 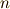 とし,これらの質点系
が時刻
とし,これらの質点系
が時刻 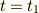 から時刻
から時刻 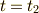 の間にどのような運動をするかを考えます.
このとき,粒子の運動は
の間にどのような運動をするかを考えます.
このとき,粒子の運動は 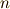 個の変数で記述できるので,それらの変数をを
個の変数で記述できるので,それらの変数をを 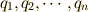 とおき,
運動の出発点と終着点は決めてしまいます.この2点を結ぶ任意の曲線を
とおき,
運動の出発点と終着点は決めてしまいます.この2点を結ぶ任意の曲線を 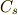 と表現します.
この力学系を表すラグランジアンを
と表現します.
この力学系を表すラグランジアンを 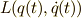 もしくは単に
もしくは単に 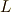 と表すことにしましょう.
と表すことにしましょう.
天下り的になりますが,作用と呼ばれる量 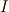 を次のように定めます.
を次のように定めます.
![I[C_s] = \int_{t_1}^{t_2} L(q(t,C_s),\dot{q}(t,C_s)) \mathrm{d} t \tag{1}](./df7fefe377e2d05b21ac65c5527e8999.png)
作用 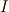 が極値や鞍点などの停留点をとる条件(すなわち
が極値や鞍点などの停留点をとる条件(すなわち 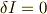 )を考えれば,目標のラグランジュの方程式に
たどり着くことができます.
)を考えれば,目標のラグランジュの方程式に
たどり着くことができます.
この作用 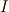 は,一体なんだ?と思うかもしれませんが,ここでは目標を達成するためにこういうものを
考えてみただけと割り切って,先に進んでみましょう. [‡]
は,一体なんだ?と思うかもしれませんが,ここでは目標を達成するためにこういうものを
考えてみただけと割り切って,先に進んでみましょう. [‡]
[‡] この背後には,''実際にその運動が起こるとき,作用 が停留点をとる''という,変分原理の考え方が実は隠れています.しかし,ここでの目的はデカルト座標によるラグランジュの運動方程式の表現と一般化座標によるラグランジュの運動方程式が同値であることを示したいだけなので,今は数学的なわざとして受け入れることにします.
ラグランジュの運動方程式
ここでは,質点系はポテンシャルによる力のみを受けて運動している場合を考えます. [§]
上のセクションで作用 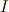 を導入しました.
を導入しました. 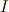 が停留点を取る経路が
が停留点を取る経路が 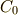 であるとします.
さて,では経路を微小量だけずらしてみたらどうでしょう.このときの経路を
であるとします.
さて,では経路を微小量だけずらしてみたらどうでしょう.このときの経路を 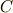 とします.
このとき,実際の運動からの座標のずれを一般に
とします.
このとき,実際の運動からの座標のずれを一般に  と表すことにし,出発点
と終着点は分かっているから,そこでのずれはないものとしましょう.
と表すことにし,出発点
と終着点は分かっているから,そこでのずれはないものとしましょう.
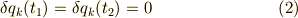
このずれのことを変分と呼び,十分に小さいものとして扱います.
さて, ![I[C]](./34c3ce41f731789c5cac05b444805a03.png) の
の ![I[C_0]](./ae1b7a3edf451d5b6c549d19e2f639a8.png) からのずれを
からのずれを  として,次のように表されます.
として,次のように表されます.
![\delta I &\equiv I[C]-I[C_0] \\&=\int_{t_1}^{t_2} \left(L(q+\delta q,\dot{q}+\delta \dot{q})-L(q,\dot{q})\right) \mathrm{d}t \tag{3}](./518a46ad34056ae162a60e262128a742.png)
ここで,  が十分に小さいので,
が十分に小さいので,  を展開し,微小量の2次以上の項を無視すれば,次式を得ます.
を展開し,微小量の2次以上の項を無視すれば,次式を得ます.
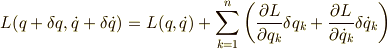
よって, 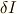 は次式で表せます.
は次式で表せます.
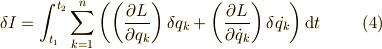
経路変更による変分 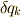 と実際に運動したことによる変位
と実際に運動したことによる変位 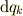 は互いに無関係ですから,
は互いに無関係ですから,

が成り立ちます. つまり,式(4)の右辺第2項は部分積分を用いて次のように変形できます.
![\int_{t_1}^{t_2}\sum_{k=1}^{n}\left( \frac{\partial L}{\partial \dot{q}_k}\right) \delta \dot{q_k}\mathrm{d}t = \left[ \sum_{k=1}^{n}\left(\frac{\partial L}{\partial \dot{q}_k}\right)\delta q_k \right]_{t_1}^{t_2} - \int_{t_1}^{t_2}\sum_{k=1}^{n}\left(\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{q}_k}\right)\delta q_k\mathrm{d}t \tag{6}](./5532b7dcedd32f888f479582ed2efacf.png)
右辺第1項は,境界条件の式(2)によって  となりますから,式(4)は次のようにまとめることができます.
となりますから,式(4)は次のようにまとめることができます.
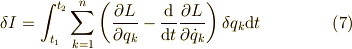
ここで,停留点をとる条件は,上式が  になることですが,変分はすべて独立でしたから,
になることですが,変分はすべて独立でしたから, 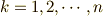 について
について
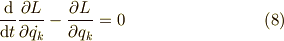
となります.やっと,ラグランジュの方程式が出てきました.^^
ここで大事なのは,運動を表す変数の種類を特に指定していないことです.つまり,運動を記述できる変数なら何でもよかった わけで,そこには当然デカルト座標も含まれます.デカルト座標でなら,ラグランジュの運動方程式とニュートンの運動方程式 が同じであることは容易に示せますから,結局ラグランジュの運動方程式は任意の座標系で成り立つことが示せたわけです.
変分法を使うと,ずいぶんあっさり示すことができてしまいましたね.変分法に慣れるまでは大変かもしれませんが, 一度身に着けてしまうと解析力学に見通しがずいぶんよくなること間違いなしですから,しっかり身に着けてくださいね.
[§] ポテンシャル以外からの力を受けていても,ほぼ同様の手順で示すことができますが,簡単のためここでは扱いませんでした.詳しくは 変分原理 で扱う予定ですから,しばらくお待ちください.