共役な物理量とポアソン括弧
この記事では,通常
![\left[ A , B \right] = \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial p} - \dfrac{\partial A}{\partial p} \dfrac{\partial B}{\partial q}\tag{1}](./ad96f188ab0db9042c9626abbcfb50a9.png)
で定義されるポアソン括弧について考えることで,共役な変数とは何か?を考えます.
古典力学です.解析力学では一般的な共役な物理量と言うと, 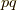 等の様に,積の次元がエネルギー×時間の次元を持つと言う定義です.
等の様に,積の次元がエネルギー×時間の次元を持つと言う定義です.
復習(q,pに対するポアソン括弧)
まずは, 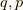 を基にしたポアソン括弧を区別する為,
を基にしたポアソン括弧を区別する為,
![\left[ A , B \right]_{q,p} \equiv \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial p} - \dfrac{\partial A}{\partial p} \dfrac{\partial B}{\partial q}\tag{2}](./bdddfb0b7204c59ee3d5460b3cfe115c.png)
と書くことにします.ある物理量  と変数
と変数  or
or 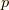 のどちらか単独でポアソン括弧に入れると,それは正負の符号を無視すれば,共役な変数での微分をした事になるのでした.
のどちらか単独でポアソン括弧に入れると,それは正負の符号を無視すれば,共役な変数での微分をした事になるのでした.
![\left[ q , X \right]_{q,p} &= \dfrac{\partial q}{\partial q} \dfrac{\partial X}{\partial p} - \dfrac{\partial q}{\partial p} \dfrac{\partial X}{\partial q} = \dfrac{\partial X}{\partial p}\tag{3}](./6b355df0e8d81b3019e207043c4fc9d8.png)
![\left[ p , X \right]_{q,p} &= \dfrac{\partial p}{\partial q} \dfrac{\partial X}{\partial p} - \dfrac{\partial p}{\partial p} \dfrac{\partial X}{\partial q} = - \dfrac{\partial X}{\partial q}\tag{4}](./b8a1388910782eb06a4cf41ac6ac95e1.png)
実験(t,Eに対するポアソン括弧)
ここで,共役な変数として有名な時間  とエネルギー
とエネルギー 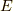 を
を 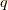 と
と 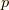 の代わりに使ってみたらどうなるでしょう?自由粒子の時
の代わりに使ってみたらどうなるでしょう?自由粒子の時 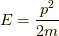 として,
として, ![\left[ q , E \right]_{t,E}](./1d5e25be0756ab7c19fd6bd6ceece5cc.png) を計算すると,
を計算すると, 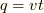 ,
, 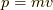 ですから,
ですから,
![\left[ q , E \right]_{t,E} &= \dfrac{\partial q}{\partial t} \dfrac{\partial E}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial E}{\partial t} \\&= \dfrac{\partial (vt)}{\partial t} \dfrac{\partial E}{\partial E} - \dfrac{\partial (vt)}{\partial E} \dfrac{\partial E}{\partial t} \\&= v \cdot 1 - 0 \\&= \dfrac{p}{m} \\&= \dfrac{\partial \dfrac{p^2}{2m}}{\partial p} \\&= \left[ q , E \right]_{q,p}\tag{5}](./54e3ba86495a5c87aae102f7920c3c6d.png)
おや,これは偶然でしょうか?
調和振動子の時( 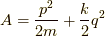 )もやってみましょう.もう一つを
)もやってみましょう.もう一つを 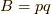 にしてみます.この
解の一つは,
にしてみます.この
解の一つは, 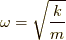 として,
として, 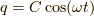 ,
, 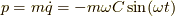 です.
です.
![\left[ \dfrac{p^2}{2m} + \dfrac{k}{2}q^2 , pq \right]_{q,p} &= \dfrac{\partial (p^2/2m + kq^2/2)}{\partial q} \dfrac{\partial (pq)}{\partial p} - \dfrac{\partial (p^2/2m + kq^2/2)}{\partial p} \dfrac{\partial (pq)}{\partial q} \\&= kq \cdot q - \dfrac{p}{m} \cdot p \\&= -\dfrac{p^2}{m} + kq^2 \\&= -m \omega^2 C^2 \sin^2 (\omega t) + k C^2 \cos (\omega t) \\&= k C^2 \cos (2 \omega t)\tag{6}](./20a460fba42194e9f8492abfccd6dcb2.png)
です.一方, 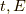 のポアソン括弧は(
のポアソン括弧は( 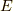 は運動の定数なので
は運動の定数なので 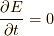 ),
),
![\left[ \dfrac{p^2}{2m} + \dfrac{k}{2}q^2 , pq \right]_{t,E} &= \dfrac{\partial E}{\partial t} \dfrac{\partial (pq)}{\partial E} - \dfrac{\partial E}{\partial E} \dfrac{\partial (pq)}{\partial t} \\&= 0 \cdot ? - 1 \cdot \dfrac{\partial (-m \omega C^2 \sin \omega t \cos \omega t)}{\partial t} \\&= \dfrac{\partial (\dfrac{m}{2} \omega C^2 \sin 2 \omega t)}{\partial t} \\&= m \omega^2 C^2 \cos (2 \omega t) \\&= k C^2 \cos (2 \omega t) \\&= \left[ \dfrac{p^2}{2m} + \dfrac{k}{2}q^2 , pq \right]_{q,p}\tag{7}](./b4d9973e85a9088912870f5dc6854f34.png)
なるほど,一致しましたね.これは偶然ではなさそうです.
q,pの括弧とt,Eの括弧が同じ値を取ることの証明
個々の例に囚われていてはいけません.ある程度一般化して考えましょう.
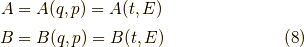
と置いて計算してみましょう!
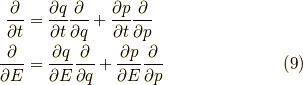
ポアソン括弧 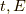 を計算すると,
を計算すると,
![\left[ A, B \right]_{t,E} &= \dfrac{\partial A}{\partial t} \dfrac{\partial B}{\partial E} + \dfrac{\partial A}{\partial E} \dfrac{\partial B}{\partial t} \\&= \left( \dfrac{\partial A}{\partial q} \dfrac{\partial q}{\partial t} + \dfrac{\partial A}{\partial p} \dfrac{\partial p}{\partial t} \right) \cdot \left( \dfrac{\partial B}{\partial q} \dfrac{\partial q}{\partial E} + \dfrac{\partial B}{\partial p} \dfrac{\partial p}{\partial E} \right) \\&- \left( \dfrac{\partial A}{\partial q} \dfrac{\partial q}{\partial E} + \dfrac{\partial A}{\partial p} \dfrac{\partial p}{\partial E} \right) \cdot \left( \dfrac{\partial B}{\partial q} \dfrac{\partial q}{\partial t} + \dfrac{\partial B}{\partial p} \dfrac{\partial p}{\partial t} \right) \\&= \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial q} \left(\dfrac{\partial q}{\partial t} \dfrac{\partial q}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial q}{\partial t} \right) \\&+ \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial p} \left(\dfrac{\partial q}{\partial t} \dfrac{\partial p}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial p}{\partial t} \right) \\&- \dfrac{\partial A}{\partial p} \dfrac{\partial B}{\partial q} \left(\dfrac{\partial q}{\partial t} \dfrac{\partial p}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial p}{\partial t} \right) \\&+ \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial p} \left(\dfrac{\partial p}{\partial t} \dfrac{\partial p}{\partial E} - \dfrac{\partial p}{\partial E} \dfrac{\partial p}{\partial t} \right) \\&= \left( \dfrac{\partial A}{\partial q} \dfrac{\partial B}{\partial p} - \dfrac{\partial A}{\partial p} \dfrac{\partial B}{\partial q} \right) \cdot \left(\dfrac{\partial q}{\partial t} \dfrac{\partial p}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial p}{\partial t} \right) \\&= \left[ A, B \right]_{q,p} \cdot \left[ q, p \right]_{t,E} \tag{10}](./0e83b5fb8abaca3104f5cfc6343853a4.png)
よって,
![\left[ A, B \right]_{t,E} = \left[ A, B \right]_{q,p} \tag{11}](./bb4806eafe4f16d05adb03bf91cedccd.png)
を満たすには,
![\left[ q, p \right]_{t,E} = 1 \tag{12}](./53f6fcc801d4ec813a67384c48ff8f64.png)
が成立していなければなりません.
最後の仕上げ
![\left[ q, p \right]_{t,E} = 1 \tag{13}](./5b6b13329a28475967717ec1faab8509.png)
を示します.今,ハミルトニアンは 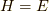 とします.記号こそ違うものの同じエネルギーを表しています.
一応,
とします.記号こそ違うものの同じエネルギーを表しています.
一応, 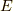 の
の  依存性を考慮しておくと,
依存性を考慮しておくと,
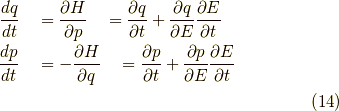
より,
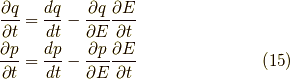
ですから,
![\left[ q, p \right]_{t,E}&= \dfrac{\partial q}{\partial t} \dfrac{\partial p}{\partial E} - \dfrac{\partial q}{\partial E} \dfrac{\partial p}{\partial t} \\&= \left( \dfrac{dq}{dt} - \dfrac{\partial q}{\partial E} \dfrac{\partial E}{\partial t} \right) \dfrac{\partial p}{\partial E} - \left( \dfrac{dp}{dt} - \dfrac{\partial p}{\partial E} \dfrac{\partial E}{\partial t} \right) \dfrac{\partial q}{\partial E} \\&= \dfrac{dq}{dt} \dfrac{\partial p}{\partial E} - \dfrac{dp}{dt} \dfrac{\partial q}{\partial E} \\&= \dfrac{\partial H }{\partial p} \dfrac{\partial p}{\partial E} + \dfrac{\partial H }{\partial q} \dfrac{\partial q}{\partial E} \\&= \dfrac{\partial H }{\partial E} \\&= 1 \ \ \ (\because H=E)\tag{16}](./0ec4b4a38c2d9528726e52c8beece431.png)
ふう,証明できました.ここで,共役な変数とは,最初に一対 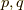 を共役と決めたら,確かめたい変数
を共役と決めたら,確かめたい変数 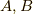 として,そのポアソン括弧
として,そのポアソン括弧 ![\left[ A,B \right]_{q,p}](./82379e135f3d8fefdbe9d04869d89cbf.png) ,もしくは,
,もしくは, ![\left[ q,p \right]_{A,B}](./a3cf984091ece5cc086c1ec8e5e12f06.png) が1に等しくなるような変数の組と言えそうです.逆に1に等しい時,それらの変数は共役であるかどうかは分かりませんでした.
が1に等しくなるような変数の組と言えそうです.逆に1に等しい時,それらの変数は共役であるかどうかは分かりませんでした.
ちなみに,僕が気になっていることを話しておくと,電荷 ![Q[C]](./8c6909e20337d34941210c99d5e3a69e.png) と磁荷
と磁荷 ![Q_m[Wb]](./b81da644cee33fe00f0cec2b67c690aa.png) の積は,
の積は,  から確かめると,なんと
から確かめると,なんと ![[C][Wb]=[J \cdot s]](./b1be2f4ff4c110f140ca47f26bf2fe86.png) で(少なくとも)次元については共役かもしれないということが言えます.実際に,
で(少なくとも)次元については共役かもしれないということが言えます.実際に, ![[Q,Q_m]_{q,p}=1](./6ee9cdcbd5e1c373f0d052b082a2d549.png) になるかどうかは分かりません.そもそもこんな計算は現実に対応する物理的な量ではないかもしれませんが,興味の一つに持っておこうと思います.
になるかどうかは分かりません.そもそもこんな計算は現実に対応する物理的な量ではないかもしれませんが,興味の一つに持っておこうと思います.
今日はここまで,お疲れさまでした!