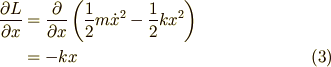調和振動子とラグランジュの運動方程式

ラグランジュの運動方程式の簡単な適用例として，調和振動子の運動を考えてみます．

調和振動子

バネに取り付けられたおもりが振動するような運動を，調和振動子といいます．自然界にはこのような運動が多くみられるため，物理の問題でも調和振動子が多く登場しています．ここでラグランジュの運動方程式を考えるのは，つぎの図のような，水平面上の調和振動子です．

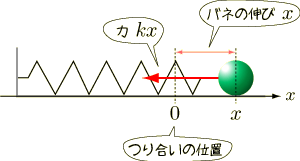
図のように座標軸等を取り，おもりの質量を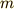とします．ニュートンの運動方程式はすぐに分かって，

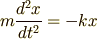
$m\frac{d^2x}{dt^2}= -kx$

となります．このあらかじめ分かっている方程式をわざわざラグランジュの方程式から導いてみる，ということをします．

ラグランジアン

ラグランジアンを書き出します．解析力学のお偉いさん，ラグランジアン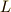とは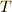，を運動エネルギー，をポテンシャルエネルギーとして

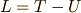
なる量のことでした．ティーまいなすユーです．いまは単純な調和振動子の運動を考えていますから，運動エネルギー，ポテンシャルエネルギーはすぐに分かって

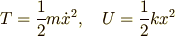
$T = \frac{1}{2}m\dot{x}^2, \quad U=\frac{1}{2}kx^2$

と書けます．ここで $\dot{x}$ とはの時間微分，すなわち速度のことです．したがってラグランジアン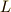は

$L = T-U = \frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2$

となります．位置と，その時間微分 $\dot{x}$ は，独立した変数として取り扱うことに注意しておきます．

ラグランジュの運動方程式

さて，ラグランジアンが分かったので，いよいよラグランジュの運動方程式を考えましょう．ラグランジュの運動方程式は

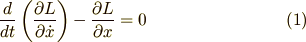
$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} = 0 \tag{1}$

というものでしたから，さきほどのラグランジアンをこの方程式に代入して計算します．計算すると，ニュートンの運動方程式と同じ形になるはずです．いっぺんにやると難しそうなので，左側第1項から順々に計算してみます．

第1項を計算

ラグランジアンを $\dot{x}$ で偏微分します．の項は消えます．さらにそれを時間微分します．

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) &= \frac{d}{dt}\left\{ \frac{\partial}{\partial \dot{x}} \left(\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2\right) \right\}\\ &= \frac{d}{dt}(m\dot{x}-0)\\ &= m\ddot{x} \tag{2}$

第2項を計算

ラグランジアンをで偏微分します． $\dot{x}$ の項は消えます．

$\frac{\partial L}{\partial x} &= \frac{\partial}{\partial x} \left(\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2\right)\\ &= -kx \tag{3}$

ラグランジュの運動方程式を計算

各項が計算できたので，ラグランジュの方程式

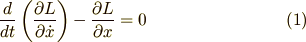
$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} = 0 \tag{1}$

を整理します．式(1)に式(2)，(3)を代入すると

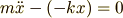
$m\ddot{x}-(-kx) = 0$

となります．移項して

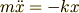
$m\ddot{x} = -kx$

であり，さらに 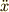$\ddot{x}$ を微分の形で表すと

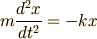
$m\frac{d^2x}{dt^2} = -kx$

です．これは，最初にみたニュートンの運動方程式です．今回は，1次元の調和振動子を例にとってラグランジュの運動方程式のアプローチを練習してみました．しかしこれだけでは，計算が繁雑になっただけでなんのメリットもありません．つぎはこれと同様のアプローチで，ニュートンの運動方程式を直接記述するのが難しい，極座標の運動を記述してみましょう．

[home] [解析力学] [ページの先頭]