エネルギーの定義とエネルギー保存則
エネルギー保存則について考えてみましょう.そもそも,僕たちは解析力学のなかでエネルギーを定義していませんでした. エネルギーはニュートン力学で重要な概念でしたから,これをほっておくわけにもいきません. (そもそもラグランジアンは,単純な力学系では運動エネルギーとポテンシャルエネルギーで記述されていたではありませんか! 解析力学にエネルギーの概念は必要不可欠なのです.)
そこで,この記事ではエネルギーの定義と保存則について考えてみようと思います.
エネルギー
さて,エネルギーを定義するといっても,どのように定義したらよいのでしょう?エネルギーを表す関数を 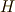 とおいて,
ニュートン力学のときとの類推から
とおいて,
ニュートン力学のときとの類推から 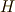 として次の条件を満たすものを考えましょう.
として次の条件を満たすものを考えましょう.
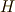 の単位はSI単位系で
の単位はSI単位系で ![[m^2kgs^{-2}]](./85a651734963c25345c701fc4686336a.png) となる.
となる.- 非保存力が存在しない時には保存則が成立する.
- 単純な力学系においてラグランジアンが
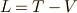 と書けるとき
と書けるとき 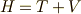 と表せる.
と表せる.
こんな量 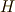 をどうやって探していきましょうか?保存則が成立するということは,ネーターの定理が成立している
可能性がありますね. [*]
さらに,
をどうやって探していきましょうか?保存則が成立するということは,ネーターの定理が成立している
可能性がありますね. [*]
さらに, 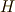 の次元が定まってますから,まずは次元解析をやってみましょう.
の次元が定まってますから,まずは次元解析をやってみましょう.
| [*] | ここで少し注意を喚起しておきます.一般に作用(もしくはラグランジアン)に対称性が存在すれば,保存則が成立することは保証されますが,その逆は必ずしも成立するわけではありません(つまり,保存則が成立するからといって作用やラグランジアンに対称性があるとは限りません).ここでは,ネーターの定理が成立しているのではないかと予想して,議論してみます. |
次元解析
次元解析は複数の物理量の間に成立する未知の関係式を求めるときに,ヒントを与えてくれることが良くあります.
ここでは,保存則の成立という観点からエネルギー 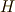 に関する ネーターの定理 を探ってみましょう.
に関する ネーターの定理 を探ってみましょう.
一般化運動量の保存則では,作用積分の変分が以下の式で表せましたね.
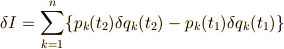
つまり,作用  の第1変分が(物理量
の第1変分が(物理量  座標の微小変化)と書けるときに,
座標の微小変化)と書けるときに,  が成立すれば
保存則が得られる,ということでした.
が成立すれば
保存則が得られる,ということでした.
ここで,作用  の単位は定義より,SI単位系で
の単位は定義より,SI単位系で ![[m^2kgs^{-1}]](./2814a5ca4a2c1fe7e7553262b6405588.png) となります.つまり,その次元はエネルギーに
時間をかけたものと言うことができるでしょう.この結果から,エネルギーの保存則を得るために動かすべき変数は
位置を表す座標ではなく時間ではないか,と想像されます.
となります.つまり,その次元はエネルギーに
時間をかけたものと言うことができるでしょう.この結果から,エネルギーの保存則を得るために動かすべき変数は
位置を表す座標ではなく時間ではないか,と想像されます.
これまで,作用積分の変分を考えるときは座標のみの変分を考えてきました.しかし,今度は調べる運動の時間を 微小にずらすことを考えていきましょう.
エネルギーの定義と保存則
今までと同じ質点系の運動を考えていきます.すなわち,自由度 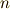 で時刻
で時刻 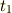 から
から 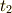 の間に質点系がする運動
を考えます.このとき,作用
の間に質点系がする運動
を考えます.このとき,作用 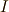 はラグランジアン
はラグランジアン 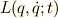 を用いて
を用いて
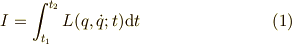
と表せます.保存則を得るための変分を考えるのですから ネーターの定理 を得たときと同じようにラグランジュの運動方程式
は分かっているものとしましょう.前のセクションでやった考察より,今度は運動の初めと終わりを表す位置座標の変化は
ないものとして,運動を考える時刻を  から
から 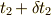 に変化させます.このときの変分
に変化させます.このときの変分 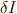 は
次式で定義されます.
は
次式で定義されます.
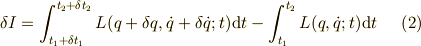
ここで, 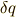 や
や  は,時間の微小変化に伴って考えなくてはならない座標の微小変化です.
どういうことかというと,本来質点系に何の変化も加えず時間を微小にずらせば,質点は微小量だけ動くはずです.
しかし,時間をずらしても運動の初めと終わりの位置座標はずらさないという条件を考えることにしました.その条件を
満たすためには,座標や速度を微小量だけずらさなくてはならないということになります.
は,時間の微小変化に伴って考えなくてはならない座標の微小変化です.
どういうことかというと,本来質点系に何の変化も加えず時間を微小にずらせば,質点は微小量だけ動くはずです.
しかし,時間をずらしても運動の初めと終わりの位置座標はずらさないという条件を考えることにしました.その条件を
満たすためには,座標や速度を微小量だけずらさなくてはならないということになります.
次のように考えると分かりやすいでしょう.本来時間  がたった分だけ進んでいるはずなのに,運動の出発する
時刻をそれだけ遅らせたのだから,その分だけ運動は遅れているはずです.
がたった分だけ進んでいるはずなのに,運動の出発する
時刻をそれだけ遅らせたのだから,その分だけ運動は遅れているはずです.  は微小量だから,その間の
質点の速度の変化は無視できるでしょう.よって,
は微小量だから,その間の
質点の速度の変化は無視できるでしょう.よって,
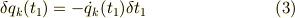
となります.マイナスになっているのは遅れていることを表すためです. 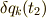 も同様に考えて,
も同様に考えて,
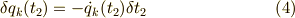
となります.
では,式(2)を計算していきます.微小量について2次以上の項は無視していきましょう.まずは,ラグランジアンをテイラー展開します.
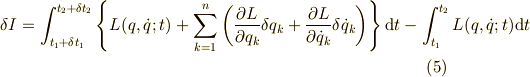
次に,微小量を表す項については積分区間を微小に変化させても,その変化分は2次以上の微小量となるので積分区間の微小変化は 無視します.

では,これを計算していきましょう.第1項では,積分区間をうまく入れ替えて次のように出来ます.
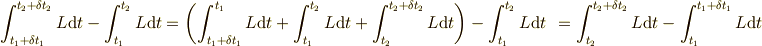
このようにすれば,微小区間での積分は
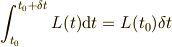
という式を使って展開することが出来ます.
また,運動の両端の変分は式(3),(4)で表せることと,ラグランジュの運動方程式が成立することは分かっているということに
注意してください.これで 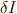 が次のように計算できます.
が次のように計算できます.
![\displaystyle\delta I&=\left(\int_{t_2}^{t_2+\delta t_2}L\mathrm{d}t-\int_{t_1}^{t_1+\delta t_1}L\mathrm{d}t\right)+\left[\sum_{k=1}^{n}{\partial L\over\partial\dot{q}_k}\delta q_k\right]_{t_1}^{t_2}+\int_{t_1}^{t_2}\sum_{k=1}^{n}\left({\partial L\over\partial q_k}-{\mathrm{d}\over\mathrm{d}t}{\partial L\over\partial\dot{q}_k}\right)\delta q_k\mathrm{d}t\\&=\{L(t_2)\delta t_2-L(t_1)\delta t_1\}+\sum_{k=1}^{n}\{p_k(t_2)\delta q_k(t_2)-p_k(t_1)\delta q_k(t_1)\}\\&=L(t_2)\delta t_2-L(t_1)\delta t_1+\sum_{k=1}^{n}\{-p_k(t_2)\dot{q_k}(t_2)\delta t_2+p_k(t_1)\delta q_k(t_1)\delta t_1\}\\&=\left\{\sum_{k=1}^{n}p_k(t_1)\dot{q}_k(t_1)-L(t_1)\right\}\delta t_1-\left\{\sum_{k=1}^{n}p_k(t_2)\dot{q}_k(t_2)-L(t_2)\right\}\delta t_2 \tag{7}](./5200d5820ab7ed712bb1ddc09c2bd203.png)
なんだか, ネーターの定理 と同じような形になりましたね.式変形の途中で一般化運動量の定義を使って式を簡単にしました.
ここで,エネルギーの関数 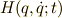 を次のように定義してみることにしましょう.
を次のように定義してみることにしましょう.
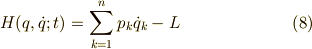
このとき,  は
は  を使って次のようにかけます.
を使って次のようにかけます.
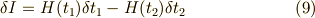
これは,時間の並進移動について作用 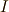 が不変のとき,
が不変のとき,  (ただし
(ただし  は
微小な定数)として
は
微小な定数)として 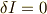 だから
だから

となります.つまり,式(8)で定義されるエネルギーは作用 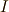 が時間について並進対称性を持つときに保存則が生じることが分か
りました.
が時間について並進対称性を持つときに保存則が生じることが分か
りました.
さて,最初に私たちはエネルギーの性質として,単純な力学系では 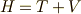 と書けることを要請していました.式(8)で定義した
エネルギー
と書けることを要請していました.式(8)で定義した
エネルギー 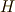 はこの性質を満たすのでしょうか?
はこの性質を満たすのでしょうか?
とにかく確認してみましょう.ラグランジアンを 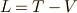 と定めます.直交座標系
と定めます.直交座標系 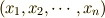 で考えると分かりや
すいでしょう.単純な力学系では運動エネルギー
で考えると分かりや
すいでしょう.単純な力学系では運動エネルギー 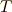 は
は 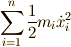 で表すことができ,
ポテンシャル
で表すことができ,
ポテンシャル  は位置のみの関数であったことを思い出してください.
は位置のみの関数であったことを思い出してください.
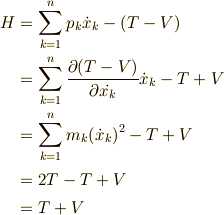
こうして,初めに考えた条件をすべて満たす物理量としてエネルギー 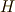 を定めることができましたね.でも,ラグランジアン
が
を定めることができましたね.でも,ラグランジアン
が 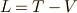 と表せないときにはどうなるのでしょうか?
と表せないときにはどうなるのでしょうか?
このときはニュートンの運動方程式を基礎とする立場から一般的にどう定義してよいかは分かりません.(もちろん,個々の 問題については物体に働く力を積分して求められることはあります.)その一方で変分原理やラグランジュの運動方程式を 基礎とする立場からは式(8)によってエネルギーを定義することができます.
それにしても,求める過程にせよ,作用の変分の形にせよ,エネルギーはまるで時間に共役な運動量みたいでしたね. 実際に相対性理論では,運動量の時間成分はエネルギーになりますし,量子論でもエネルギーと時間の間には密接な関係があります. 相対論や量子論とは一見関係なさそうな分野を学んでいるのに,そのことを示唆する結果が得られていくというのは, とても面白いですよね!