ダランベールの原理
静力学のときは,仮想仕事の原理によって複雑な拘束条件があるときでも,機械的に問題を処理できるようになりましたね. この便利さを静力学に留めておくのはもったいないです.そこで,この手法を動力学にも応用していきましょう.
ダランベールの原理とは
質点についてニュートンの運動方程式は次のように書けました.

質量 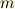 の質点が力
の質点が力 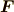 を受けて運動している様子を表してます.では,次のように書くとどうでしょう?
を受けて運動している様子を表してます.では,次のように書くとどうでしょう?

ただ移項しただけなんです.しかし,このように書くと,見かけ上 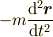 という力(慣性
抵抗と呼びます)が物体に働いて,力のつりあいが成り立っているとも見ることができますね.
つまり,動力学は静力学に帰着させることができるわけです.このことをダランベールの原理と呼んでいます.
名前の割りに,あっさりとした原理なんですね.
という力(慣性
抵抗と呼びます)が物体に働いて,力のつりあいが成り立っているとも見ることができますね.
つまり,動力学は静力学に帰着させることができるわけです.このことをダランベールの原理と呼んでいます.
名前の割りに,あっさりとした原理なんですね.
それでは,ダランベールの原理を用いて仮想仕事の原理を動力学に拡張しましょう.
まず,静力学における基本原理である仮想仕事の原理について簡単に述べておきます. 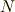 個の質点系について考えます.
各質点に働く力を
個の質点系について考えます.
各質点に働く力を 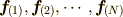 とおきます.
仮想仕事の原理とはこの質点系が静止しているための必要十分条件が次式で表せるというものでした.
とおきます.
仮想仕事の原理とはこの質点系が静止しているための必要十分条件が次式で表せるというものでした.
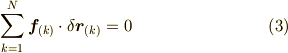
ただし, 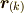 は
は 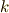 番目の質点の位置ベクトルで,
番目の質点の位置ベクトルで, 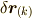 はその仮想変位をあらわすものとします.
はその仮想変位をあらわすものとします.
例えば,質点が静止しているのは質点に働く合力が 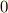 のときですね.つまり,仮想変位がすべて独立のときは式(3)は
次の式と同値になりますね.(
のときですね.つまり,仮想変位がすべて独立のときは式(3)は
次の式と同値になりますね.( 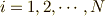 )
)

ただし,仮想変位がすべて独立じゃなければ式(3)と式(4)は同値ではありません.例えば,質点からなる剛体を考える場合, 力のつりあいと力のモーメントのつりあいさえ成り立てばよいので,式(4)では条件が厳しすぎますね.
つまり,さまざまな拘束条件が存在しても式(3)は成立するわけで,まさに原理と呼ぶのにふさわしいです.
以上が静力学についてでした.
次に動力学についてみていきましょう. 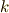 番目の質点が持つ運動量を
番目の質点が持つ運動量を 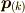 と定めます.式(2)を運動量を
用いて書けば,次のようになりますね.(
と定めます.式(2)を運動量を
用いて書けば,次のようになりますね.( 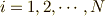 )
)

このとき,各質点は加速度運動を行います.しかし,慣性抵抗 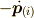 が働いて力のつりあいが再び成立
するんだ,と考えるのがダランベールの原理でした.
が働いて力のつりあいが再び成立
するんだ,と考えるのがダランベールの原理でした.
この見方に立つと式(3)は動力学の場合でも次の形で成立するはずです.
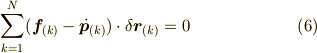
静力学のときと同じように,式(5)と式(6)は,仮想変位がすべて独立しているときは同値ですが,仮想変位が独立でないときは 同値ではありません.静力学のときと同じようにどんな拘束条件の下でも成り立つのは式(6)なのです. 式(6)はダランベールの原理を具体的に数式で表現したものですね.
座標変数を使った表現
今後,ベクトルをそのまま扱うことは少なく,座標系を適当に選んで座標変数について調べていくことが多くなります. そこで,座標変数のあらわし方について約束事を決めておきましょう.例として直交座標系を考えてみます.
前のセクションのように 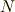 個の粒子を考える場合に,わざわざ
個の粒子を考える場合に,わざわざ 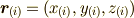 のように
三種類の文字を考えると,それぞれの文字について式を示さなくてはならず面倒です.そこで,次のように表してしまい
ましょう.
のように
三種類の文字を考えると,それぞれの文字について式を示さなくてはならず面倒です.そこで,次のように表してしまい
ましょう.
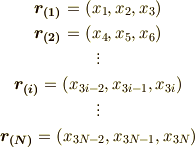
すべての変数を添字のみで区別するのですね.ここでは,直交座標変数を例にしましたが,より一般の座標系を選んだときや 物理量の成分を表示するときも同様にします.式(6)はこの記法を使えば次のように書けるでしょう.
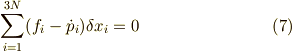
座標で表すときの表現にも慣れてくださいね.