行列式の導出
行列式の定義を見ると,どうしてこのような式を考え付いたのか想像しにくいですね. 行列式を使わずに連立1次方程式を解いて,行列式の導出を試みましょう.
3元連立1次方程式
一般の場合は式が複雑で考えにくいので,まず
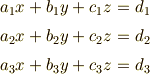
について考えましょう.  を求めるために
を求めるために 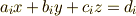 の辺々に
の辺々に 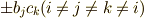 をかけた
をかけた
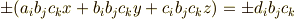
に対して,例えば
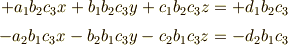
を辺々加算すると 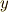 の係数が
の係数が 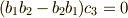 となります.また,
となります.また,
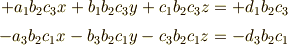
を加算すると  の係数が 0 になります.
の係数が 0 になります. 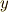 の係数には
の係数には 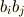 が,
が,  の係数には
の係数には
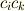 が含まれているのがポイントで,
が含まれているのがポイントで,
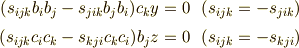
となるので,(とりあえず) 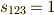 を初期値として符号
を初期値として符号 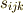 を
を
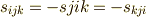 によって順次定めると
によって順次定めると
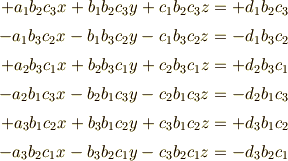
が得られ,総和をとると(結果的に) 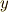 ,
,  の係数がいずれも 0 になることが分かります.
の係数がいずれも 0 になることが分かります.
置換による表現
集合  に対する1対1写像を置換といい,とくに
に対する1対1写像を置換といい,とくに
 の任意の2数だけを交換する置換を互換といいます.
の任意の2数だけを交換する置換を互換といいます.
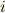 と
と 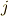 を交換する互換
を交換する互換 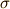 は
は
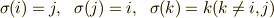 ですが,これを
ですが,これを 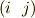 とかきます.任意の置換は互換の繰り返し(合成写像)で
表現できます.表現の仕方はいろいろありますが,置換を表現するのに必要な互換
の数は偶数か奇数かは変わりません.互換の数が偶数の置換を偶置換,奇数の置換を
奇置換といい,置換
とかきます.任意の置換は互換の繰り返し(合成写像)で
表現できます.表現の仕方はいろいろありますが,置換を表現するのに必要な互換
の数は偶数か奇数かは変わりません.互換の数が偶数の置換を偶置換,奇数の置換を
奇置換といい,置換 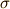 の符号を偶置換のときは
の符号を偶置換のときは 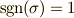 奇置換のときは
奇置換のときは 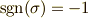 で定めます.
で定めます.
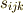 の
の 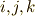 は互いに異なるので,置換
は互いに異なるので,置換 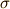 を用いて
を用いて
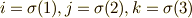 と表現でき,置換を用いると
と表現でき,置換を用いると 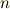 元連立1次方程式への拡張が容易になります.
元連立1次方程式への拡張が容易になります.
一般化準備として,まず
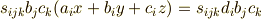
を置換を用いて書き換えましょう. 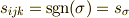 とし
とし
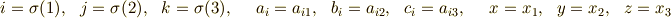
を代入した
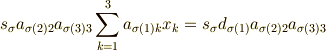
が 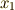 を求める式であることに注意.
を求める式であることに注意. 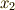 を求めるときの式は
を求めるときの式は
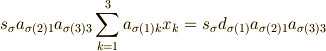
あるいは 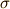 を変更した
を変更した
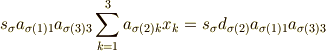
であり, 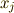 を求める式は
を求める式は
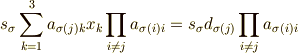
です.上式の 3 を 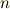 で置換し,
で置換し, 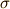 の定義域を
の定義域を  と考えれば,
そのまま一般の場合に適用できます.
と考えれば,
そのまま一般の場合に適用できます.
一般化
3 を 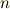 で置換し,
で置換し, 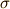 の定義域を
の定義域を  と考えても
と考えても 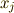 を同じ式で
求められることを確かめましょう.
を同じ式で
求められることを確かめましょう.
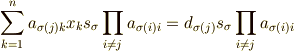
の 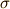 についての総和をとると,
についての総和をとると, 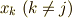 の係数は
の係数は
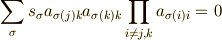
となります.ここで 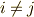 は
は 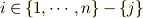 ,
, 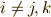 は
は
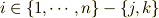 を意味します.上式が成立することは
を意味します.上式が成立することは
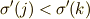 である任意の置換
である任意の置換 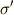 に対して置換
に対して置換
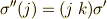 が存在して,
が存在して,
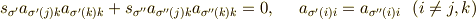
が成立するので, 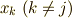 の係数である置換の総和を
の係数である置換の総和を 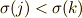 である置換の総和とそうでない置換の総和に分けると,これらの総和が相殺することから分かります.
である置換の総和とそうでない置換の総和に分けると,これらの総和が相殺することから分かります.
補遺
(1)発見的に考えるには対象を簡単化して見易い記号を使うこと.最初から
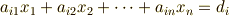
で考えようとすると無用な複雑さで思考が妨げられます.
(2)「3元連立1次方程式」では 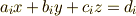 に
に 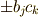 を
天下り的にかけましたが,
を
天下り的にかけましたが,
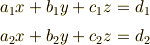
から  を消去すると
を消去すると
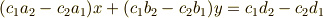
が得られ,同様に
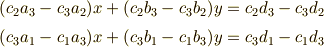
も成立するので, 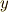 の係数に注目して
の係数に注目して
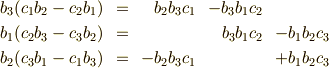
から,加重加算によって 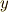 の係数を にできることが分かります.行列式で表すと
の係数を にできることが分かります.行列式で表すと
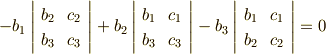
です.
(3)連立1次方程式
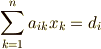
の解 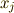 は
は
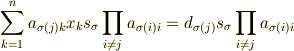
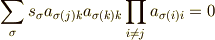
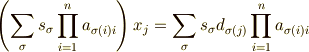
から 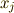 の係数が0でなければ一意に定まります.
の係数が0でなければ一意に定まります.
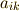 を
を 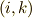 要素とする
要素とする 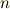 次正方行列
次正方行列 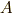 の行列式は
の行列式は
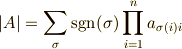
で定義されるので, 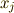 の係数が
の係数が 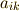 を
を 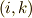 要素とする
要素とする 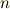 次正方行列
次正方行列 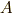 の
行列式であり,上式右辺は行列
の
行列式であり,上式右辺は行列 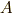 の
の 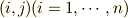 要素を
要素を 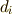 で置換した
行列の行列式になっていること(クラメルの公式)を確かめられます.
で置換した
行列の行列式になっていること(クラメルの公式)を確かめられます.