因数分解の一意性
多項式の因数分解について,次のような重要な定理があります.
theorem
多項式は全て,既約な多項式の積に因数分解でき,その分解の仕方はある体上で一意的です.
この定理の証明には,解析的な手法を必要とし,けっこう長いので省略します.中学校や高校で『次の式を因数分解しなさい』というような練習問題をやったと思いますが,上の定理の意味は『どんどん因数分解していけば,どこか決まったところでこれ以上因数分解できなくなるよ』ということです.経験上なんとなく定理の意味は明らかだと思います.学校でやった練習問題に決まった答えがあるのは,因数分解の仕方が一意的だからです.
また『ある体上で』という部分がとても重要です.例えば 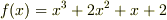 は
は 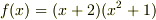 と因数分解できますが,有理数体上でこれ以上の因数分解はできません.しかし,もしも複素数体上で考えれば,さらに
と因数分解できますが,有理数体上でこれ以上の因数分解はできません.しかし,もしも複素数体上で考えれば,さらに 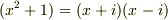 と因数分解できます.どちらにせよ,考えている体上では,既約多項式の積に因数分解できるのです.
と因数分解できます.どちらにせよ,考えている体上では,既約多項式の積に因数分解できるのです.
| [*] | 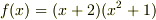 の因数分解は,中学校では の因数分解は,中学校では 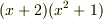 が答えでしたが,高校に行くと が答えでしたが,高校に行くと 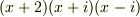 という分解も出てきました.『中学校ではまだ虚数を習ってないから』という,なんだか文部省の都合のような理由で数学の問題の答えが違うのはおかしいと思ったものですが,いまもう一度考えてみると,中学校の代数は実数体上に制限されており,高校の代数は複素数体上まで拡大されていたと言えるわけです.中学の教科書の巻頭に小さく『実数体上の因数分解だけを考えます』と書いておけば,高校の教科書と答えが違っても堂々と数学的に言い訳できたわけですね. という分解も出てきました.『中学校ではまだ虚数を習ってないから』という,なんだか文部省の都合のような理由で数学の問題の答えが違うのはおかしいと思ったものですが,いまもう一度考えてみると,中学校の代数は実数体上に制限されており,高校の代数は複素数体上まで拡大されていたと言えるわけです.中学の教科書の巻頭に小さく『実数体上の因数分解だけを考えます』と書いておけば,高校の教科書と答えが違っても堂々と数学的に言い訳できたわけですね. |
ただし,瑣末なことですが,定数倍だけ異なる多項式を別のものと考えれば,次の例のように無数の因数分解の仕方が可能になる場合もあります.今後,定数倍だけ異なる多項式は,基本的には同じものと考えます.
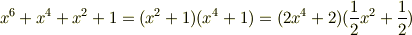
原始的な多項式
有理数体 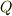 上の多項式
上の多項式 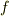 を考えます.
を考えます.
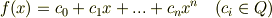
次の3つの条件を満たすとき 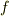 を 原始的 であると言います.
を 原始的 であると言います.
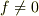
- 係数
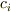 が全て整数である.
が全て整数である. - 係数
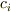 が全て互いに素である.
が全て互いに素である.
原始的な多項式には,次のような興味深い性質があります.
| [†] | また何だか変な用語が出てきましたが,原始的とは英語の 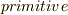 の訳です.原始と聞くと,どうも原始人・原始時代など,未開なイメージを想起させますから,あまり上手い訳語だとは思えませんが,日本語になかなかうまく対応する言葉がないのでしょう. の訳です.原始と聞くと,どうも原始人・原始時代など,未開なイメージを想起させますから,あまり上手い訳語だとは思えませんが,日本語になかなかうまく対応する言葉がないのでしょう. |
theorem
原始的な多項式同士の積は,やはり原始的になります.
proof
条件 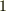 と
と 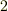 は明らかですから,条件
は明らかですから,条件 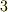 だけを確認すれば良いでしょう.二つの多項式を
だけを確認すれば良いでしょう.二つの多項式を 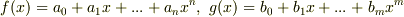 と置き,
と置き, 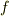 と
と 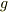 の積
の積 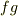 を考えます.いま仮に
を考えます.いま仮に 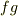 の係数が互いに素ではなく,公約数
の係数が互いに素ではなく,公約数 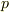 を持つとします.
を持つとします. 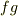 の
の 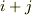 次の項の係数は
次の項の係数は 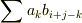 と表わされますので,これは
と表わされますので,これは 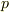 が
が 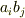 を割るという仮定に他なりません.しかし,
を割るという仮定に他なりません.しかし, 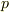 が
が 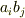 を割るならば,
を割るならば, 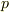 は
は 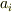 か
か 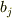 ,もしくはその両方を割るはずで( 既約と可約 参照),これは
,もしくはその両方を割るはずで( 既約と可約 参照),これは 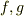 が原始的であるという条件に反します.よって
が原始的であるという条件に反します.よって 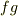 も原始的になります.■
も原始的になります.■
多項式 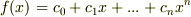 が
が 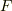 上で原始的ではないとすると,係数
上で原始的ではないとすると,係数 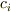 は最大公約元
は最大公約元  を持つはずです.その最大公約元を 内容 と呼び,
を持つはずです.その最大公約元を 内容 と呼び, 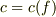 のように書きます.『原始的な多項式とは,
のように書きます.『原始的な多項式とは, 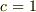 である多項式である』と言い換えることも出来ます.
である多項式である』と言い換えることも出来ます.
一般に,どのような多項式 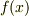 からでも,各係数を内容で割ることで原始的多項式
からでも,各係数を内容で割ることで原始的多項式 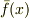 を作ることが出来ます.
を作ることが出来ます.
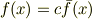
次の定理は「ガウスの補題」として知られている有名なものです.証明には原始的,内容など,いま出てきたばかりの概念をさっそく使います.
theorem
整係数の多項式は,整係数の多項式の積に因数分解できる場合のみ,有理数体 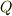 上で可約になります.
上で可約になります.
proof
整係数の多項式 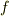 が
が 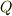 上
上 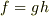 のように因数分解できるとします.
のように因数分解できるとします. 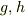 の内容を
の内容を 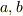 とすると,
とすると, 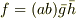 のように原始的な多項式
のように原始的な多項式 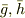 を使って
を使って 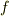 を表現できます.先ほどの定理により
を表現できます.先ほどの定理により 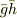 は原始的ですから,
は原始的ですから, 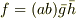 という表現は
という表現は 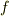 の因数分解になっています.
の因数分解になっています. 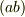 は
は 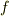 の内容で,明らかに整数です.逆に有理数体
の内容で,明らかに整数です.逆に有理数体 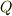 上で可約な多項式が因数分解できることは自明ですので,定理が示されます.■
上で可約な多項式が因数分解できることは自明ですので,定理が示されます.■
しばらく新しい定理や概念の説明ばかりが続きましたので,少し,しんどいく感じてきたかも知れません.覚えたことや分かったことを,少しずつ確認しながら先へ進むようにして下さい.ほとんどが多項式に関する話題でしたので,実際に二次方程式か何かの具体例を考えてみれば,新しい定理や概念の意味も納得いくと思います.もうしばらく代数方程式に関係した内容が続きます.