対称式・交代式と群
この記事では,対称式や交代式と対称群の関係を勉強します.いままでは図形の対称性が話題になっていましたが,ここでは方程式の対称性にします.対称性のあるところに群あり,です.
対称式と置換
多項式のうち,文字を入れ替えても式が変わらないものを 対称式 といいました.例えば,次式は対称式です.
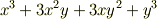
この 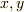 に互換
に互換 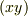 を作用させて,
を作用させて, 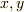 を入れ替えてしまうと次のようになります.
を入れ替えてしまうと次のようになります.
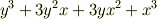
もちろん式は変わりません.次の式も対称式の例です.
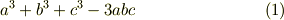
これに三次の置換を作用させると,次のような式を得るでしょう. もちろんどれも同じです.( 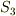 を思い出しましょう.)
を思い出しましょう.)
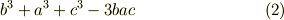
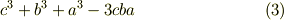
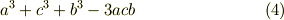
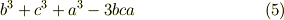
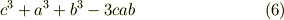
さて,  個の文字を含む多項式に対し,その多項式が対称式かどうかを判断するには,なにも
個の文字を含む多項式に対し,その多項式が対称式かどうかを判断するには,なにも  個の変数の置換を 全種類試す必要はありません .
個の変数の置換を 全種類試す必要はありません .
一般に,置換操作は全て互換の積で表わせるということでしたので,基本となる互換について対称式であることが分かれば,それらを合成した置換に対しても対称式であることが言えるはずです.
例えば,上の例で言えば,(1)〜(6)式全てを確認する必要はなく,3次の置換の基本となる 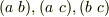 の三種の互換だけを調べれば良いわけです.さらに,この三つの互換は互いに独立ではなく,
の三種の互換だけを調べれば良いわけです.さらに,この三つの互換は互いに独立ではなく, 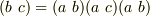 という関係 [*] で結ばれていますから,結局3つのうち二つを調べれば十分だということになります.
という関係 [*] で結ばれていますから,結局3つのうち二つを調べれば十分だということになります.
一般に,  個の文字の置換には
個の文字の置換には 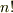 種類ありますが,
種類ありますが,  個の文字を含む多項式が対称式かどうかを確認するには,
個の文字を含む多項式が対称式かどうかを確認するには, 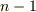 個の互換についてだけ調べれば良いことがわかります.随分手間が省けました.
個の互換についてだけ調べれば良いことがわかります.随分手間が省けました.
| [*] | このような関係を共役と言います.詳しくは 共役類 を参照してください. |
交代式と交代群
一方,文字を入れ替えると式全体の符号が変わってしまうような多項式を 交代式 と呼ぶのでした.例えば,次の式は交代式の例です. 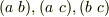 のどの互換を行っても,式の符号が変わることを確認してください.
のどの互換を行っても,式の符号が変わることを確認してください.

交代式に互換を一つ施すと符号が変わりますが,続けてもう一つ互換を行うと,結局符号は元に戻ります.つまり,偶数個の互換(偶置換)に対し,交代式は符号を変えないのです.符号が変わるのは,奇置換のときだけです.  個の文字からなる交代式の符号を変えない全ての置換の集まり(全ての偶置換)を n次の交代群 と呼びます.交代群の元は,全て偶置換です.
個の文字からなる交代式の符号を変えない全ての置換の集まり(全ての偶置換)を n次の交代群 と呼びます.交代群の元は,全て偶置換です.
交代群
交代群 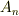 が群になることを確かめてみましょう.
が群になることを確かめてみましょう.
- 二つの偶置換
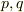 がそれぞれ単独に作用して交代式
がそれぞれ単独に作用して交代式 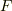 を変えないとき,これらを連続して作用させても符合は変わりません.すなわち
を変えないとき,これらを連続して作用させても符合は変わりません.すなわち 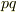 も偶置換であり,演算は閉じていると言えます.
も偶置換であり,演算は閉じていると言えます. - 結合則がなりたちます.
- 単位元が存在します.(何も順番を変えない置換です.)
- 逆元が存在することは次の証明のようにして示せます.
proof
ある互換 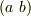 の逆元が
の逆元が  と示せることを使います.
と示せることを使います. 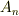 に属するある元
に属するある元 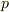 が互換の積として
が互換の積として 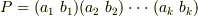 (
(  は偶数)と表わせるとすれば,この逆元は全部逆に並べ替えて
は偶数)と表わせるとすれば,この逆元は全部逆に並べ替えて 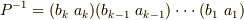 と書け,やはり偶数個の互換の積になります.よって逆元も偶置換で,交代群
と書け,やはり偶数個の互換の積になります.よって逆元も偶置換で,交代群 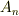 の中に存在します.■
の中に存在します.■
| [†] | 単位元は偶置換に含まれます.ある互換 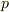 を二乗すると,一度入れ替えたものをもう一度入れ替えるのですから,何もしないことと同じになります.すなわち を二乗すると,一度入れ替えたものをもう一度入れ替えるのですから,何もしないことと同じになります.すなわち 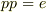 となり,単位置換は互換だと言えるのです. となり,単位置換は互換だと言えるのです. |
Important
n次の対称群のうち,偶置換だけから作った部分群を交代群と呼びます.
| [‡] | 奇置換だけを集めても群にはなりません.単位元が無いからです.ただし 半群 にはなります. |
交代群の位数
ある偶置換を  と置きます.
と置きます.  に,例えば互換
に,例えば互換 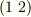 を一つ作用させると,これは奇置換になります.これを,偶置換に奇置換を対応させる変換
を一つ作用させると,これは奇置換になります.これを,偶置換に奇置換を対応させる変換 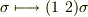 と見ると,任意の
と見ると,任意の  に対して必ず奇置換
に対して必ず奇置換 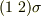 が一つだけ決まりますから『偶置換の個数
が一つだけ決まりますから『偶置換の個数 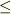 奇置換の個数』が言えます.
奇置換の個数』が言えます.
一方,任意の奇置換  に対して,同じ論法で一つだけ偶置換
に対して,同じ論法で一つだけ偶置換 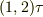 を対応させることができますから,やはり『奇置換の個数
を対応させることができますから,やはり『奇置換の個数 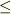 偶置換の個数』が言えます.
よって『偶置換の個数
偶置換の個数』が言えます.
よって『偶置換の個数  奇置換の個数』が導かれます. 偶置換の個数と奇置換の個数は常に等しい のです.
奇置換の個数』が導かれます. 偶置換の個数と奇置換の個数は常に等しい のです.
一般に  次の対称群について
次の対称群について 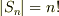 が言えましたので,上の結果より,交代群の位数はそのちょうど半分だと言えます.
が言えましたので,上の結果より,交代群の位数はそのちょうど半分だと言えます.
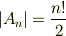
補足:基本対称式
対称式には色々なものがありますが,特にその基本となるのが,基本対称式と言われるものです.  種類の文字
種類の文字 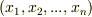 から,異なる
から,異なる  個の文字を取り出して作りうる積の総和を,
個の文字を取り出して作りうる積の総和を,  次の 基本対称式
次の 基本対称式 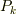 と呼びます.
と呼びます.
実際に例を見れば,すぐに意味が分かると思います.例えば 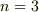 の場合は,次の三種類です.
の場合は,次の三種類です.
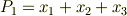
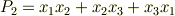

一方,  個の文字
個の文字 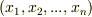 から選びうる,異なる
から選びうる,異なる 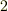 個の文字の差を全て掛け合わせたものを
個の文字の差を全て掛け合わせたものを  次の 最簡交代式
次の 最簡交代式 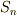 と呼びます.
と呼びます.
例えば 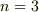 の場合は次のものです.
の場合は次のものです.
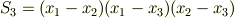
基本対称式や最簡交代式は,これ以降の群の理論には直接必要な話題ではありませんが,知っておいても損はないでしょう.方程式論で,また出てきます.一般に,全ての対称式は,基本対称式を組み合わせ,ただ一通りに表現できること,全ての交代式は,最簡交代式と対称式の積で表現できることが知られています.(この証明は 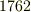 年,ウェアリング(
年,ウェアリング(  )によって与えられました.とても重要な定理ですが,ここでは証明しません.)
)によって与えられました.とても重要な定理ですが,ここでは証明しません.)