累開冪拡大とガロア群の関係
方程式の可解性を考える準備は,いよいよ大詰めです.累開冪拡大体の列と,ガロア群の関係を明らかにします.この記事の最初で,後の議論のために ラグランジェのリゾルベント と言われる量を導入します.後半で,ガロアの定理の証明に決定的に大事になる定理を証明します.(この定理は,ガロアの定理のための補題というよりは,それ自体でとても重要な定理だと思います.)気合を入れていきましょう.
ラグランジェのリゾルベント
まず,ラグランジェのリゾルベントと言われる量を導入します.ラグランジェのリゾルベントとは, 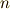 次方程式
次方程式  に対し,その解
に対し,その解 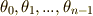 と,
と, 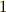 の
の 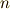 乗根の一つ
乗根の一つ 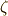 を,次のように順番に掛け合わせて足し合わせた量です.
を,次のように順番に掛け合わせて足し合わせた量です.
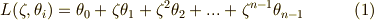
式 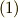 を念頭に,
を念頭に, 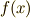 を体
を体 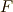 上の代数方程式だとし,拡大体
上の代数方程式だとし,拡大体 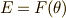 を考えます.いま, ガロア群が巡回群
を考えます.いま, ガロア群が巡回群 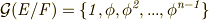 だとすると( この仮定が重要! ),解
だとすると( この仮定が重要! ),解 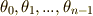 は
は 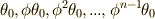 のように,
のように, 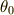 と
と 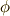 だけを使って書き換えることができます.(ただし,順番も同順とは限りません.)簡単のため,
だけを使って書き換えることができます.(ただし,順番も同順とは限りません.)簡単のため, 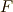 は
は 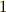 の
の 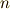 乗根
乗根 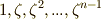 を含み,
を含み, 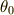 を単に
を単に 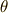 と書くことにすれば,式
と書くことにすれば,式 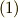 を次のように書き換えることができます.
を次のように書き換えることができます.
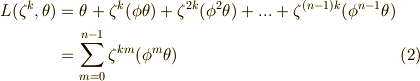
後で,この形でラグランジェのリゾルベントを利用します.また,ここでは仮に,  の
の 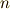 乗根
乗根 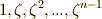 は,
は, 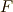 に含まれるとしておきます.(このため,
に含まれるとしておきます.(このため,  と考えます.)式
と考えます.)式 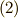 で両辺の総和を取ってみます.
で両辺の総和を取ってみます.
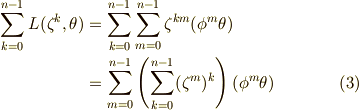
式  の右辺の括弧部分は,
の右辺の括弧部分は, 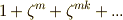 のように等比級数の和ですから,公式通りに
のように等比級数の和ですから,公式通りに 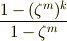 のように表現できますが,これは
のように表現できますが,これは 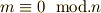 の場合に
の場合に 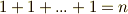 となり,それ以外の場合には
となり,それ以外の場合には 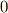 になります.
になります.
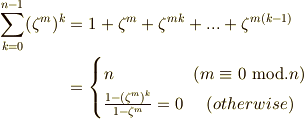
そこで,式  の
の  で生き残るのは,
で生き残るのは, 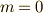 の場合だけなので,
の場合だけなので,  を考えると,式
を考えると,式  は次のように変形できます.
は次のように変形できます.
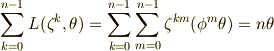
式  より,
より, 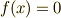 の解
の解 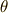 を次のように表現することが出来ます.これが,ラグランジェのリゾルベントを使った方程式の解の表現で,このようにして方程式の解を表す方法を ラグランジェの方法 と呼びます.
を次のように表現することが出来ます.これが,ラグランジェのリゾルベントを使った方程式の解の表現で,このようにして方程式の解を表す方法を ラグランジェの方法 と呼びます.

| [*] | これは,ラグランジェ(  )が提案した方程式の解法で,ラグランジェの方法と呼ばれています.ここまでの議論は,ガロア群が巡回群である,という仮定に基づいていますが(もう一度確認してみて下さい),これがもし巡回群でないと,式 )が提案した方程式の解法で,ラグランジェの方法と呼ばれています.ここまでの議論は,ガロア群が巡回群である,という仮定に基づいていますが(もう一度確認してみて下さい),これがもし巡回群でないと,式  によって簡単に方程式の解を示すことは出来ません.つまり,ガロア群が巡回群かどうか,というのがこの方法のポイントになってきます.ラグランジェは,まだ群論さえなかった時代に,既に巡回群に似た概念に到達し,それが方程式の可解性の要点であることを見抜いていました.ガロアも,まずラグランジェの著作を読み,ガロア群が巡回群になることと方程式の可解性の関係に気づき,そこから数日間のうちにガロア理論を完成させたと言います.ラグランジェの業績あってのガロア理論と言えそうです. によって簡単に方程式の解を示すことは出来ません.つまり,ガロア群が巡回群かどうか,というのがこの方法のポイントになってきます.ラグランジェは,まだ群論さえなかった時代に,既に巡回群に似た概念に到達し,それが方程式の可解性の要点であることを見抜いていました.ガロアも,まずラグランジェの著作を読み,ガロア群が巡回群になることと方程式の可解性の関係に気づき,そこから数日間のうちにガロア理論を完成させたと言います.ラグランジェの業績あってのガロア理論と言えそうです. |
もう一つ,重要な関係式を導いておきます.式 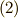 の両辺に
の両辺に 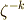 を掛けてみます.
を掛けてみます.
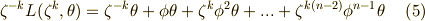
右辺第一項を, 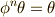 ,
, 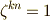 であることを使って,少し強引ですが
であることを使って,少し強引ですが 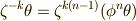 と変形すれば,式
と変形すれば,式 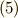 を次のように変形できます.(二行目から三行目は,単に順番を見やすいように並べ替えただけです.)
を次のように変形できます.(二行目から三行目は,単に順番を見やすいように並べ替えただけです.)
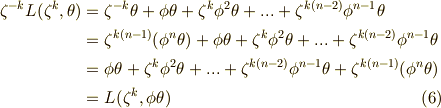
よって,次の関係式が得られました.
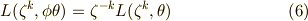
また, 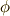 が
が  を不動に保つことを考えると,
を不動に保つことを考えると,  が言えますから,式
が言えますから,式 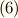 とまとめて,次の関係を得ます.
とまとめて,次の関係を得ます.
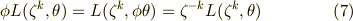
さらに, 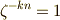 を使って,式
を使って,式 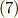 から次式を導くことが出来ます.
から次式を導くことが出来ます.

最後のところでは, 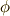 が準同型写像であること,つまり一般に
が準同型写像であること,つまり一般に 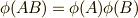 を満たすことを利用しています.式
を満たすことを利用しています.式 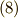 の最初と最後を比べて見れば,
の最初と最後を比べて見れば, 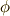 が
が 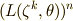 を不動に保つということが分かります.
を不動に保つということが分かります.
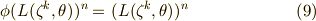
ラグランジェのリゾルベントの導入が長くなりましたが,ここまでの議論を使って,次に大事な定理を証明します.
定理
theorem
体 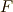 のガロア拡大
のガロア拡大 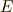 を考えます.もしガロア群
を考えます.もしガロア群 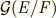 が可換群(または巡回群)ならば,
が可換群(または巡回群)ならば, 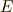 は
は 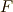 の開冪拡大だと言えます.
の開冪拡大だと言えます.
この定理は非常に重要で,これによって開冪拡大の列とガロア群の列が関係づけられます.有限巡回群は可解群だと言えましたので(すでに こちら で証明しました), 定理の可解群という部分を有限巡回群と読み換えても良いです.可解群という言葉に触れずに巡回群だけで説明してある教科書もあり,どちらでも良いと思います.
以下は,この定理の証明です.
特殊な場合
まず,  として,
として, 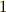 の
の 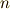 乗根
乗根  を
を 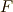 が含む特殊な場合を考えます.
が含む特殊な場合を考えます.
式 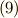 より,
より, 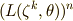 の形で表わされる数(
の形で表わされる数( 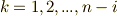 の
の 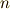 個あるので,
個あるので,  と名づけておきます)は,
と名づけておきます)は, 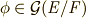 によって不動に保たれます.同じ議論が
によって不動に保たれます.同じ議論が 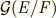 の他の元にも成り立ちますから,結局,
の他の元にも成り立ちますから,結局,  は
は 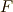 の元であるということが分かります.いま,
の元であるということが分かります.いま,  上の方程式
上の方程式 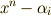 による分離拡大体を
による分離拡大体を 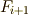 と定義することで,累開冪拡大体の列を考えることができます.
と定義することで,累開冪拡大体の列を考えることができます.

こ方程式 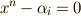 の解ということは,
の解ということは, 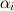 の
の 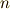 乗根を全て含むことになりますが,
乗根を全て含むことになりますが, 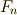 は全ての
は全ての  の
の 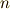 乗根を漏れなく含むことになりますので,結局,ラグランジェのリゾルベントの各項を全て含むことが示せます.これより,次の関係が言えます.
乗根を漏れなく含むことになりますので,結局,ラグランジェのリゾルベントの各項を全て含むことが示せます.これより,次の関係が言えます.

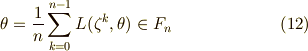
これより, 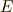 は
は 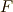 の累開冪拡大であることが示されました.■
の累開冪拡大であることが示されました.■
一般の場合
まず特殊な場合として, 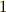 の
の 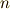 乗根が全て
乗根が全て 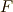 に含まれる場合について,定理を示しましたが,定理は
に含まれる場合について,定理を示しましたが,定理は 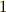 の
の 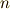 乗根が
乗根が 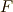 に含まれない場合に対しても拡張することが出来ます.
に含まれない場合に対しても拡張することが出来ます.
まず 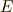 は,
は, 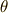 を解とする
を解とする 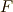 上の方程式
上の方程式 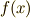 の最小分解体になっており,ガロア拡大であることを確認しましょう.(最小分解体は,常にガロア拡大でした.)これに対し,
の最小分解体になっており,ガロア拡大であることを確認しましょう.(最小分解体は,常にガロア拡大でした.)これに対し, 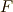 上の方程式
上の方程式 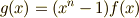 と,
と, 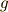 の最小分解体
の最小分解体 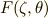 を考えてみます.これもガロア拡大です.このとき,
を考えてみます.これもガロア拡大です.このとき,  は
は 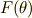 のガロア拡大でもある,ということも言え,
のガロア拡大でもある,ということも言え, 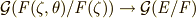 なる準同型写像を決めることが出来ます.このような準同型写像を
なる準同型写像を決めることが出来ます.このような準同型写像を 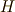 とすると,
とすると, 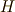 の作用する被写像元を,
の作用する被写像元を, 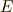 に制限することが出来ます.これを
に制限することが出来ます.これを 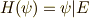 のように書きます.(
のように書きます.( 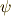 は
は 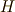 が作用するのですから,少なくとも
が作用するのですから,少なくとも 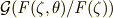 の元で,つまり
の元で,つまり 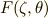 の自己同型写像です.
の自己同型写像です. 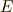 を
を  の部分体と考えることが出来ますから,
の部分体と考えることが出来ますから, 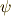 として
として 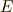 に制限されたものを考えることは可能なわけです.)さらに,この
に制限されたものを考えることは可能なわけです.)さらに,この 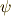 として,一対一写像のものを決めることも出来ますから,も
として,一対一写像のものを決めることも出来ますから,も 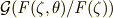 と
と 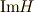 に同型写像を決めることが出来ます.
に同型写像を決めることが出来ます. 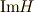 は
は 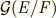 の部分群なので巡回群ですので,これより
の部分群なので巡回群ですので,これより 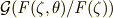 も巡回群だと言うことが出来ます.また,
も巡回群だと言うことが出来ます.また, 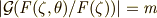 (
( 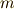 は
は  を割り切る適当な整数)と置くことが出来ます.結局,『
を割り切る適当な整数)と置くことが出来ます.結局,『 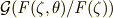 は位数
は位数 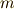 の巡回群である』ことが分かり, さらに
の巡回群である』ことが分かり, さらに 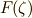 は
は 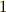 の
の 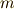 乗根
乗根 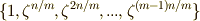 を全て含むのですから,ここから先は前セクションで証明した『特殊な場合』の証明に帰着させることが出来ます.すなわち,
を全て含むのですから,ここから先は前セクションで証明した『特殊な場合』の証明に帰着させることが出来ます.すなわち, 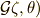 は
は 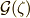 の累開冪拡大であり,
の累開冪拡大であり, 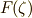 が
が 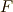 の累開冪拡大であることを考えれば,
の累開冪拡大であることを考えれば,  という,前セクションと同じ結論を得ることが出来ます.■
という,前セクションと同じ結論を得ることが出来ます.■