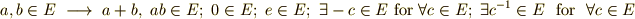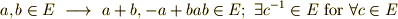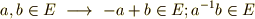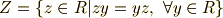部分環・部分体
環や体の部分集合で,同じ演算に関して同じ構造を持つものを部分環,部分体と呼びます.
Important
環 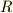 の部分集合
の部分集合 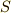 が,
が, 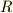 と同じ加法と乗法について環になるとき,
と同じ加法と乗法について環になるとき, 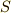 を部分環と呼びます.
を部分環と呼びます.
つまり 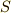 に属する任意の元
に属する任意の元 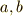 について,
について, 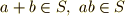 がなりたつということです.部分体の定義も同様です.
がなりたつということです.部分体の定義も同様です.
Important
体 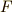 の部分集合
の部分集合 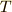 が,
が, 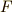 の加法と乗法について体になるとき,
の加法と乗法について体になるとき, 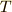 を部分体と呼びます.
を部分体と呼びます.
簡単ですね.
| [*] | 環 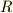 自身および零元だけからなる集合 自身および零元だけからなる集合 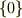 はいつでも部分環になります.これを自明な部分環と呼びます.(群で,単位元と群自身はいつでも自明な部分群になることを思い出してください.)体でもやはり,零元だけからなる集合と体自身は,いつでも自明な部分体になります. はいつでも部分環になります.これを自明な部分環と呼びます.(群で,単位元と群自身はいつでも自明な部分群になることを思い出してください.)体でもやはり,零元だけからなる集合と体自身は,いつでも自明な部分体になります. |
例1
整数環 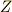 は複素数環
は複素数環 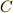 (
( 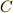 は複素数体でもある)の部分環になっています.
は複素数体でもある)の部分環になっています.
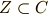
また複素数体 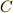 ,実数体
,実数体 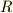 ,有理数
,有理数 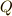 の間には次のような包含関係があります.実数体は複素数体の部分体,有理数体は実数体の部分体になっています.
の間には次のような包含関係があります.実数体は複素数体の部分体,有理数体は実数体の部分体になっています.
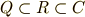
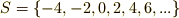 は部分環になります.
は部分環になります. 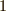 が含まれませんから,乗法の単位元はありません.
が含まれませんから,乗法の単位元はありません.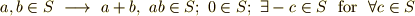
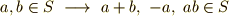

 について,以下の4つの文・式は
について,以下の4つの文・式は