簡約法則
半群が群になる条件を考えます.
半群が群になるとき
半群の定義から明らかなように,もし半群が単位元と逆元を持てば,群になると言えるでしょう.つまり,半群の任意の元  に対して次の条件を満たすような元
に対して次の条件を満たすような元  ,
, 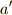 が存在することが条件になります.
が存在することが条件になります.




式 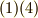 は左からの作用,式
は左からの作用,式 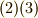 は右からの作用に対応しています.しかし,この4つの条件は,さらに次のように集約することが出来ます.半群の元
は右からの作用に対応しています.しかし,この4つの条件は,さらに次のように集約することが出来ます.半群の元 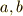 に対し,もし次の二つの条件を満たす元
に対し,もし次の二つの条件を満たす元 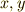 が半群の中に存在するば,半群は群になります.
が半群の中に存在するば,半群は群になります.


式 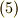 で
で 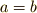 と置けば
と置けば  は
は  のことを意味してますし,
のことを意味してますし, 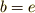 と置けば
と置けば  は
は 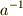 のことを意味します.つまり式
のことを意味します.つまり式 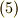 だけで,式
だけで,式 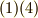 をカバーできます.同様に右作用に関しては式
をカバーできます.同様に右作用に関しては式 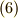 で,式
で,式 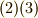 をカバーできます.式
をカバーできます.式 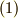 〜
〜 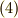 を,式
を,式 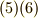 にまとめることが出来ました.
にまとめることが出来ました.
この条件をもう少しじっくり見てみましょう.式 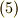 を『半群がもし群になるならば,
を『半群がもし群になるならば, 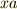 という元が一つ群の中に決まる』と読むことも出来ます.そこで
という元が一つ群の中に決まる』と読むことも出来ます.そこで 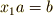 を満たす
を満たす 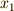 と,
と, 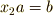 を満たす
を満たす 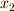 が存在する場合,
が存在する場合, 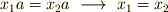 がなりたたなければなりません.右作用も同様で,式
がなりたたなければなりません.右作用も同様で,式 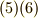 は,次の二式がなりたつ条件だと書き換えることができます.
は,次の二式がなりたつ条件だと書き換えることができます.
これを 簡約法則 と呼びます.何のことはない,『同じものがあれば両辺から割って簡単にできるよ』というだけのことです. 半群は,簡約法則を満たすとき群になります .
簡約法則の一例
有限群の元の結合について,総当り表にして元の結合をみる群表というものがありました.例えば, クラインの四元群 に出てきた群表は次のようなものでした.
| e | p | q | r | |
|---|---|---|---|---|
| e | e | p | q | r |
| p | p | e | r | q |
| q | q | r | e | p |
| r | r | q | p | e |
この群表をよく見ると,同一の縦のライン,もしくは横のラインに同じ元は一度しか出てこないことが分かります.
| [*] | このような文字の並びをラテン方陣と言います.魔方陣に少し似ていますが,魔方陣は同一列のある数字の和が等しくなるように数字を配列したものです.ラテン方陣はそのような計算には関係なく,単に同じ文字は同じ列に一度しか出ない,という少し簡単な決まりに基づく方陣です.数字を並べる魔方陣に対して,文字を並べるという意味でラテン(アルファベットのことをラテン文字と呼びます)方陣と言うのです.数独(SUDOKU)という,空欄に数字を埋めていくゲームがありますが,数独はラテン方陣になっています. |
なぜ同じ元が一度しか出てこないのか,ということは簡約法則を使えばたちどころに分かります(群は半群でもあるので,もちろん簡約法則を満たします).
例えば,クラインの四元群の表で,上から二列目の横の段で 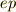 の欄と
の欄と 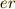 の欄に同じ元が出てくるとしましょう.つまり
の欄に同じ元が出てくるとしましょう.つまり 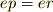 ということです.するとこれは,簡約法則より
ということです.するとこれは,簡約法則より 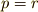 となって
となって 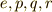 が異なるという前提に矛盾します.縦の列についても同じ論法がなりたち,群表の同一な列には同じ元は二度は出てこないことが示せました.
が異なるという前提に矛盾します.縦の列についても同じ論法がなりたち,群表の同一な列には同じ元は二度は出てこないことが示せました.
群は確かに簡約法則を満たしています.
theorem
半群は,簡約法則を満たすとき群になります.

