半群・モノイド
いままでは群ばかりを勉強してきましたが，他にもいろいろある代数構造を学ぶ手始めとして，半群を取り上げます．半群は，いますぐ使うわけではありませんが，群を見つめなおすのにも良い視点になることでしょう．
半群の定義
次のような条件を満たす集合を 半群 と呼びます．
- 結合法則を満たす演算が定義されている．
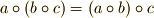
半群の定義はたったこれだけです．群の定義と比べると，単位元や逆元の存在が言われていません．半群は名前の通り，群よりも弱い構造だということができます．
モノイド
ついでにもう一つ， モノイド と呼ばれる代数構造を紹介します．
- 結合法則を満たす演算が定義されている．
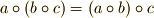
- 単位元がある．
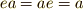
モノイドは，半群よりも単位元の存在を要請している点で強い構造ですが，逆元の存在は言われていませんので，群よりは弱い構造だと言えます．ちょうど半群と群の中間の構造です．モノイドは『単位元を持つ半群』だとも言えるし，『群から逆元の条件を外したもの』とも考えられます．
例１
正の整数全体は，加法に関して半群になります．結合則を満たし，正の整数と正の整数の和も正の整数となるからです．
単位元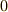 
は『正の整数』には含まれませんので，モノイドにはなりません．もし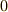， を含めればモノイドになります．逆元(つまり負の整数)は存在しませんので，群にはなりません．
例２
集合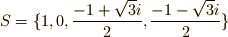 
はモノイドになっています．普通の意味の掛け算に対して 
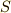の元は閉じていますし，結合則も満たします．また，単位元 
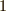も存在するのでモノイドです．しかし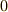， を掛けてしまうと逆元が定義できませんので逆元は無く，群にはなりません．
| [*] | このように，零元を含む集合に乗法を入れると，通常は逆元が定義できなくなりますので群にはならず，多くの場合は半群やモノイドになります．また，微分演算子が元として入っていたりすると，元の結合によって微分が行われてしまい，逆に戻すことが出来なくなります(例えば定数を微分したら全て 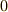になってしまいます)．このような事情で，解析や計算機理論など，微分の関係する分野で半群がよく使われるようです． |
半群が群になるとき
半群には半群で，半群論という世界があり，この記事で半群の性質を紹介することは出来ません．この記事のポイントは，代数構造の強弱(包含関係)を理解することです．
半群は今までで出てきた代数構造の中で一番弱いものですから，それよりも強い構造を全て含みます．モノイドは単位元を持つ半群，群は単位元と逆元を持つ半群である，と見ることが出来ますから，半群になりたつ性質は全てモノイドや群にもなりたつわけです．
今後，群よりもさらに強い構造である，環，体などを勉強していきますが，より弱い代数構造でなりたった性質は，より強い構造でもなりたつ，というのが大事な視点です．いままで群論で勉強してきた定理や概念を，そっくりそのまま体論や環論で使えるのです．
| [†] | あまりにも弱い構造(一番弱い構造は『何の演算も定義されていない単なる集合』ということになるでしょう)は，漠然としすぎていて何の役にたつのか分かりませんし，あまりにも強い構造はルールが複雑すぎて特殊な用途にしか使えません．たいていの代数の教科書が群論から始まっているのは，群の代数構造の強さが，一般性と応用性のどちらから見ても勉強を始めるのにちょうど良いからだと思われます．群から始めて，環，体，リー環，束など，より強い代数構造の勉強へ進む方向性と，半群やモノイドという，より弱く一般的な構造の勉強へと進む方向性との両方が考えられます．うーん，どれも面白そうです． |
もう一つ重要なのは，群よりも弱い構造である半群に，いったいどうのような条件が付加されたときに群になるか，ということです．一般に，何か代数構造を持つ集合があったとき，その集合がさらに付加的な条件を満たせば，さらに強い構造へと昇格できます(半群が単位元を持てばモノイドになりますし，モノイドが逆元を持てば群になります)．
半群やモノイドが群になる条件を，次の 簡約法則 で検討します．
