累開冪拡大体の列
体 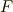 上の代数方程式
上の代数方程式 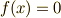 が 代数的に解ける とは,
が 代数的に解ける とは, 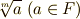 の形の数を
の形の数を 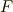 に添加して作った拡大体の中に,全ての解が納まることを意味します.『代数的に代数方程式を解く』とは,加減乗除の四つと,開冪(
に添加して作った拡大体の中に,全ての解が納まることを意味します.『代数的に代数方程式を解く』とは,加減乗除の四つと,開冪( 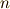 乗根を求める操作)の五つを使って,方程式を変形することですが,ここで係数体の拡大を伴うのは冪根だけだからです.(もっとも,体の定義は加減乗除について閉じているということでしたから,当たり前のことを言っているだけとも思えます. 代数方程式の性質 も参照してみて下さい.) 分離拡大体 で考えた言葉を使えば,
乗根を求める操作)の五つを使って,方程式を変形することですが,ここで係数体の拡大を伴うのは冪根だけだからです.(もっとも,体の定義は加減乗除について閉じているということでしたから,当たり前のことを言っているだけとも思えます. 代数方程式の性質 も参照してみて下さい.) 分離拡大体 で考えた言葉を使えば, 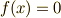 の最小分解体が,次のような体の昇鎖列のどこかに含まれているということになります.
の最小分解体が,次のような体の昇鎖列のどこかに含まれているということになります.
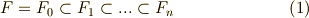
基礎体は 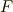 で,各次数の拡大体は
で,各次数の拡大体は 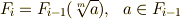 の形で表わされるものとします.式
の形で表わされるものとします.式 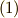 のように冪根を付け足すことで作る拡大体を 累開冪拡大 (
のように冪根を付け足すことで作る拡大体を 累開冪拡大 ( 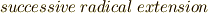 )と呼ぶことにします.
この記事では,このような累開冪拡大体の昇鎖列を考えます.まず次の定理が言えます.
)と呼ぶことにします.
この記事では,このような累開冪拡大体の昇鎖列を考えます.まず次の定理が言えます.
lemma
体 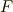 上の代数方程式
上の代数方程式 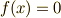 が開冪で解けるための必要十分条件は,解を全て含む累開冪ガロア拡大体が存在することです.
が開冪で解けるための必要十分条件は,解を全て含む累開冪ガロア拡大体が存在することです.
proof
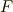 上の代数方程式
上の代数方程式 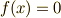 の最小分解体を少なくとも含む体として,累開冪拡大
の最小分解体を少なくとも含む体として,累開冪拡大 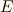 が存在するとすると,
が存在するとすると, 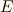 の共役体もまた累開冪拡大になるはずです.そこで,共役体を全て併せた体もまた累開冪拡大になります.分離かつ正規な拡大体をガロア拡大と呼んだのですから,結局,そのような体はガロア拡大になります.逆に,累開冪ガロア拡大でなく,方程式の解を全て含む体は考えられません.■
の共役体もまた累開冪拡大になるはずです.そこで,共役体を全て併せた体もまた累開冪拡大になります.分離かつ正規な拡大体をガロア拡大と呼んだのですから,結局,そのような体はガロア拡大になります.逆に,累開冪ガロア拡大でなく,方程式の解を全て含む体は考えられません.■
つまり,根体の昇鎖列は,ガロア拡大の昇鎖列の中に埋め込むことが出来るということが分かりました.また,次の定理も言えます.(定理と証明が細々と続いて申し訳ありません.方程式の可解性を議論する武器が出揃うまで,もう少しです(>_<).ガンバロウ)
theorem
式 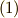 の拡大列で,
の拡大列で, 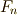 が
が 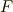 のガロア拡大ならば,中間体
のガロア拡大ならば,中間体 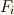 も全てガロア拡大になります.
も全てガロア拡大になります.
proof
まず,式 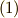 とは別に,ガロア拡大の列
とは別に,ガロア拡大の列 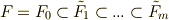 を考えます.
を考えます. 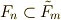 とします.この二つの拡大列を比べていきましょう.まず,
とします.この二つの拡大列を比べていきましょう.まず,  は自明です.
は自明です. 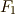 は
は 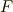 上の代数方程式
上の代数方程式  の最小分解体になっており,これはガロア拡大の定義に他ならないからです( 参考 ).次に,ガロア群
の最小分解体になっており,これはガロア拡大の定義に他ならないからです( 参考 ).次に,ガロア群 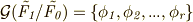 を考えます.定義通り,
を考えます.定義通り, 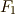 上の方程式
上の方程式 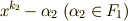 の最小分解体を
の最小分解体を  とするとき,
とするとき, 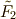 を
を  上の方程式
上の方程式 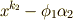 の最小分解体,
の最小分解体, 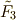 を
を 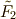 上の方程式
上の方程式 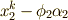 の最小分解体・・・と順次決め,最後に
の最小分解体・・・と順次決め,最後に 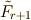 を
を 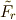 上の方程式
上の方程式 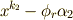 の最小分解体と決めます.さて,最後に考えた
の最小分解体と決めます.さて,最後に考えた 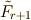 は,方程式
は,方程式 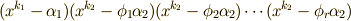 の最小分解体になっており,各
の最小分解体になっており,各 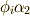 は,
は, 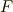 を不動に保つというガロア群の定義より,全て
を不動に保つというガロア群の定義より,全て 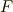 の元ですから,
の元ですから, 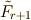 は
は 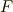 のガロア拡大になっています.
のガロア拡大になっています.  は
は 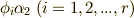 のどれかと等しいはずですから,
のどれかと等しいはずですから, 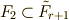 が言えます.同じ議論を繰り返し,今度はガロア群
が言えます.同じ議論を繰り返し,今度はガロア群 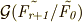 と
と  を使うことで,
を使うことで, 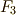 を含むガロア拡大列を考えることが出来ます.このようにして,
を含むガロア拡大列を考えることが出来ます.このようにして, 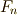 を含むまでガロア拡大列を伸ばすことが出来ます.■
を含むまでガロア拡大列を伸ばすことが出来ます.■
徐々に,代数方程式の解という話(最小分離体などの拡大体列)と,ガロア拡大,ガロア群,可解群といった話がつながってきました.色々な名前が出てきていますし,実際,同じ定理にも色々な表現方法がありますので,教科書によって少し違う表現や証明をしている場合があります.正規拡大体,正規部分群などの基本となる概念をきちんと理解しているか,もう一度理解を整理しておきましょう.上の定理を使って,次の定理を示すことも出来ます.
corollary
体 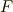 に累開冪拡大体の列
に累開冪拡大体の列  があり,
があり, 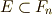 であるとき,
であるとき, 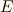 も
も 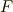 の開冪拡大体です.
の開冪拡大体です.
証明は,同じようにやればよいので自分で考えてみて下さい.